I haven't systematically studied JAVA yet, so this note studies the shortest path problem of graph in data structure C language version.
route
Considering the weighted digraph, the sum of the weights of the edges on a road force (only considering a simple path) is defined as the path length or weighted path length of the path
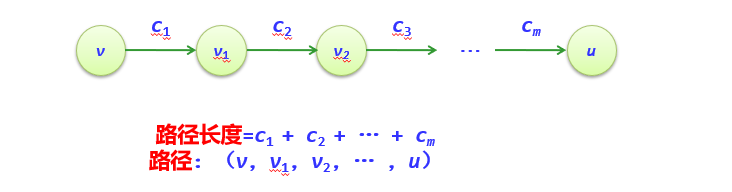
There may be more than one path from the source point to the end point. The path with the shortest path length is called the shortest path. In many cases, the shortest path of two vertices is not necessarily unique, but the shortest path length must be unique.
Shortest path algorithm
Dijkstra algorithm
Problem: given a weighted digraph g and source point v, find the shortest path from V to other vertices in G, and limit the weight on each edge to be greater than or equal to 0.
The single source shortest path problem can be solved by Dijkstra algorithm
Basic ideas
Let G=(V,E) be a weighted directed graph, and divide the vertex set V in the graph into two groups:
——The first group is the set of vertices for which the shortest path has been found (represented by S. at the beginning, there is only one source point in S. after each shortest path v,..., u is found, u is added to the set s until all vertices are added to s, and the algorithm ends)
——The second group is the set of other vertices (represented by U) for which the shortest path is not found. The vertices of the second group are added to S in the order of increasing the length of the shortest path

Specific steps
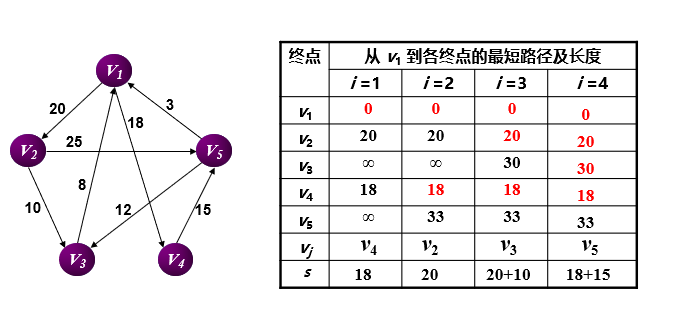
(1) Initialization: S only contains the source point, that is, S={v}, and the shortest path of v is 0. U contains other vertices except v, and the distance of vertex i in U is the weight on the edge (if v and I have edges < v, I >) or infinite (if I is not the edge adjacent contact of v).
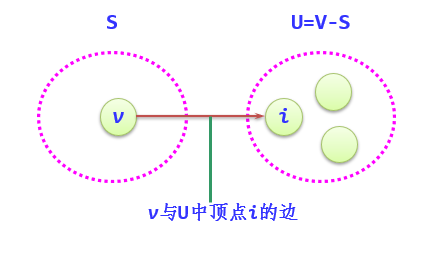
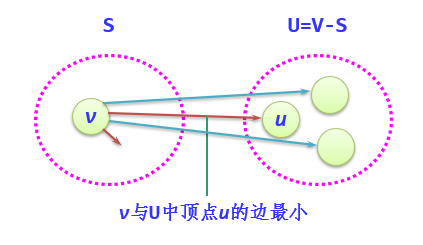
(2) select a vertex u with the smallest distance v from u and add u to S (the selected distance is the shortest path length from v to U).
(3) Take u as the newly considered middle point, modify the shortest path length of each vertex j in U: if the shortest path length (passing through vertex u) from source point v to j (j belongs to U) is shorter than the original shortest path length (not passing through vertex u), modify the shortest path length of vertex j.
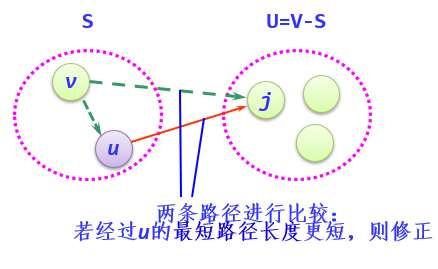
(4) repeat (2) and (3) until all vertices are included in S.
Algorithm design
How to store the shortest path length:
Stored in a one-dimensional array dist [j]. By default, dist [j] represents the shortest path length from the source point to v ertex j.
How to store the shortest path:
There are n-1 shortest paths from the source point to other vertices. One shortest path is represented by a one-dimensional array, and all n-1 shortest paths can be stored by a two-dimensional array path [] [].
The corresponding Dijkstra algorithm is as follows:
void Dijkstra(MatGraph g,int v) //Dijkstra algorithm
{ int dist[MAXV],path[MAXV];
int S[MAXV]; //S[i]=1 indicates that vertex I is in s, and S[i]=0 indicates that vertex I is in U
int Mindis,i,j,u;
bool flag;
for (i=0;i<g.n;i++)
{ dist[i]=g.edges[v][i]; //Distance initialization
S[i]=0; //S [] empty
if (g.edges[v][i]<INF) //Path initialization
path[i]=v; //When there is an edge from vertex v to vertex i, the previous vertex of vertex I is v
else
path[i]=-1; //When there is no edge from vertex v to vertex i, the previous vertex of vertex I is - 1
}
disp(dist,path,g.n);
printf("(%d)Set vertex%d Add to S aggregate\n",++count,v);
S[v]=1;path[v]=0; //The source point number v is placed in S
for (i=0;i<g.n-1;i++) //Loop until the shortest path of all vertices is found
{ Mindis=INF; //Mindis sets the initial value of the maximum length
for (j=0;j<g.n;j++) //Select the vertex u that is not in S (i.e. in U) and has the minimum shortest path length
if (S[j]==0 && dist[j]<Mindis)
{ u=j;
Mindis=dist[j];
}
printf(" reach U Smallest vertex in%d\n",u);
printf("(%d)Set vertex%d Add to S aggregate\n",++count,u);
S[u]=1; //Add vertex u to S
flag=false;
for (j=0;j<g.n;j++) //Modify the shortest path of vertices that are not in S (that is, in U)
if (S[j]==0)
{
if (g.edges[u][j]<INF)
{
flag=true;
printf(" Consider vertices%d Adjacency point of%d:",u,j);
if (dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
printf("Modify its shortest path length dist[%d]by%d,",j,dist[j]);
path[j]=u;
printf("Modify shortest path path[%d]by%d\n",j,u);
}
else
printf("vertex%d The shortest path length of has not been modified\n",j);
}
}
if (!flag)
printf(" vertex%d There are no adjacent points not considered(Do not modify)\n",u);
disp(dist,path,g.n);
}
Dispath(g,dist,path,S,v); //Output shortest path
}The Dispath() function that outputs the shortest path of a single source is as follows:
void Dispath(MatGraph g,int dist[],int path[],int S[],int v)
//Outputs all shortest paths from vertex v
{ int i,j,k;
int apath[MAXV],d; //Store a shortest path (reverse) and the number of vertices
for (i=0;i<g.n;i++) //Loop outputs the path from vertex v to i
if (S[i]==1 && i!=v)
{ printf(" From vertex%d To vertex%d The path length of is:%d\t Path is:",v,i,dist[i]);
d=0; apath[d]=i; //Add end point on path
k=path[i];
if (k==-1) //No path
printf("no path\n");
else //Output the path when it exists
{ while (k!=v)
{ d++; apath[d]=k;
k=path[k];
}
d++; apath[d]=v; //Add start point on path
printf("%d",apath[d]); //Output starting point first
for (j=d-1;j>=0;j--) //Then output other vertices
printf(",%d",apath[j]);
printf("\n");
}
}
}Regardless of the output of the path, the time complexity of Dijkstra algorithm is O(n^2), where the number of vertices in n graph
Floyd algorithm
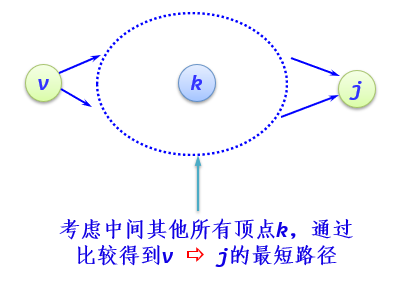
Problem: for a directed graph whose edge weight is greater than 0, for each vertex I is not equal to j, find the shortest path and the shortest path length between vertex i and vertex J.
The multi-source shortest path problem can be solved by Floyd algorithm
Algorithm idea
Suppose that the directed graph G = (V, e) is stored by adjacency matrix. Set A two-dimensional array A to store the shortest path length between the current vertices, and the component A [i] [j] represents the shortest path length from the current vertices I to j.
Recursion produces a matrix sequence: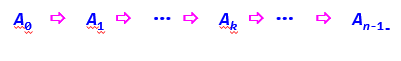
A [i] [J]: the shortest path length where the vertex number on the path from I to j is not greater than k
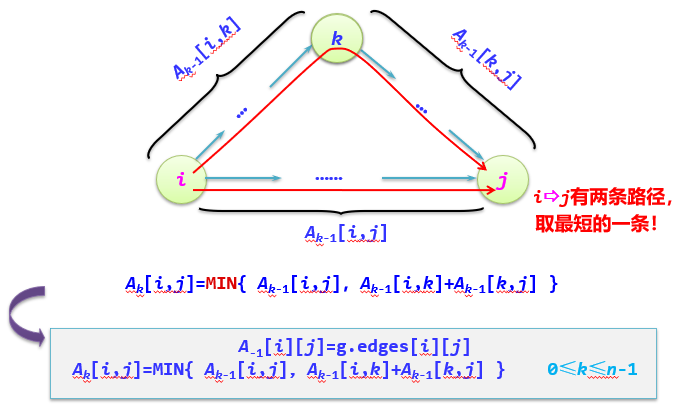
Algorithm design
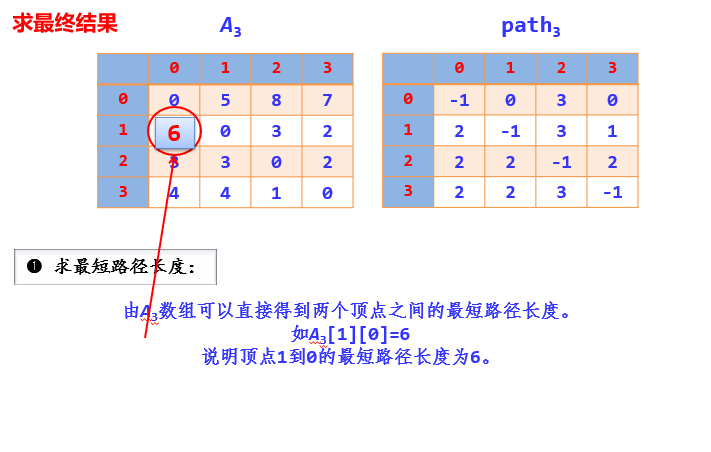
Store the shortest path length with two-dimensional array A:
A [i] [J] represents the shortest path length from I to j after considering vertices 0 ~ k.
The last a [i] [j] of the array represents the shortest path length from the final I to j.
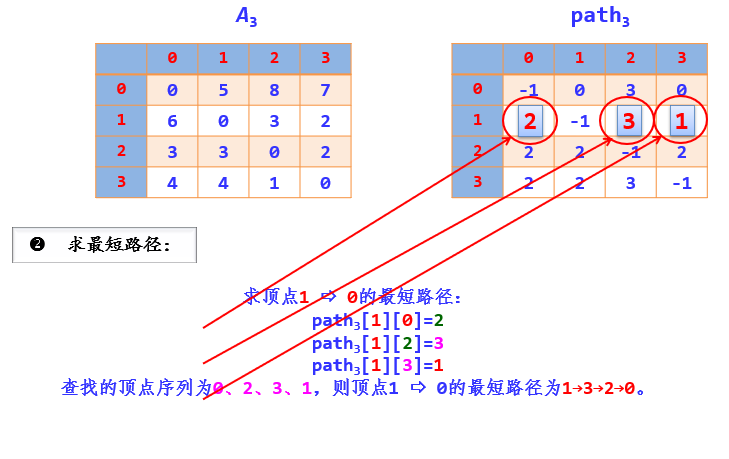
Use the two-dimensional array path to store the shortest path:
Path [i] [J] represents the shortest path from I to j after considering vertices 0 ~ k.
The last path [i] [j] of the array represents the shortest path from the final I to j.
The corresponding Floyd algorithm is as follows:
void Floyd(MatGraph g) //Floyd algorithm
{ int A[MAXV][MAXV],path[MAXV][MAXV];
int i,j,k;
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
{ A[i][j]=g.edges[i][j];
if (i!=j && g.edges[i][j]<INF)
path[i][j]=i; //When vertices i to j have edges
else
path[i][j]=-1; //When vertices i to j have no edges
}
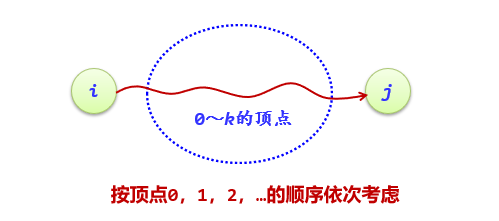
for (k=0;k<g.n;k++) //Look at all vertices in turn
{ for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
if (A[i][j]>A[i][k]+A[k][j])
{ A[i][j]=A[i][k]+A[k][j]; //Modify the shortest path length
path[i][j]=path[k][j]; //Modify shortest path
}
}
Dispath(g,A,path); //Output shortest path
}The Dispath() function that outputs the shortest path of multiple sources is as follows:
void Dispath(MatGraph g,int A[][MAXV],int path[][MAXV])
{ int i,j,k,s;
int apath[MAXV],d; //Store the middle vertex (reverse) of a shortest path and the number of vertices
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
{ if (A[i][j]!=INF && i!=j) //If there is a path between vertices i and j
{ printf(" from%d reach%d The path to is:",i,j);
k=path[i][j];
d=0; apath[d]=j; //Add end point on path
while (k!=-1 && k!=i) //Add middle point on path
{ d++; apath[d]=k;
k=path[i][k];
}
d++; apath[d]=i; //Add start point on path
printf("%d",apath[d]); //Output starting point
for (s=d-1;s>=0;s--) //Middle vertex on output path
printf(",%d",apath[s]);
printf("\t Path length is:%d\n",A[i][j]);
}
}
}Without considering the path output, the time complexity of Floyd algorithm is O(n^3), where n is the number of vertices in the graph.
compare
| algorithm | purpose | Time complexity | characteristic |
|---|---|---|---|
| Dijkstra | Single source shortest path | O(n^2) | Not suitable for negative weight |
| Floyd | Multi source shortest path | O(n^3) | Not suitable for negative weight circuit |