Java sorting

catalogue

Java sorting

preface

1, Simple sort

1. Bubble sorting

2. Select Sorting

3. Insert sort

2, Advanced sorting

1. Hill sort

2. Merge and sort

3. Quick sort

3, Stability of sorting

preface

Sorting is a very common requirement. It provides some data elements and sorts them according to certain rules. The sorting algorithms are described in turn below. The content comes from the dark horse programmer.

1, Simple sort

1. Bubble sorting

Code implementation:

package sort;

import javax.sound.midi.Soundbank;
import java.awt.image.ImageFilter;
import java.util.Arrays;

/**
 * @Date: 2022/1/6 - 01 - 06 - 14:04
 * @Description:
 */
public class Bubble {
    public static void sort(Comparable[] a){
        for (int i = a.length-1; i >0 ; i--) {
            for (int j = 0; j <i ; j++) {
                if (greater(a[j],a[j+1])){
                    exch(a,j,j+1);
                }
            }
        }
    }
    private static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w)>0;
    }
    private static void exch(Comparable[] a,int i,int j){
        Comparable t=a[i];
        a[i]=a[j];
        a[j]=t;
    }

    public static void main(String[] args) {
        Integer[] a={4,5,2,3,7,8,0};
        Bubble.sort(a);
        System.out.println(Arrays.toString(a));
    }
}

2. Select Sorting

Code implementation:

package sort;

import java.util.Arrays;

/**
 * @Date: 2022/1/6 - 01 - 06 - 14:51
 * @Description:
 */
public class Selection {
    public static void sort(Comparable[] a){
        for (int i = 0; i <a.length-1; i++) {//Because there is no need to select the remaining element, I < a.length-1
            //Cycle the value of the minimum index in turn
            int min=i;
            for (int j = i+1; j <a.length ; j++) {
                if (greater(a[min],a[j])){//Compare the value with the minimum index. If the minimum index is large, exchange the subscript value
                    min=j;
                }
            }
            exch(a,min,i);//Swap element positions after exchanging Subscripts
        }
    }
    private static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w)>0;
    }
    private static void exch(Comparable[] a,int i,int j){
        Comparable t=a[i];
        a[i]=a[j];
        a[j]=t;
    }
    public static void main(String[] args) {
        Integer[] a={4,5,2,3,7,8,0};
        Bubble.sort(a);
        System.out.println(Arrays.toString(a));
    }
}

Time complexity analysis of selective sorting: selective sorting uses a double-layer for loop, in which the outer loop completes data exchange and the inner loop completes data comparison, So we count the data exchange times and data comparison times respectively: data comparison times: (n-1) + (n-2) + (n-3) ++ 2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2; Data exchange times: n-1 time complexity: n ^ 2 / 2-N / 2 + (n-1) = N^2/2+N/2-1; According to the large o derivation rule, the highest order term is retained and the constant factor is removed. The time complexity is O(N^2);

3. Insert sort

As shown in the figure:

Code implementation:

package sort;

/**
 * @Date: 2022/1/6 - 01 - 06 - 15:30
 * @Description:
 */
public class Insertion {
    public static void sort(Comparable[] a){
        for(int i=1;i<a.length;i++){//Traverse from the second element
            for(int j=i;j>0;j--){
                //Compare the value at index j with the value at index j-1. If the value at index j-1 is larger than the value at index j, exchange data. If it is not large, find the appropriate position and exit the loop;
                if (greater(a[j-1],a[j])){
                    exch(a,j-1,j);
                }else{
                    break;
                }
            }
        }
    }
    private static  boolean greater(Comparable v,Comparable w){
        return v.compareTo(w)>0;
    }
    private static void exch(Comparable[] a,int i,int j){
        Comparable temp;
        temp = a[i];
        a[i]=a[j];
        a[j]=temp;
    }
}

2, Advanced sorting

1. Hill sort

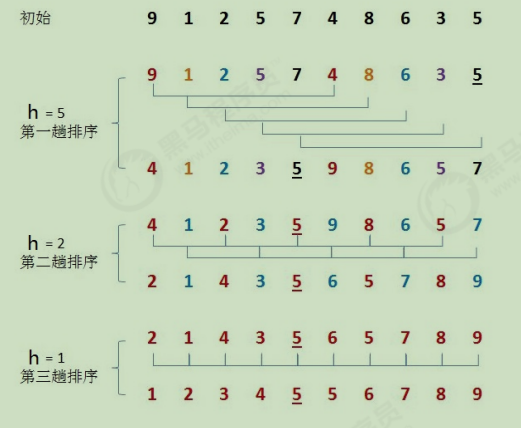
Code implementation:

package sort;

/**
 * @Date: 2022/1/6 - 01 - 06 - 15:44
 * @Description:
 */
public class Shell {
    public static void sort(Comparable[] a){
        //1. Determine the initial value of the growth amount h according to the length of array a;
        int h = 1;
        while(h<a.length/2){
            h=2*h+1;
        }
        //2. Hill sort
        while(h>=1){
            //sort
            //2.1. Find the element to insert
            for (int i=h;i<a.length;i++){
                //2.2 insert the elements to be inserted into the ordered sequence
                for (int j=i;j>=h;j-=h){
                    //The element to be inserted is a[j], compare a[j] and a[j-h]
                    if (greater(a[j-h],a[j])){
                        //Exchange element
                        exch(a,j-h,j);
                    }else{
                        //The element to be inserted has found the appropriate position and ends the loop;
                        break;
                    }
                }
            }
            //Decrease the value of h
            h= h/2;
        }
    }
    private static  boolean greater(Comparable v,Comparable w){
        return v.compareTo(w)>0;
    }
    private static void exch(Comparable[] a,int i,int j){
        Comparable temp;
        temp = a[i];
        a[i]=a[j];
        a[j]=temp;
    }
}

Hill sort and insert sort performance comparison test code:

public class SortCompare {
    //Call different test methods to complete the test
    public static void main(String[] args) throws Exception{
        //1. Create an ArrayList set and save the read integers
        ArrayList<Integer> list = new ArrayList<>();

        //2. Create a cache read stream BufferedReader, read data and store it in ArrayList;
        BufferedReader reader = new BufferedReader(new InputStreamReader(SortCompare.class.getClassLoader().getResourceAsStream("reverse_arr.txt")));
        String line=null;
        while((line=reader.readLine())!=null){
            //Line is a string. Convert line to Integer and store it in the collection
            int i = Integer.parseInt(line);
            list.add(i);
        }

        reader.close();


        //3. Convert the ArrayList set into an array
        Integer[] a = new Integer[list.size()];
        list.toArray(a);
        //4. Call the test code to complete the test
        //testInsertion(a);//37499 MS
        testShell(a);//30 ms
//        testMerge(a);//70 ms

    }

    //Test Hill sort
    public static void testShell(Integer[] a){
        //1. Get the time before execution
        long start = System.currentTimeMillis();
        //2. Execute algorithm code
        Shell.sort(a);
        //3. Get the time after execution
        long end = System.currentTimeMillis();
        //4. Calculate the execution time of the program and output it
        System.out.println("The execution time of Hill sort is:"+(end-start)+"millisecond");

    }

    //Test insert sort
    public static void testInsertion(Integer[] a){
        //1. Get the time before execution
        long start = System.currentTimeMillis();
        //2. Execute algorithm code
        Insertion.sort(a);
        //3. Get the time after execution
        long end = System.currentTimeMillis();
        //4. Calculate the execution time of the program and output it
        System.out.println("Insert sort execution time:"+(end-start)+"millisecond");
    }

    //Test merge sort
    public static void testMerge(Integer[] a){
        //1. Get the time before execution
        long start = System.currentTimeMillis();
        //2. Execute algorithm code
        Merge.sort(a);
        //3. Get the time after execution
        long end = System.currentTimeMillis();
        //4. Calculate the execution time of the program and output it
        System.out.println("The execution time of merge sort is:"+(end-start)+"millisecond");
    }

}

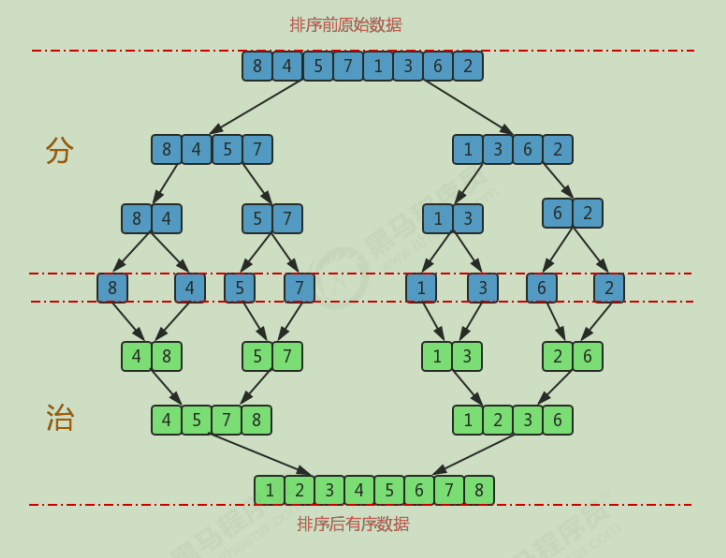
2. Merge and sort

Sorting principle:

        1. Split a set of data into two subgroups with equal elements as far as possible, and continue to split each subgroup until the number of elements in each subgroup after splitting is 1.

        2. Merging two adjacent subgroups into an ordered large group;

        3. Keep repeating the steps 2 Until there is only one group.

As shown in the figure:

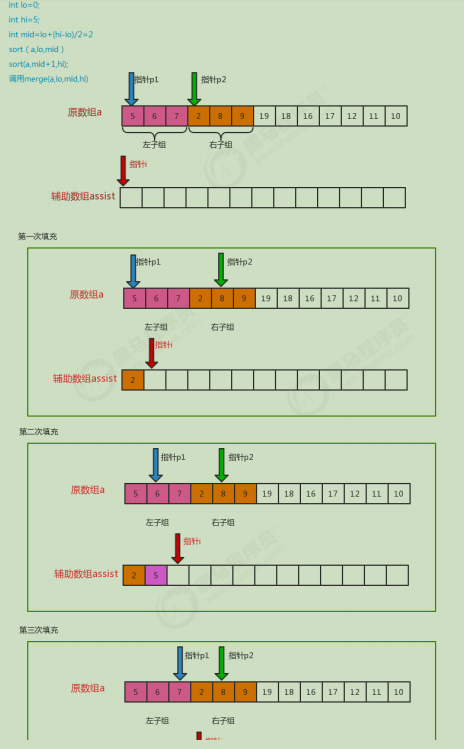
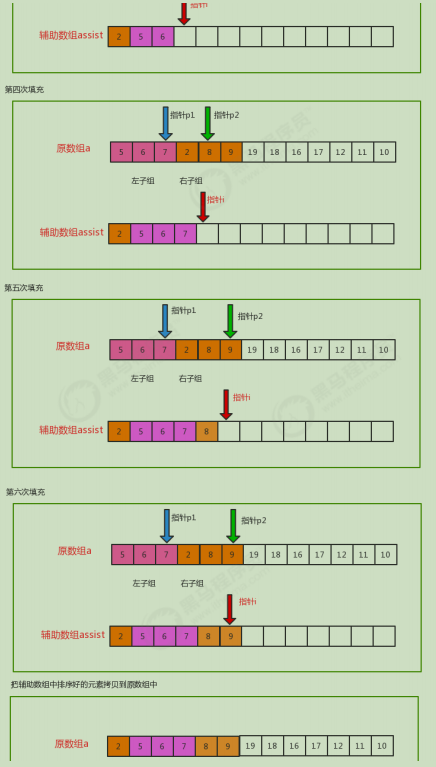
Filling principle: divide the original array into left subgroup and right subgroup. p1 pointer is the left subgroup pointer, p2 is the right subgroup pointer, and set i as the auxiliary array pointer. Compare the size of the element indicated by the current p1 and p2 pointers, and put the small one at the pointer i; Then move the p1,p2,i pointers backward to continue the comparison.

 

 

 

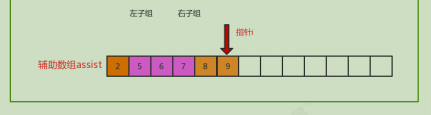
Code implementation:

package sort;

/**
 * @Date: 2022/1/7 - 01 - 07 - 10:14
 * @Description:
 */
public class Merge {
    //Auxiliary array required for merging
    private static Comparable[] assist;
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w)<0;
    }
    private static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
    public static void sort(Comparable[] a) {
        //1. Initialize auxiliary array assist;
        assist = new Comparable[a.length];
        //2. Define a lo variable and a hi variable to record the minimum index and the maximum index in the array respectively;
        int lo=0;
        int hi=a.length-1;
        //3. Call the sort overloaded method to sort the elements in array a from index lo to index hi
        sort(a,lo,hi);
    }
    private static void sort(Comparable[] a, int lo, int hi) {
        //Conduct safety verification;
        if (hi<=lo){
            return;
        }
        //The data between lo and hi are divided into two groups
        int mid = lo+(hi-lo)/2;//   5,9  mid=7
        //Sort each group of data separately
        sort(a,lo,mid);
        sort(a,mid+1,hi);
        //Then merge the data in the two groups
        merge(a,lo,mid,hi);
    }
    private static void merge(Comparable[] a, int lo, int mid, int hi) {
        //Define three pointers
        int i=lo;
        int p1=lo;
        int p2=mid+1;
        //Traverse, move the p1 pointer and p2 pointer, compare the value at the corresponding index, find the small one, and put it at the corresponding index of the auxiliary array
        while(p1<=mid && p2<=hi){
            //Compare the values at the corresponding index
            if (less(a[p1],a[p2])){
                assist[i++] = a[p1++];
            }else{
                assist[i++]=a[p2++];
            }
        }
        //Traversal. If the p1 pointer is not completed, move the p1 pointer in sequence and put the corresponding element at the corresponding index of the auxiliary array
        while(p1<=mid){
            assist[i++]=a[p1++];
        }
        //Traversal. If the p2 pointer is not completed, move the p2 pointer in sequence and put the corresponding elements at the corresponding index of the auxiliary array
        while(p2<=hi){
            assist[i++]=a[p2++];
        }
        //Copy the elements in the auxiliary array to the original array
        for(int index=lo;index<=hi;index++){
            a[index]=assist[index];
        }
    }
}

Merge sort time complexity analysis:

Merge sort is the most typical example of divide and conquer. In the above algorithm, for a[lo...hi] To sort, first divide it into a[lo...mid] and a[mid+1...hi] two parts, sort them separately through recursive calls, and finally merge the ordered sub arrays into the final sorting result. The exit of this recursion is that if an array can no longer be divided into two sub arrays, merge will be executed Merge. When merging, judge the size of elements and sort them. Use a tree view to describe merging, if an array has 8 Elements, then it will divide each time 2 Find the smallest subarray and split it log8 Times, the value is 3 So there are three trees layer , So top-down k Layer has 2^k Subarray, the length of each array is 2^(3-k) , merging requires at most 2^(3-k) Comparison. Therefore, the comparison times of each layer is 2^k * 2^(3-k)=2^3, that 3 The total number of layers is 3*2^3. Suppose the number of elements is n , then the number of times to split using merge sort is log2(n), So total log2(n) Layer, then use log2(n) Replace above 3*2^3 3 in According to the number of layers, the time complexity of merging and sorting is: log2(n)* 2^(log2(n))=log2(n)*n, According to big O The derivation rule ignores the base number, and the time complexity of final merging and sorting is O(nlogn)

Code tests are sorted as above.

3. Quick sort

Sorting principle:

        1. First, set a boundary value, and divide the array into left and right parts through the boundary value;

        2. Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, each element in the left part is less than Or equal to the boundary value, and all elements in the right part are greater than or equal to the boundary value;

        3. Then, the data on the left and right can be sorted independently. For the array data on the left, you can take another boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly.

        4. By repeating the above process, we can see that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the data of the left and right parts are sorted, the sorting of the whole array is completed

As shown in the figure:

Segmentation principle:

The basic idea of dividing an array into two subarrays:

1. Find a reference value and point to the head and tail of the array with two pointers respectively;

2. First, search for an element smaller than the reference value from the tail to the head, stop the search, and record the position of the pointer;

3. Then, search for an element larger than the reference value from the head to the tail, stop when the search is found, and record the position of the pointer;

4. Exchange the elements of the current left pointer position and the right pointer position;

5. repeat 2,3,4 Step until the value of the left pointer is greater than the value of the right pointer.

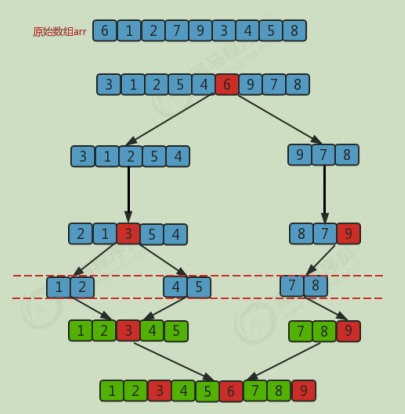
Code implementation:

package sort;

/**
 * @Date: 2022/1/7 - 01 - 07 - 10:36
 * @Description:
 */
public class Quick {
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }
    private static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
    public static void sort(Comparable[] a) {
        int lo = 0;
        int hi = a.length-1;
        sort(a,lo,hi);
    }
    private static void sort(Comparable[] a, int lo, int hi) {
        //Security verification
        if (hi<=lo){
            return;
        }
        //The elements from lo index to hi index in the array need to be grouped (left subgroup and right subgroup);
        int partition = partition(a, lo, hi);//Returns the index of the boundary value of the group, and the index after the boundary value position transformation
        //Order the left subgroup
        sort(a,lo,partition-1);
        //Order the right subgroup
        sort(a,partition+1,hi);
    }
    //Group the elements in array a from index lo to index hi, and return the index corresponding to the grouping boundary
    public static int partition(Comparable[] a, int lo, int hi) {
        //Determining the boundary value is the first element
        Comparable key = a[lo];
        //Define two pointers to point to the next position at the minimum index and the maximum index of the element to be segmented
        int left=lo;
        int right=hi+1;
        //segmentation
        while(true){
            //Scan from right to left, move the right pointer, find an element with small score boundary value, and stop
            while(less(key,a[--right])){
                if (right==lo){
                    break;
                }
            }
            //Scan from left to right, move the left pointer, find an element with a large score boundary value, and stop
            while(less(a[++left],key)){
                if (left==hi){
                    break;
                }
            }
            //Judge left > = right. If yes, it proves that the element scanning is completed and ends the cycle. If not, it can exchange elements
            if (left>=right){
                break;
            }else{
                exch(a,left,right);
            }
        }
        //Exchange the boundary value. right=left refers to the position
        exch(a,lo,right);
        //Finally, the boundary value can be returned
        return right;
    }

}

Difference between quick sort and merge sort:

Quick sort is another divide and conquer sorting algorithm. It divides an array into two sub arrays and sorts the two parts independently. Quick sort and merge sort are complementary: merge sort divides the array into two sub arrays, sorts them respectively, and merges the ordered sub arrays to sort the whole array. The way of quick sort is that when the two arrays are ordered, the whole array is naturally ordered. In merge sort, an array is equally divided into two parts. The merge call occurs before processing the whole array. In quick sort, the position of the split array depends on the content of the array, and the recursive call occurs after processing the whole array.

Quick sort time complexity analysis:

A quick sort of segmentation starts from both ends and searches alternately until left and right Therefore, the time complexity of the primary segmentation algorithm is O(n), However, the time complexity of the whole quick sort is related to the number of segmentation.

Optimal situation: the benchmark number selected for each segmentation just divides the current sequence equally.

If we regard the segmentation of an array as a tree, then the figure above is an illustration of its optimal situation, CO segmentation logn Therefore, the time complexity of quick sorting in the optimal case is O(nlogn);

Worst case: the benchmark number selected for each segmentation is the maximum number or the minimum number in the current sequence, so that each segmentation will have a subgroup, so the total will be segmented n Therefore, in the worst case, the time complexity of quick sort is O(n^2);

Average situation: the benchmark number selected for each segmentation is neither the maximum value nor the minimum value nor the median value. In this case, we can also prove by mathematical induction that the time complexity of quick sorting is O(nlogn). Because mathematical induction has a lot of mathematical related knowledge, it is easy to confuse us, Therefore, the time complexity of the average case is not proved here.

3, Stability of sorting

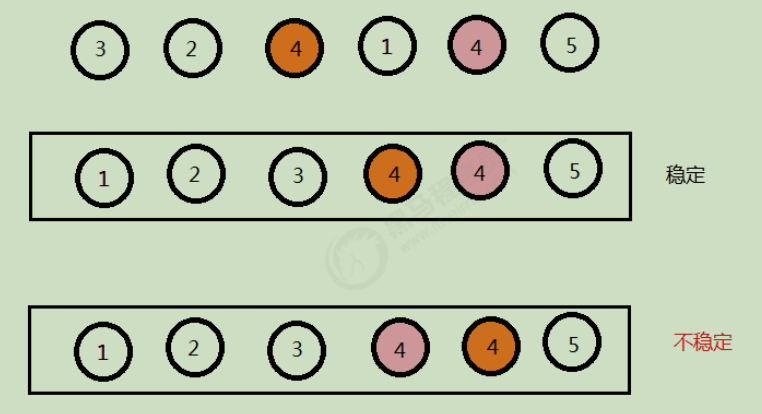
• Bubble sort: only when arr [i] > arr [i + 1], the positions of elements will be exchanged, and when they are equal, they will not be exchanged. Therefore, bubble sort is a stable sort algorithm.
• Selective sorting: selective sorting is to select the smallest current element for each position. For example, there is data {5 (1), 8, 5 (2), 2, 9}. The smallest element selected for the first time is 2, so 5 (1) will exchange positions with 2. At this time, the stability is destroyed when 5 (1) comes behind 5 (2). Therefore, selective sorting is an unstable sorting algorithm.
• Insertion sort: the comparison starts from the end of the ordered sequence, that is, the element to be inserted starts from the largest one that has been ordered. If it is larger than it, it will be inserted directly behind it. Otherwise, it will look forward until it finds the insertion position. If you encounter an element that is equal to the inserted element, put the element to be inserted after the equal element. Therefore, the sequence of equal elements has not changed. The order out of the original unordered sequence is the order after the order is arranged, so the insertion sort is stable.
• Hill sort: Hill sort sorts the elements according to the unsynchronized length. Although one insertion sort is stable and does not change the relative order of the same elements, in different insertion sort processes, the same elements may move in their own insertion sort, and finally their stability will be disturbed. Therefore, Hill sort is unstable.
• Merge sort: in the process of merge sort, only when arr [i] < arr [i + 1] will the position be exchanged. If the two elements are equal, the position will not be exchanged, so it will not destroy the stability. Merge sort is stable.
• Quick sort: quick sort requires a benchmark value. Find an element smaller than the benchmark value on the right side of the benchmark value, find an element larger than the benchmark value on the left side of the benchmark value, and then exchange the two elements. At this time, stability will be destroyed. Therefore, quick sort is an unstable algorithm.