preface
Binary search tree, also known as binary sort tree, is either an empty tree or a binary tree with the following properties:
- If its left subtree is not empty, the value of all nodes on the left subtree is less than that of the root node
- If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of the root node
- Its left and right subtrees are also binary search trees
You can do this:
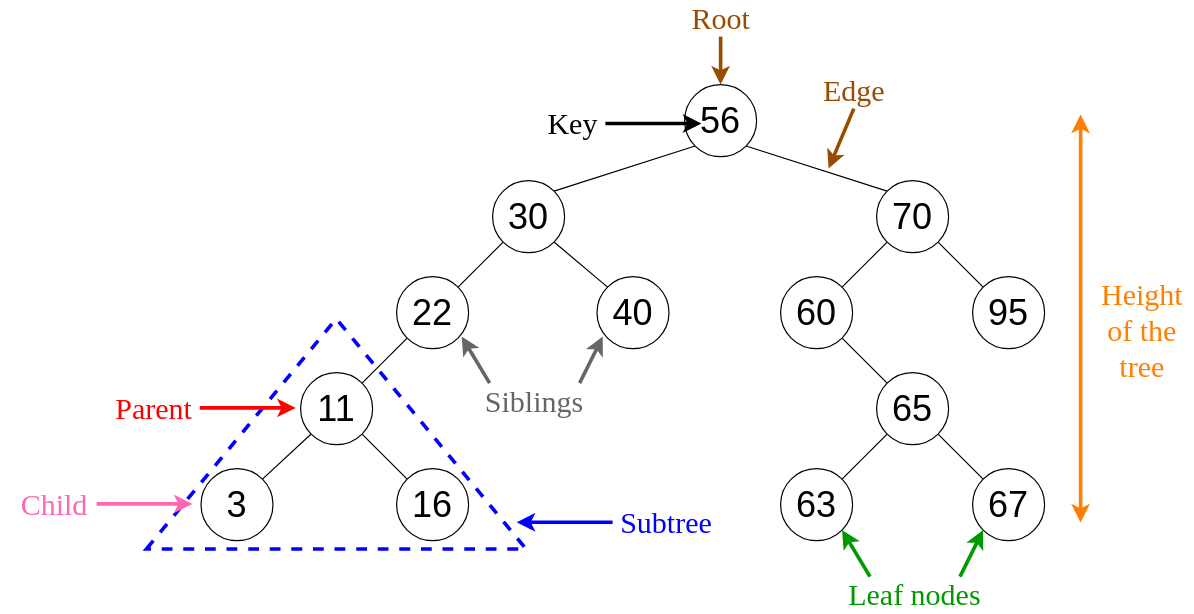
So:
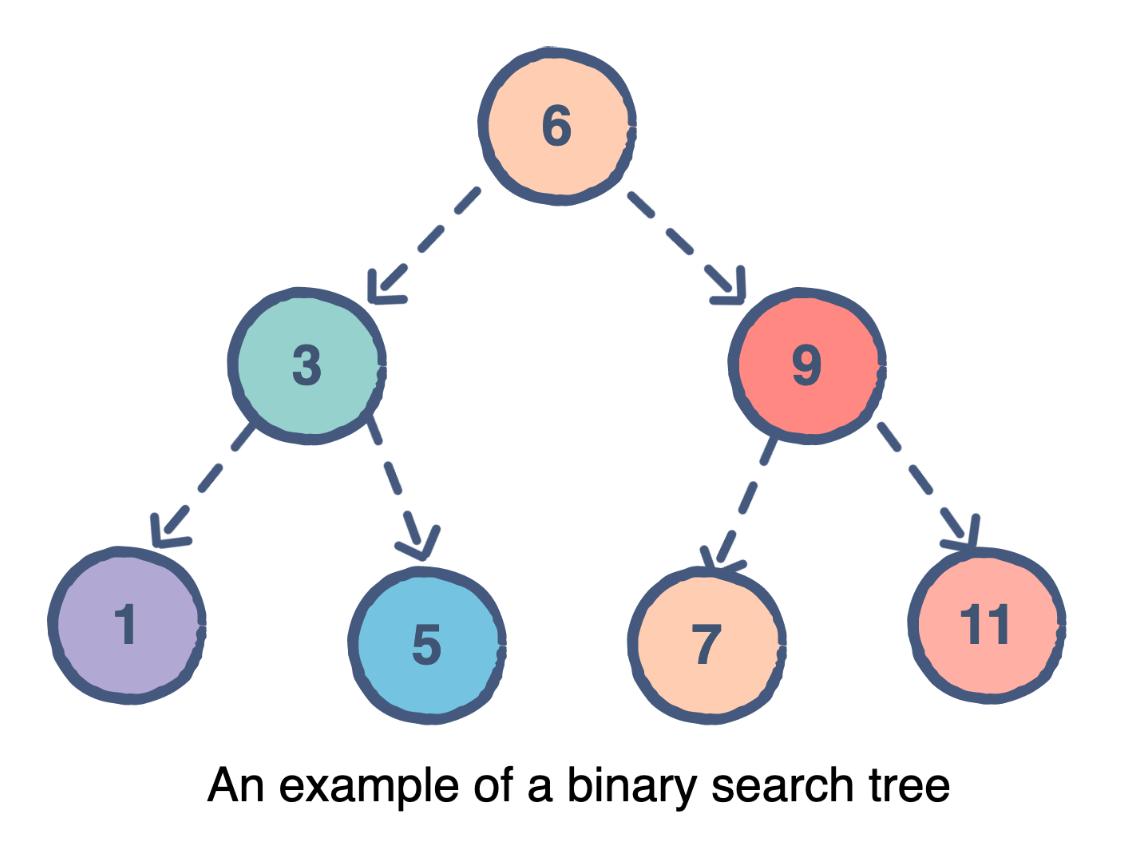
Or this:
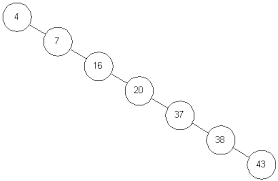
It can be seen that the general binary search tree has different forms, because there are only the following constraints:
- The left subtree is smaller than the root
- The right subtree is larger than the root
Analyze the performance:
- In the optimal case, the binary search tree is a complete binary tree, and its average comparison times is log(N)
- In the worst case, the binary search tree degenerates into a single branch tree, and its average comparison times is N/2
Node insertion
To insert a node, you only need to meet the following requirements after insertion:
- The left subtree is smaller than the root
- The right subtree is larger than the root
The new node will become a new leaf
Here, we agree that the values of each node are different, that is, nodes with duplicate values cannot appear
We need a parent to connect the newly inserted node with the original tree:
bool Insert(K key) {
if (_root == nullptr) {
_root = new Node(key);
}
else {
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
return false;
}
}
cur = new Node(key);
if (key < parent->_key) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
}
return true;
}
Node deletion
Deleting a node is slightly more complicated than inserting it. Please see the following three situations:
1. Delete leaf node
This is simple. Deleting a leaf node has no impact on the parent node. It doesn't need to be adjusted. Just delete it directly
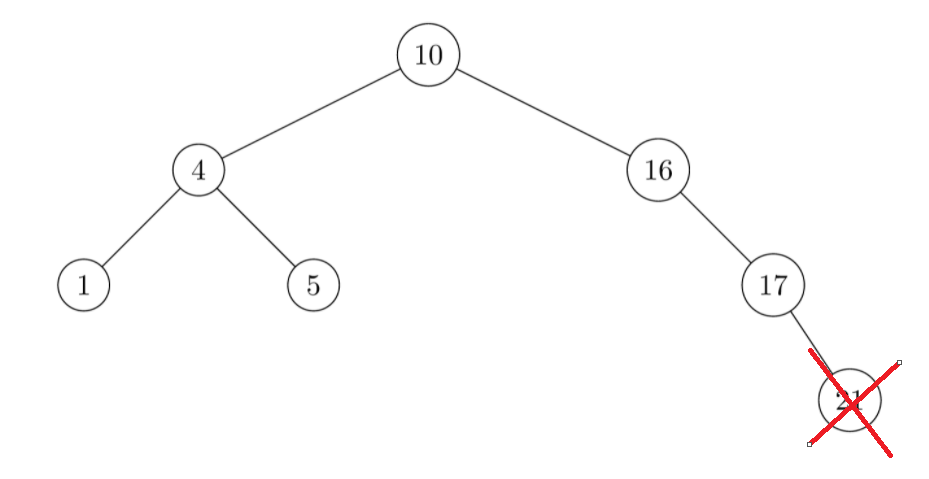
2. The deleted node has only left children or only right children
This is also simple. After deleting a node, just connect the parent node with a single child tree
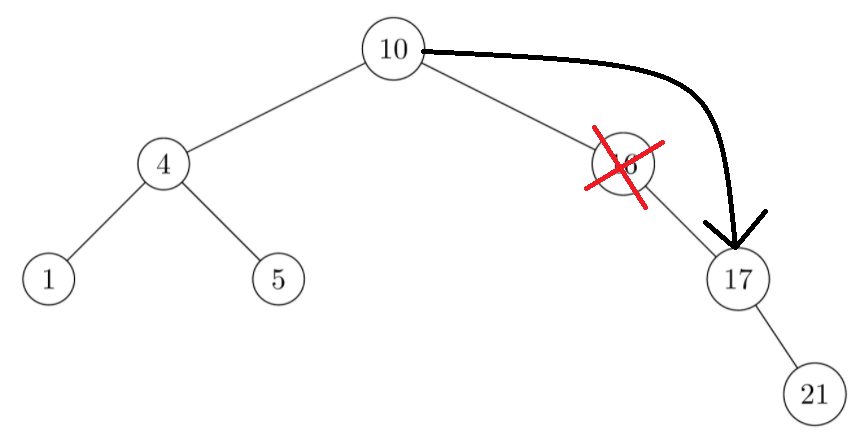
3. Left and right children of the deleted node exist
This is a little difficult. After deleting nodes, you have to adjust the tree
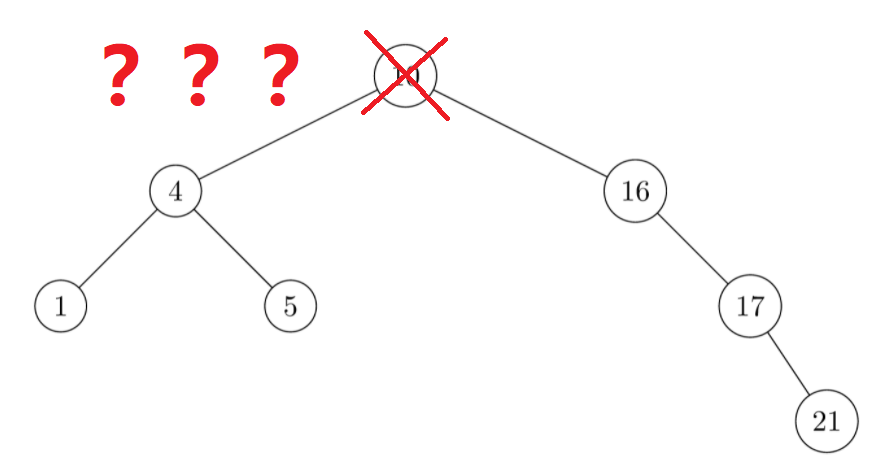
The substitution method can be used to solve:
1. Deleting is to overwrite the value of the original node, so we will directly replace the value of the deleted node with the value of a special node
2. After replacement, the special node will be killed, so when selecting a special node, the better it will be killed and the more suitable it is
3. Who'd better be killed? The first two cases, of course
4. We select a suitable leaf node to replace the position of the deleted node. After replacement, the tree is still a binary search tree
5. Therefore, we can take the point to be deleted as the root and select the largest of its left subtree or the smallest of its right subtree to replace the node to be deleted
Take the smallest right subtree as an example:
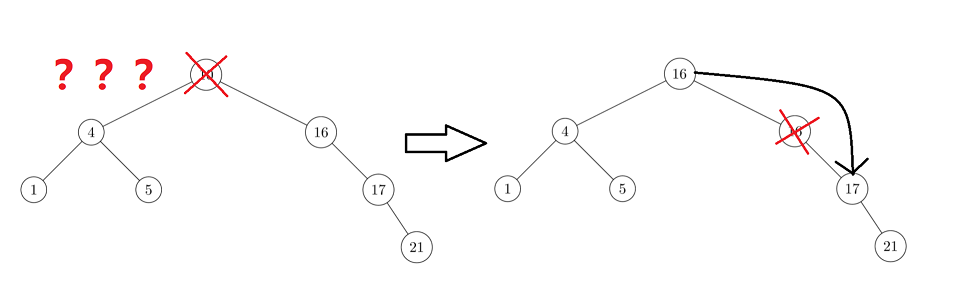
Of course, the right subtree here is a single branch tree, so the smallest is the right child. If it is not a single branch tree, it is the leftmost node of the right subtree
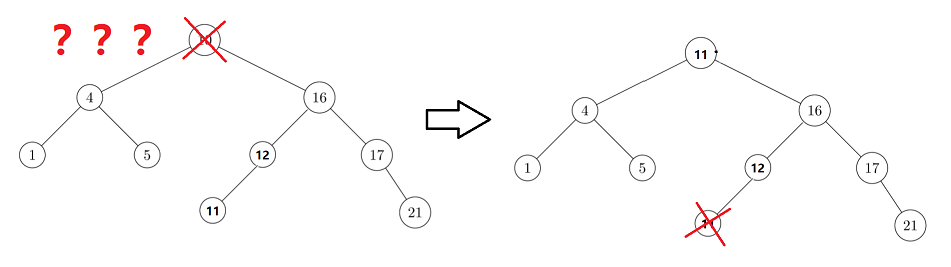
bool Erase(K key) {
// 5
// 3 7
// 1 4 6 8
//0 2 9
// leaf
// Only one child
// There are two children
Node* parent = _root;
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
if (cur->_left == nullptr) {
// Left child is empty
// 1. cur is the root
if (cur == _root) {
_root = cur->_right;
}
// 2. cur is not root
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr) {
// Right child is empty
// 1. cur is the root
if (cur == _root) {
_root = cur->_left;
}
// 2. cur is not root
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else {
// Left and right children are not empty
Node* RLNode = cur->_right;
Node* pRLNode = cur;
Node* ppRLNode = cur;
while (RLNode) {
ppRLNode = pRLNode;
pRLNode = RLNode;
RLNode = RLNode->_left;
}
cur->_key = pRLNode->_key;
if (ppRLNode->_left == pRLNode) {
ppRLNode->_left = pRLNode->_right;
}
else {
ppRLNode->_right = pRLNode->_right;
}
delete pRLNode;
pRLNode = nullptr;
}
return true;
}
}
return false;
}
code
namespace K {
template<class K>
struct BSTreeNode {
K _key;
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
BSTreeNode(K key)
:_key(key)
, _left(nullptr)
, _right(nullptr) {}
~BSTreeNode() {
//delete
//cout << _key << endl;
}
};
template <class K>
class BSTree {
public:
typedef BSTreeNode<K> Node;
BSTree()
:_root(nullptr) {}
bool Insert(K key) {
if (_root == nullptr) {
_root = new Node(key);
}
else {
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
return false;
}
}
cur = new Node(key);
if (key < parent->_key) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
}
return true;
}
Node* Find(K key) {
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
cur = cur->_left;
}
else if (key > cur->_key) {
cur = cur->_right;
}
else {
return cur;
}
}
return nullptr;
}
bool Erase(K key) {
// 5
// 3 7
// 1 4 6 8
//0 2 9
// leaf
// Only one child
// There are two children
Node* parent = _root;
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
if (cur->_left == nullptr) {
// Left child is empty
// 1. cur is the root
if (cur == _root) {
_root = cur->_right;
}
// 2. cur is not root
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr) {
// Right child is empty
// 1. cur is the root
if (cur == _root) {
_root = cur->_left;
}
// 2. cur is not root
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else {
// Left and right children are not empty
Node* RLNode = cur->_right;
Node* pRLNode = cur;
Node* ppRLNode = cur;
while (RLNode) {
ppRLNode = pRLNode;
pRLNode = RLNode;
RLNode = RLNode->_left;
}
cur->_key = pRLNode->_key;
if (ppRLNode->_left == pRLNode) {
ppRLNode->_left = pRLNode->_right;
}
else {
ppRLNode->_right = pRLNode->_right;
}
delete pRLNode;
pRLNode = nullptr;
}
return true;
}
}
return false;
}
void InOrder() {
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root) {
if (root != nullptr) {
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
}
private:
Node* _root;
};
}
namespace KV {
template<class K, class V>
struct BSTreeNode {
K _key;
V _val;
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
BSTreeNode(K key, V val)
:_key(key)
, _val(val)
, _left(nullptr)
, _right(nullptr) {}
~BSTreeNode() {
}
};
template <class K, class V>
class BSTree {
public:
typedef BSTreeNode<K, V> Node;
BSTree()
:_root(nullptr) {}
V& operator[](K key) {
pair<Node*, bool> ret = Insert(key, V());
return ret.first->_val;
}
pair<Node*, bool> Insert(K key, V val) {
if (_root == nullptr) {
_root = new Node(key, val);
return make_pair(_root, true);
}
else {
Node* cur = _root;
Node* parent = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key> cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
return make_pair(cur, false);
}
}
cur = new Node(key, val);
if (key < parent->_key) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
return make_pair(cur, true);
}
}
Node* Find(K key) {
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
cur = cur->_left;
}
else if (key > cur->_key) {
cur = cur->_right;
}
else {
return cur;
}
}
return nullptr;
}
bool Erase(K key) {
// 5
// 3 7
// 1 4 6 8
//0 2 9
// leaf
// Only one child
// There are two children
Node* parent = _root;
Node* cur = _root;
while (cur) {
if (key < cur->_key) {
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key) {
parent = cur;
cur = cur->_right;
}
else {
if (cur->_left == nullptr) {
// Left child is empty
// 1. cur is the root
if (cur == _root) {
_root = cur->_right;
}
// 2. cur is not root
else {
if (parent->_left == cur) {
parent->_left = cur->_right;
}
else {
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr) {
// Right child is empty
// 1. cur is the root
if (cur == _root) {
_root = cur->_left;
}
// 2. cur is not root
else {
if (parent->_left == cur) {
parent->_left = cur->_left;
}
else {
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else {
// Left and right children are not empty
Node* RLNode = cur->_right;
Node* pRLNode = cur;
Node* ppRLNode = cur;
while (RLNode) {
ppRLNode = pRLNode;
pRLNode = RLNode;
RLNode = RLNode->_left;
}
cur->_key = pRLNode->_key;
cur->_val = pRLNode->_val;
if (ppRLNode->_left == pRLNode) {
ppRLNode->_left = pRLNode->_right;
}
else {
ppRLNode->_right = pRLNode->_right;
}
delete pRLNode;
pRLNode = nullptr;
}
return true;
}
}
return false;
}
void InOrder() {
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root) {
if (root != nullptr) {
_InOrder(root->_left);
cout << root->_key << ":" << root->_val << " ";
_InOrder(root->_right);
}
}
private:
Node* _root;
};
}