(I decided to copy my notes from word first.)Perfect as you work on the back)
Tree Array Class 3 Applications
TYPE 1
P1908 Reverse Order Pair
Binary Index Tree
Maintain
Number greater than 6 = total - smaller than him
a:19260817
Discrete
Sort of original array
01126789
Unique weight removal (algorithm)
Arrange Find Above

TYPE 2

Tree arrays maintain x-coordinates

2-D Partial Order
Xi<=xj
Yi<=yj
Because y is given in ascending order, for yj,
3810 3-D Partial Order
Type 3

Fear it's not a tree array board
C How many maintained
Modulate all numbers at the beginning of reading
Then single point plus minus along the strip to take the mode
Consider adding or subtracting the number to or from mod, then adding all the c's that contain it to one

Open m tree arrays, each content is 01
The following table j of the ith tree array
Represents Aj%?=mod

https://www.luogu.org/problemnew/show/P2234
Weight segment tree, an array on weights, not a normal array
Establish segment tree to maintain maximum and minimum values of intervals
Single point modification, interval query

https://www.cnblogs.com/xiaoyezi-wink/p/11105832.html
Segment trees can have multiple lazytag s
CF718C Sasha and Array
https://www.luogu.org/problemnew/show/CF718C
My own Baidu_
Parent Function, Generating Function, Typho-Fibonacci Number General Term Formula
Save feibo directly when saving
Single point modification multiplied by matrix fast power
Convert to an interval to find a number, and sum the intervals
Multiplied by a matrix

https://www.luogu.org/problemnew/show/P4145
The nature of the root sign
Single Modify Opening Root
Modify when it is a leaf node

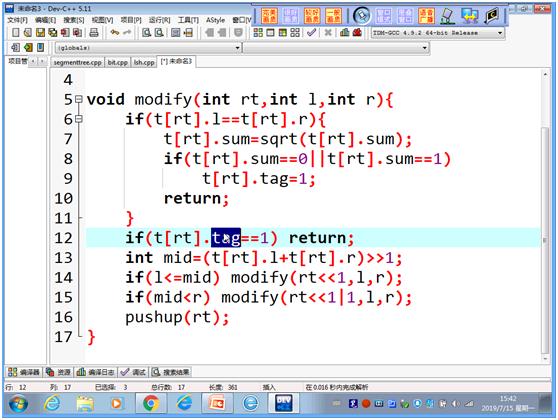
CF85D Sum of Medians
https://www.luogu.org/problemnew/show/CF85D
Array s has only five numbers
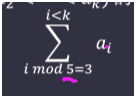
Focus on decimals (long small, not non-integer)
A segment tree is a tree that sorts all the numbers that have been added.
Maintaining an s for each interval indicates how many numbers exist in the interval at the current time
f[0...4], f[k] represents the sum of all AIS for i mod 5 = k
When merging i s s=sl+sr, f[i]=fl[i]+fr[(i-sl)%5]
There's nothing to do below.
Only queries have not been modified

Modify interval to min, mark
The difficulty is to take questions offline

Offline just read in and do whatever you want
Online is read-while-process

P2757 [National Training Team] Isometric Subsequence
https://www.luogu.org/problemnew/show/P2757
Let len=3 directly
Segment Tree Maintenance Hash
- Single point modification
- Compare two intervals
- Each node of the segment tree
All Segment Trees Below NOI
Can't think of working to die

Simplest

NOIP segment tree will not exceed the median difficulty
And Word has a bunch of to-dos
Binary Find Tree
The properties of a binary lookup tree:
For each node, all nodes of its left subtree are smaller than that node, and all nodes of its right subtree are larger than that node
Binary search tree lookup:
From the root node, find elements larger than this point, go to the right of the tree, otherwise go to the left
Pot: Shape is not fixed, find operation depends on depth
Balance Tree: Rotate based on meta-operation
Support interval modification, interval query
Main implementation Splay, Treap
Splay Tree Stretch Tree: Stretch to make the tree less deep
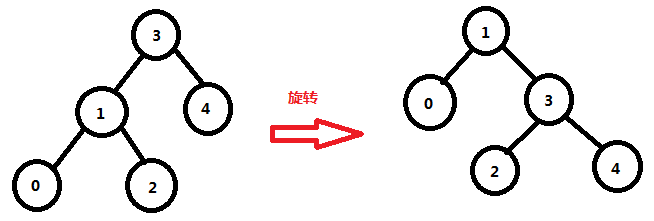
For example, if 1 goes to the root node, one of the sons of 1 runs along and the other to the son of the parent node
If a node has been visited, he is more likely to be visited again later
Splay
Background Profile:
A Splay Tree is a binary search tree that can insert, find, and delete within an O(log n).
It was invented by Daniel Slitter and Robert Enjo Tayan in 1985.
Splay features:
The general operation on an extended tree is based on the stretching operation: suppose you want to perform a series of lookup operations on a binary lookup tree, in order to make the whole lookup time shorter, the entries that are most frequently searched should always be near the root of the tree.Then I thought about designing a simple way to reconstruct the tree after each search and move the items I was looking for closer to the root.Stretching trees emerge as the times require.An extended tree is a self-adjusting form of a binary lookup tree that moves the node to the tree root through a series of rotations along the path from a node to the root.
Splay stretching:
- If at this point, father and grandpa are in a straight line, we turn to father before we turn to ourselves.
- If at this point, father and grandpa twist, we turn ourselves twice in a row.
Why can I turn this tree around???Because for a tree, any node you pick up can be a new shape of the tree.
The most important thing about splay is its adaptive thinking
It also maintains the average allocation time complexity without any restrictions on tree height (relative to treap control expected tree height, RBT/AVL/WBT control tree height)
splay is
First you need to rotate
Then you need to know to twist a point to the root
Then you just need to screw up the found point at the end of any operation
P3369 [Template] General Balanced Tree
https://www.luogu.org/problemnew/show/P3369
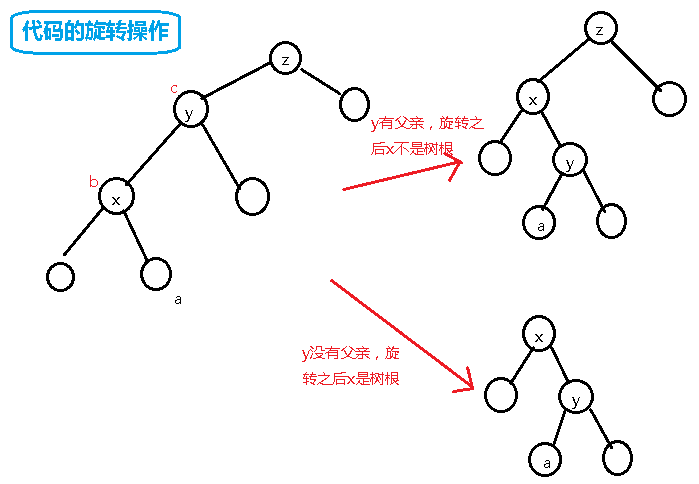
int fa[N],ch[N][2]; //ch[n] 0 They are left sons and right sons. int cnt[N]; //Record n Number of occurrences int data[N]; //Record n Weight value int siz[N]; //Current Node n And its subtrees int son(int x) //see x Is it father's left son 0 or right son 1 { return x==ch[fa[x]][1]; } void pushup(int rt) //Statistics, Upload siz { siz[rt]=siz[ch[rt][0]]+siz[ch[rt][1]]+cnt[rt]; } void rotate(int x) //Rotate operation, after which the properties of a binary lookup tree still need to be satisfied { int y=fa[x],z=fa[y]; int b=son(x),c=son(y); //Record x,y Which side of the father is it? int a=ch[x][!b]; //x The reverse son of the position if(z) ch[z][c]=x,fa[x]=z; //If z existence ,x Father becomes z else root=x; //z Does not exist, then after rotation x It's the root if(a) fa[a]=y; ch[y][b]=a; //Handle x,z Relationships ,Look at the picture ch[x][!b]=y;fa[y]=x; //y Relative to x Of a Location //Handle x,y Relationship, see picture pushup(y);pushup(x); //Upload node information } //Two sons, one following, the other following void splay(int x,int i)//x Transfer to i On his son { while(fa[x]!=i) //x No i Son, has been turning { int y=fa[x],z=fa[y]; if(z==i) //If i yes x Grandpa, direct rotation { rotate(x); } else { if(son(x)==son(y)) //If the current point, father, grandpa, turn father to himself { rotate(y);rotate(x); } else //If at this point, father and grandpa twist, they turn themselves twice in a row { rotate(x);rotate(x); } } } } void insert(int &rt,int x){ //Insert operation if(rt==0) //This node never appears, create a new point { rt=++nn; //nn Is the total number of nodes, rt Is the node number data[rt]=x; //assignment siz[rt]=cnt[rt]=1; return; } if(x==data[rt])//If x It's equal to the current node, it's been there before,+1 Just fine { cnt[rt]++; //Number of this number+1 siz[rt]++; //Number of subtree nodes+1 return; } if(x<data[rt])//x Smaller than current node { insert(ch[rt][0],x); //Insert into left subtree fa[ch[rt][0]]=rt; //Marking the left son's father as himself pushup(rt); //upload siz } else//x Greater than current node { insert(ch[rt][1],x); //Insert Right Subtree fa[ch[rt][1]]=rt; //Mark the right son's father as himself pushup(rt); //upload siz } } //Find a Front End //Precursor, less than x Maximum int getpre(int rt,int x) { int p=rt,ans; //p Is the number of the current node, ans yes x A pioneer while(p) { if(x<=data[p]) //x Smaller than current node, go left subtree { p=ch[p][0]; } else //Otherwise, go to the right subtree and keep moving closer to the optimal pioneer { ans=p; p=ch[p][1]; } } return ans; } //Subsequent, greater than x Minimum value int getsuc(int rt,int x) { int p=rt,ans; while(p) { if(x>=data[p]) { p=ch[p][1]; } else { ans=p; p=ch[p][0]; } } return ans; } //Find rt Continue to walk left subtree for minimum value of root tree int getmn(int rt) { int p=rt,ans=-1; while(p) { ans=p; p=ch[p][0]; } return ans; } //Delete weights are x Node void del(int rt,int x) { if(data[rt]==x) //Found this node, ready to delete { if(cnt[rt]>1)//Node is not one, then delete only one { cnt[rt]--; siz[rt]--; } else //There is only one node { splay(rt,0); //Rotate the point to be deleted to the root node (root node number is 0) int p=getmn(ch[rt][1]); //Find greater than rt Minimum Right Son if(p==-1) //Not found, then rt And his right son is greater than rt Minimum value { root=ch[rt][0]; //Use ratio rt Large minimum instead rt ,delete rt fa[ch[rt][0]]=0; //Mark Root Node } else //greater than rt The minimum value exists rt In the left subtree of the right son { splay(p,rt); //hold p go to rt Location root=p;fa[p]=0; //Minimum as New Root ch[p][0]=ch[rt][0]; //rt The left son of p Below fa[ch[rt][0]]=p; //Mark Father pushup(p); //upload siz } } return; } if(x<data[rt]) //Go to the left subtree to find { del(ch[rt][0],x); } else { del(ch[rt][1],x); } pushup(rt); //pushup statistical information } int getk(int rt,int k) //Weighting k Node ranking { if(data[rt]==k) //The current node is k { splay(rt,0); //Move the current node to the root if(ch[rt][0]==0) //If it has no left subtree, then it rank 1 { return 1; } else //Otherwise its rank Is the number of all nodes in the left subtree+1 { return siz[ch[rt][0]]+1; } } if(k<data[rt]) return getk(ch[rt][0],k); if(data[rt]<k) return getk(ch[rt][1],k); } int getkth(int rt,int k) //Find ranking k Node { int l=ch[rt][0]; //Find the left son of the current node if(siz[l]+1<=k&&k<=siz[l]+cnt[rt]) return data[rt]; //If k More than left subtree nodes but plus rt And then less than it, then rt Is number one k Node if(k<siz[l]+1) return getkth(l,k); //Go to the left subtree else return getkth(ch[rt][1],k-siz[l]-cnt[rt]); //Go to the subtree on the right }