Data structure - tree structure
First of all, what is a tree structure? In short, the tree structure is the structure you think now. The data structure like a tree is a tree structure. Typical tree structure examples: Windows operating system, Unix operating system and file system are all applications of tree structure.
-
Basic concepts of tree
**A Tree * * is composed of one or more nodes. There is a special Node called root. Root is familiar with Linux root directory. Each Node is a record composed of some data and pointers
A B C D A is the root node, and B, C and D are the child nodes of A
Trees can also form forests, that is, forests are a collection of N mutually exclusive trees (n > = 0), and moving tree roots are forests
Simply put, removing the root node is the forest, which is outrageous enough
Proper noun of tree structure
In the tree structure, there are many commonly used proper nouns
- Degree: the number of all words in each node. For example, the degree of A is 3
- Level: the number of layers of the tree. For example, A is in the first layer and B, C and D are in the second layer
- Height: the maximum number of layers of a tree. For example, the height above is 2
- Leaves or terminal nodes: nodes with zero degrees are leaves, and nodes B, C and D are leaves
- Parent node: each node has a connected upper node
- Children: each node is connected, and the next node is a child node
- Ancestor and descendant: the so-called ancestor refers to the node contained in the path from the tree root to the node, and the descendant refers to any node in the subtree traced down from the node. (these things are the same as your biological genealogy. Just look at the analogy)
- Siblings: a node with a common parent node is a sibling node
- Non terminal nodes: nodes other than leaves
- Generation: nodes with the same number of layers in the same tree
-
Introduction to binary tree
Generally, the storage mode of tree structure in computer memory is mainly linked list. For n-way trees, because the degrees of each node are different, we must reserve the maximum storage space for n link fields for each node, because the data structure of each node is as follows:
data link1 link2 link3 ... ... linkn In this case, this n-ary tree is a waste of link storage space. Assuming that the n-ary tree has m nodes, the tree has nxm link fields. In addition, because each non empty link points to a node except the tree root, it is known that the number of empty links is nxm-(m-1) = m x (n-1) + 1, and the link waste rate of n-ary tree is [m x (n - 1) + 1]/m x n. therefore, the following conclusions can be drawn:
When n = 2, the link waste rate of binary tree is about 1 / 2
When n = 3, the link waste rate of 3-ary tree is about 1 / 3
When n = 4, the link waste rate of 4-ary tree is about 1 / 4
... ...
... ...
When n = 2, its link waste rate is the lowest. Therefore, in order to improve the waste of storage space, binary tree structure is most often used to replace other tree structures
-
Definition of binary tree
Binary tree (also known as Knuth tree) is a set composed of finite nodes. This set can be an empty set or composed of a number root and its left and right subtrees. In short, a binary tree can only have two child nodes at most, that is, the degree is less than or equal to 2 The data structure in the phase I computer is as follows:
LLINK Data ALINK Differences between binary tree and general tree:
- A tree cannot be an empty set, but a binary tree can
- The degree of the tree is d > = 0, but the node degree of the binary tree is 0 < = d < = 2
- There is no order relationship between the subtrees of a tree, while a binary tree has
-
Special binary tree
-
Full binary tree
If the height of the binary tree is h, the number of nodes of the tree is 2^h - 1, and H > = 0, we call the tree "full binary tree"
-
Complete binary tree
If the height of the binary tree is h, the number of nodes is less than 2^h - 1, but the numbering method of its nodes is the same as that of the full binary tree with height h, which corresponds one by one from left to right and from top to bottom
For a complete binary tree, if there are N nodes, the number of layers h of the binary tree is * * [log2(N+1)]**
-
Skew binary tree: when a binary tree has no nodes or left nodes at all, we call it left skew binary tree or right skew binary tree
-
Strict binary tree
Each non terminal node in the binary tree has a non empty left and right subtree
-
-
Storage method of binary tree
Binary tree has many storage methods. In data structure, we usually use linked list to represent binary tree, which will be very convenient and convenient when deleting or adding nodes. However, a continuous storage space such as a one-dimensional array can also be used to represent a binary tree. However, when inserting or deleting intermediate nodes in the tree, it may be necessary to move a large number of storage locations of nodes in the array to reflect the changes of tree nodes
-
One dimensional array representation
An ordered one-dimensional array is used to represent the binary tree. Firstly, the binary tree can be assumed to be a full binary tree, and the K-th layer has 2^k-1 nodes, which are stored in this one-dimensional array in order.
(1) A (root node) (1)B (3) None (4) None (5)C (6) None (7)D What is it like to store the above binary tree into a one-dimensional array
Index value 1 2 3 4 5 6 7 Content value A B C D It can be seen from the direct relationship between the index value of binary tree and one bit array
- The index value of the left subtree is the index value of the parent node * 2
- The index value of the right subtree is the index value of the parent node * 2 + 1
Next, let's look at the example of establishing a binary tree with a one-dimensional array. In fact, it is to create a binary search tree, which is a good sorting application model, because while establishing a binary tree, the data will undergo preliminary comparison and judgment and store the data according to the establishment rules of the binary tree. Binary search tree has the following characteristics:
- It can be an empty set, but if it is not an empty set, there must be a key value on the node
- The value of each tree root needs to be greater than the value of the left subtree
- The value of each tree root should be less than the value of the right subtree
- The left and right subtrees are also binary search trees
- Each node of the tree has different values
Example: design a program to input a binary tree as needed
Note that because the size of the array is fixed, it is easy to exceed the index limit in data design, so find a data support to match it
def Btree_create(btree,data,length): for i in range(1,length): level = 1 while btree[level] != 0: if data[i] > btree[level]: #Judge the comparison between the data in the data and the tree root, and put it on the right level = level * 2 + 1 #Assign level to the next node. If there is data, cycle through the next node else: level = level * 2 #Less than is placed on the left, * 2, and the level is assigned to the next node. If there is a data loop, traverse the next node btree[level] = data[i] #Traverse to get the level without value and assign it a value data = [0,3,5,6,1,9,3,2,1] length = 9 btree = [0] * 16 print("Original array contents") for i in range(length): print('[%2d]'% data[i],end='') print('') Btree_create(btree,data,9) print('Binary tree content') for i in range(1,16): print('[%2d]'%btree[i],end='') print('')
-
Linked list representation
Linked list representation is to use linked list to store binary tree. The advantage of using linked list to represent binary tree is that it is quite easy to add and delete nodes. The disadvantage is that it is difficult to find the parent node, unless one more parent field is added to each node. Take the data type storing integers as an example
class tree: def __init__(self): self.data = 0 self.left = None self.right = None
Establish binary tree by linked list
def create_tree(self,root,val): newnode = tree() #Instantiate a node newnode.data = val #Assign data newnode.left = None #The left node points to None newnode.right = None #The right node points to None if root == None: root = newnode #If there is no parent node, assign newnode to root return root else: current = root while current != None: backup = current #Give the current value of each traversal to backup if current.data > val: #If the value of the node is greater than val, put val on the left and set current as the next node on the left current = current.left #current is the next node on the left else: #If the value of the node is less than val, put val on the right and set current as the next node on the right current = current.right #current is the next node on the right if backup.data > val: #Compare the backup (current) and val at this time to determine which side of the backup the newnode is placed on backup.left = newnode else: backup.right = newnode return rootTo summarize the above code, the while loop is to traverse the node current until the new node is placed when the next node is found to be empty. The first if is to determine whether to traverse left or right when the current node is not empty, and the second if is to determine whether the new node should be placed to the left or right when the node is empty
Design program, use linked list to establish binary tree
class tree: def __init__(self): self.data = 0 self.left = None self.right = None def create_tree(root,val): newnode = tree() #Instantiate a node newnode.data = val #Assign data newnode.left = None #The left node points to None newnode.right = None #The right node points to None if root == None: root = newnode #If there is no parent node, assign newnode to root return root else: current = root while current != None: backup = current #Give the current value of each traversal to backup if current.data > val: #If the value of the node is greater than val, put val on the left and set current as the next node on the left current = current.left #current is the next node on the left else: #If the value of the node is less than val, put val on the right and set current as the next node on the right current = current.right #current is the next node on the right if backup.data > val: #Compare the backup (current) and val at this time to determine which side of the backup the newnode is placed on backup.left = newnode else: backup.right = newnode return root data = [5,4,8,1,12,3,6,7,9] ptr = None root = None for i in range(9): ptr = create_tree(ptr,data[i]) print('Left subtree') root = ptr.left while root != None: print('%d' %root.data) root = root.left print('--------------') print('Right subtree') root = ptr.right while root != None: print('%d'%root.data) root = root.right print()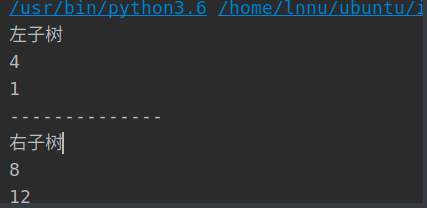
-
-
Traversal of binary tree
Linear arrays or linked lists can only be traversed one way from beginning to end or reverse. The so-called traversal of binary tree is simply to visit all nodes in the tree once, and after traversal, convert the data in the tree into linear relationship. Binary tree can divide each node into left and right branches
The characteristics of binary trees are traversed from left to right, so there are three traversal methods, namely
- Middle order traversal: left subtree - > tree root - > right subtree
- Pre order traversal: tree root - > left subtree - > right subtree
- Post order traversal: left subtree - > right subtree - > tree root
The order of these three methods is also very easy to remember. In short, "from left to right, the tree root is the best", which means that all traversal sequences are from left to right. Where the tree root is, it belongs to what traversal. The tree root in front is the pre order traversal, the tree root in the middle is the middle order traversal, and the tree root behind is the post order traversal
The following describes the algorithm implementation of traversal in three ways
-
Middle order traversal
The middle order traversal order is: left subtree - > tree root - > right subtree
It is to move down from the left side of the tree step by step until it cannot be moved, then access this node and move a node to the right. If you cannot move to the right, you can return to the upper parent node and repeat this step
- Traverse left subtree
- Traversing tree roots
- Traversing right subtree
In this way, the recursive method can be used. Recursively find the leftmost node, then the right, and finally the tree root. The exit is when the node is empty
""" Middle order traversal """ def inorder(ptr): if ptr != None: inorder(ptr.left) print('[%2d]' % ptr.data,end='') inorder(ptr.right) -
Postorder traversal
The order of traversal is: left subtree - > right subtree - > tree root
That is, first traverse the left subtree, then traverse the right subtree, and finally traverse the root node. Repeat this step repeatedly
- Traverse left subtree
- Traversing right subtree
- Traverse tree root
""" Postorder traversal """ def postorder(ptr): if ptr != None: postorder(ptr.left) postorder(ptr.right) print('[%2d]' % ptr.data,end='') -
Preorder traversal
The order of traversal in the preceding order is: tree root - > left subtree - > right subtree
First traverse from the root node, and then move to the left. When it cannot be moved, continue to move to the right, and then repeat this step
- Traversing tree roots
- Traverse left node
- Traverse right node
""" Preorder traversal """ def preorder(ptr): if ptr != None: print('[%2d]' % ptr.data,end='') preorder(ptr.left) preorder(ptr.right)To sum up:
The functions required for the algorithm implementation of the three traversal methods are similar, but the steps are sequential. They all traverse the left subtree and the right subtree. The difference is to see which step to deal with
The details of the running process of this recursive algorithm take the middle order as an example:
""" Middle order traversal """ def inorder(ptr): """ Judge whether this node is empty. If it is not empty, enter. If the first node is empty, it indicates that the binary tree is empty """ if ptr != None: """ Call this function for the next left node. If it is empty, it means it is the leftmost side of the subtree. If it is not empty, continue to call the next left node until the leftmost side is found """ inorder(ptr.left) """ After executing the above code, find the leftmost node and output the node """ print('[%2d]' % ptr.data,end='') """ Find the next right node. Note that after this step, the left and middle nodes have been output, so find the right node """ inorder(ptr.right)Because the rule of binary tree is: left subtree < root node < right subtree
Therefore, if you use medium order traversal, you will find that the output results have been sorted from small to large
Example: design program, middle order, post order and pre order traverse binary tree
-
class tree:
def __init__(self):
self.data = 0
self.left = None
self.right = None
"""
Middle order traversal
"""
def inorder(ptr):
if ptr != None:
inorder(ptr.left)
print('[%2d]' % ptr.data,end='')
inorder(ptr.right)
"""
Postorder traversal
"""
def postorder(ptr):
if ptr != None:
postorder(ptr.left)
postorder(ptr.right)
print('[%2d]' % ptr.data,end='')
"""
Preorder traversal
"""
def preorder(ptr):
if ptr != None:
print('[%2d]' % ptr.data,end='')
preorder(ptr.left)
preorder(ptr.right)
"""
Establish binary tree
"""
def create_tree(root,val):
newnode = tree()
newnode.data = val
newnode.left = None
newnode.right = None
if root == None:
root = newnode
return root
else:
current = root
while current != None:
backup = current
if current.data > val:
current = current.left
else:
current = current.right
if backup.data > val:
backup.left = newnode
else:
backup.right = newnode
return root
"""
main program
"""
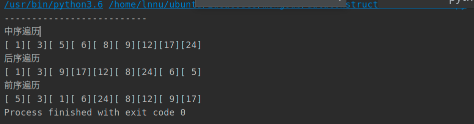
data = [5,6,24,8,12,3,17,1,9]
ptr = None
root = None
for i in range(9):
ptr = create_tree(ptr,data[i])
print("--------------------------")
print("Middle order traversal")
inorder(ptr)
print('')
print('Postorder traversal')
postorder(ptr)
print('')
print('Preorder traversal')
preorder(ptr)
- Insertion and deletion of binary tree nodes
Discuss how to find the data in a binary tree before inserting it into a single node. Start from the tree root and compare the key values. If it is larger than the tree root, go to the right, otherwise go to the left until the value to be searched is found. If it is found, go to the left None If it cannot be checked, it means that there is no such value
```python
"""Find node"""def searchnode(ptr,val): i = 1 while True: if ptr == None: return None if ptr.data == val: print('Total found%3d second' %i) return ptr elif ptr.data > val: ptr = ptr.left else: ptr = ptr.right i += 1 print(ptr.data)
```
-
Example: implement a binary tree search program
class tree: def __init__(self): self.data = 0 self.left = None self.right = None """ Find node """ def searchnode(ptr,val): i = 1 while True: if ptr == None: return None if ptr.data == val: print('Total found%3d second' %i) return ptr elif ptr.data > val: ptr = ptr.left else: ptr = ptr.right i += 1 print(ptr.data) """ Establish binary tree """ def create_tree(root,val): newnode = tree() newnode.data = val newnode.left = None newnode.right = None if root == None: root = newnode return root else: current = root while current != None: backup = current if current.data > val: current = current.left else: current = current.right if backup.data > val: backup.left = newnode else: backup.right = newnode return root """ main program """ data = [5,6,24,8,12,3,17,1,9] ptr = None print('[Original array contents]') for i in range(9): ptr = create_tree(ptr,data[i]) print('[%2d]' % data[i],end='') print() node = int(input("Please enter a lookup value:")) if searchnode(ptr,node) != None: print('The value you found[%3d]eureka!!' % node) else: print('The value you are looking for is not found!!')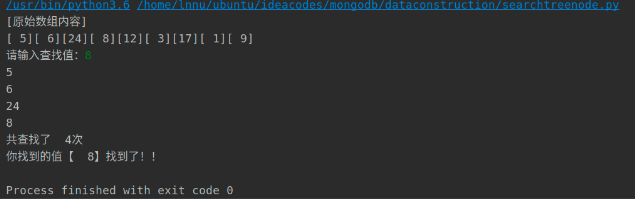
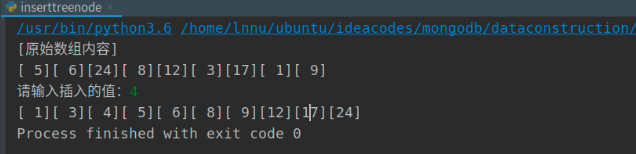
- Insertion of binary tree nodes The insertion of binary tree nodes is similar to search. The key point is to maintain the characteristics of binary search tree after insertion. If the inserted node is already in the binary tree, there is no need to insert it. If the inserted value is not in the binary tree, the search will fail, which is equivalent to finding the location to be inserted ```python if serch(ptr,data) != None: print('There is this node in the binary tree!')else: ptr = create_tree(ptr,data) inorder(ptr) ``` Implement a program to add binary tree nodes and traverse in sequence ```python class tree: def __init__(self): self.data = 0 self.left = None self.right = None """ Find node """ def searchnode(ptr,val): i = 1 while True: if ptr == None: return None if ptr.data == val: return ptr elif ptr.data > val: ptr = ptr.left else: ptr = ptr.right i += 1 """ Establish binary tree """ def create_tree(root,val): newnode = tree() newnode.data = val newnode.left = None newnode.right = None if root == None: root = newnode return root else: current = root while current != None: backup = current if current.data > val: current = current.left else: current = current.right if backup.data > val: backup.left = newnode else: backup.right = newnode return root """ Middle order traversal """ def inorder(ptr): if ptr != None: inorder(ptr.left) print('[%2d]' % ptr.data,end='') inorder(ptr.right) """ main program """ data = [5,6,24,8,12,3,17,1,9] ptr = None print('[Original array contents]') for i in range(9): ptr = create_tree(ptr,data[i]) print('[%2d]' % data[i],end='') print() node = int(input("Please enter the inserted value:")) if searchnode(ptr,node) != None: print('The node value already exists in the binary tree') else: ptr = create_tree(ptr,node) inorder(ptr) ```
- **Deletion of binary tree nodes**
The deletion of binary tree nodes can be divided into three cases:
- The deleted node is a leaf, as long as its connected parent node points to None that will do
- The deleted node has only one subtree. After deletion, the subtree should be placed in its own position and connected to its parent node
- The deleted node has two subtrees. There are two deletion methods. Although the results are not used, they all conform to the characteristics of binary tree
- Find out the immediate first mover in the middle order, that is, raise the largest one in the left subtree of the node to be deleted
- Find the immediate successor in the middle order, that is, raise the smallest one in the right subtree of the node to be deleted
- **Binary operation tree**
We can build the middle order expression into a binary operand in the order of operator priority. Then, according to the characteristics of binary tree, traverse the front, middle and rear order to get the expression of front, middle and rear order method. The method can be established according to the following two rules:
- Considering the associativity and priority of operators in the expression, and properly adding parentheses, the number must also be the operand, and the internal node must be the operator
- Then step outward from the innermost bracket, using the operation as the tree root, the left operand as the left subtree, and the right operand as the right subtree, in which the operator with the lowest priority is the tree root of the binary operation tree
-
Clue binary tree
The storage rate of a pointer can be reduced from 1 / 2 of a binary tree to 2 / 3 of a binary tree However, for a binary tree with n nodes, in fact, only n-1 links are used to point to the left and right nodes, and the other n+1 pointers are empty links
The so-called clue binary tree is to make use of these empty links and then point to other nodes of the tree. These links are called clues and the tree is called binary tree. The biggest advantage is that when traversing the middle order, you don't need to use recursion and stack. You can directly use the pointers of each node
-
Binary tree to clue binary tree
The biggest difference between the online binary tree and the binary tree: in order to distinguish whether the left and right subtree pointers are clues or normal link pointers, we must add two fields LBIT and RBIT in the node structure to distinguish them. In the drawing, the clues are represented by dotted lines, so as to be different from general pointers. The binary tree is transformed into a clue binary tree:
- First, the binary tree is arranged in order according to the middle order traversal mode, and then all empty links are changed into clues
- If the clue link is a left pointer to the node, the clue is pointed to the previous node in the middle order traversal order
- If the right pointer to the node is pointed to when the clue is linked, the clue will be pointed to the next node in the middle order traversal order
- Point to an empty node and point the right pointer of this node to itself, and the left subtree of the empty node is the clue binary tree
The basic structure of clue binary tree is as follows:
LBIT LCHILD DATA RCHILD RBIT - LBIT: left control bit
- LCHILD: left subtree link
- DATA: node DATA
- RCHILD: right subtree link
- RBIT: right control bit
The difference between the binary tree and the linked list is that in order to distinguish between normal pointers and clues, two fields are added: LBIT and RBIT
- If LCHILD is a normal pointer, LBIT=1
- If LCHILD is a clue, LBIT=0
- If RCHILD is a normal pointer, RBIT=1
- If RCHILD is a clue, RBIT=0
class Node: def __init__(self): self.DATA=0 self.LBIT=0 self.RBIT=0 self.LCHILD=None self.RCHILD=None
Advantages and disadvantages of using clue binary tree:
advantage:
- Stack processing is not required when traversing a binary tree, but it is required for a general binary tree
- Due to the full use of empty links, the idle waste of links is avoided. In addition, the middle order traversal speed is also faster, saving a lot of time
- It is easy for any node to find its middle order forerunner and middle order successor. There is no need to use stack or recursion during middle order traversal
Disadvantages:
- The speed of adding or deleting nodes is slower than that of general binary trees
- Cables cannot be shared between sub trees
-
-
Binary tree representation of tree
-
Convert tree to binary tree
The method used to convert a general tree structure into a binary tree is called CHILD-SIBLING rule. The following steps are performed:
- Connect all the sibling nodes of the node with horizontal lines
- Delete all links with child nodes, and only keep the links with the leftmost child nodes
- Rotate 45 degrees clockwise
-
Binary tree to tree
Since the tree can be transformed into a binary tree, the reverse can certainly be achieved. The transformation of a binary tree into a tree is the reverse process of the transformation of a tree into a binary tree. First, rotate it 45 degrees counterclockwise, increase the connection according to the parent-child relationship, and delete the connection between brother nodes
-
Convert forest to binary tree
In addition to a tree can be converted into a binary tree, the forest formed by several trees can also be converted into a binary tree
- Connect the roots of each tree from left to right
- The method of transforming a tree into a binary tree is still used
-
Binary tree into forest
The method of converting a binary tree into a forest is to go back according to the method of converting a forest into a binary tree, that is, rotate the original tree 45 degrees counterclockwise, and then divide it step by step according to the principle that the left subtree is a parent-child relationship and the right subtree is a brother relationship
-
Traversal of trees and forests
In addition to the traversal of binary tree, there are three methods: middle order traversal, pre order traversal and post order traversal, so are the traversal of tree and forest
Assuming that the root of the tree is R, the tree has n nodes and can be divided into m subtrees, T1, T2,..., Tm respectively
Then the steps of traversing the method are as follows:
- Middle order traversal
- Traverse T1 in middle order
- Access tree root R
- Then traverse T2, T3,..., Tm with the middle order method
- Preorder traversal
- Access tree root R
- Then the previous order method traverses T1, T2, T3,..., Tm in turn
- Postorder traversal
- The subsequent sequence method accesses T1,T2,T3,..., Tm in turn
- Access tree root R
Forest traversal is derived from tree traversal
- Middle order traversal
- If the forest is empty, return directly
- Traverse the subtree group of the first tree in medium order
- Traverse the roots of the first tree in the forest in middle order
- Traverse other trees in the forest according to the middle order method
- Preorder traversal
- If the forest is empty, return directly
- Traverse the roots of the first tree in the forest
- Traverse the subtree group of the first tree in the previous order
- Traverse other trees in the forest according to the previous order method
- Postorder traversal
- If the forest is empty, return directly
- Traverse the subtree of the first tree in the following order
- Traverse other trees in the forest according to the post order method
- Facilitate the root of the first tree in the forest
- Middle order traversal
-
Determine unique binary tree
Among the three traversal methods of binary tree, if there are traversal results of middle order and pre order or middle order and post order, the unique binary tree can be obtained from these results. However, if there are only pre order and post order traversal results, the unique binary tree cannot be determined
-
Optimize binary lookup tree
-
extended binary tree
In any binary tree, if there are n nodes, there are n-1 non empty links and n+1 empty links. If a specific node is added to each empty link, it is called an outer node, and the other nodes are called inner nodes. Therefore, this kind of tree is defined as an extended binary tree. Another definition: outer diameter length = the sum of the distances from all outer nodes to the tree root, and inner diameter length = the sum of the distances from all inner nodes to the tree root
-
huffman tree
Huffman tree is often used to deal with data compression. It can build a binary tree according to the frequency of data.
In short, if there are n weights and a binary tree with n nodes is formed, and the weight of the external node of each node is qi, the one with the smallest weighted outer diameter length is called optimized binary tree or "Huffman tree"
-
Balanced tree
In order to minimize the search time, find the required key value quickly, or know that there is no key value in the current tree, the smaller the height of the tree, the better
Because the disadvantage of binary search tree is that it can not be kept in the best state forever. When the data part has been sorted, it is very likely to produce oblique binary tree, because the height of the tree increases, resulting in the reduction of search efficiency. Therefore, the general binary search tree is not suitable for the situation of frequent data changes
definition
The so-called balanced tree, also known as AVL tree (invented by Adelson velskii and Landis), is also a binary search tree. In AVL tree, after inserting and deleting data every time, some height adjustments will be made to the binary tree when necessary, and these adjustments are to keep the height of the binary search tree balanced at any time
-
-