Tree 2021 / 8 / 8 20:00

Except for the root node, any node has and has only one precursor

Common properties of trees

Property 1: number of nodes = total degree + 1 (there is an antenna on the head of any node except the root node)
Property 2: tree with degree m: the maximum degree of each node in the tree
m-ary tree: a tree with at most m children per node
Pay attention to the difference between the two!!!!
Property 3: the M-ary tree with height h has at most (m^h-1) / (m-1) nodes
Property 4: the M-ary tree with height h has at least h nodes, and the tree with height h and degree m has at least h+m-1 nodes
Nature 5:

Binary tree

Full binary tree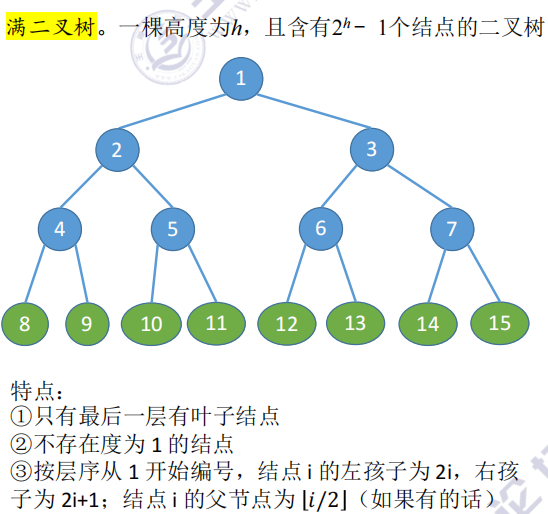

Complete binary tree

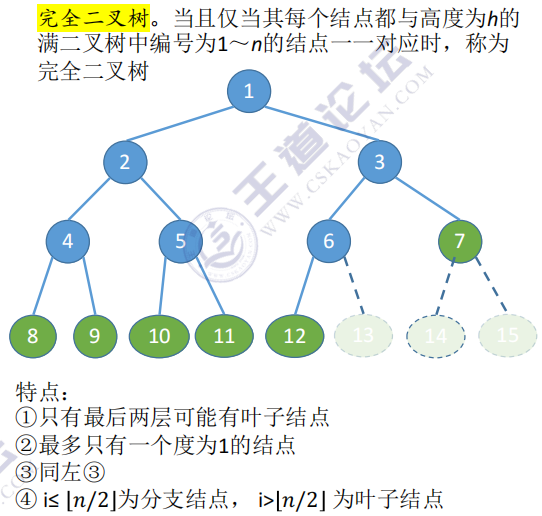
If a node of a complete binary tree has only one child, it must be the left child

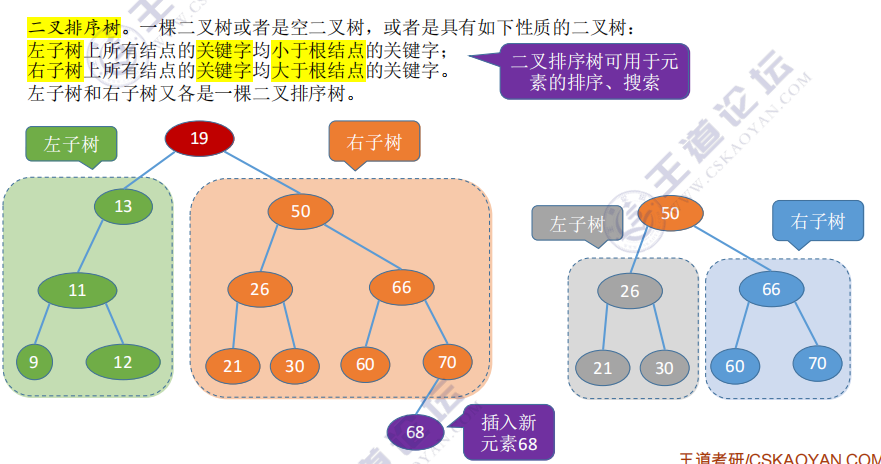
Binary sort tree

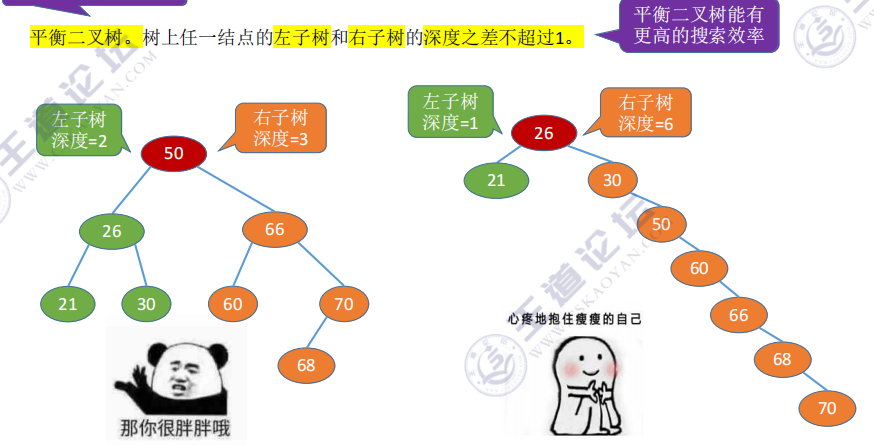
balanced binary tree

Common properties of binary trees

Property 1: let the number of nodes with moderate 0, 1 and 2 of non empty binary tree be n0, n1 and n2 respectively, then n0 = n2 + 1
(the leaf node is one more than the second branch node)
If the total number of nodes in the tree is n, then
① n = n0 + n1 + n2 ② n = n1 + 2*n2 +1
Get: n0=n2+1
Property 2: there are at most m^(i-1) nodes in layer I of M-ary tree
There are at most m^(i-1) nodes in layer I of binary tree
Nature 3:

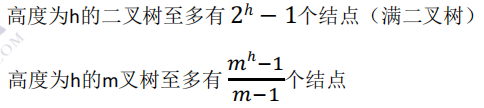
Common properties of complete binary trees

Nature 1:
Property 2: for a complete binary tree, the number of nodes with degrees 0, 1 and 2 can be deduced from the number of nodes n, and the number of nodes with degrees 0, 1 and 2 is n0, n1 and n2
A complete binary tree has at most one node with degree 1, that is, n1=0 or 1
If n0 = n2 + 1, n0 + n2 must be odd
Can be launched
If the complete binary tree has 2k (even) nodes, then
There must be n1=1, n0 = k, n2 = k-1
If the complete binary tree has 2k-1 (odd) nodes, then
There must be n1=0, n0 = k, n2 = k-1

Sequential storage of binary tree

#include <iostream>
using namespace std;
#define MaxSize 100
typedef int ElemType;

 struct TreeNode{
	ElemType value;
	bool IsEmpty;
};
 
 //Define an array, store the complete binary tree from top to bottom and from left to right in the array, and determine the child, parent and layer of the node according to the relative position of the subscript
 //If it is not a complete binary tree, it is stored in the corresponding position of the array according to the tree structure. This storage method causes a lot of waste of memory

int main()
{
	TreeNode tree[MaxSize];
}

Chain storage of binary tree

#include <iostream>
using namespace std;

#define MaxSize 100
typedef int ElemType;

typedef struct BiTNode {
	ElemType data;//Data domain
	struct BiTNode* lchild, * rchild;//Left child, right child
}BiTNode,*BiTree;
//The binary list with n nodes has n+1 empty chain fields
/*
* Access the node and print the value of the node
*/
void Visit(BiTNode *T)
{
	cout << T->data<< " ";
}
/*
* Preorder traversal 
*/
void PreOrder(BiTree T)
{
	if (T != NULL)
	{
		Visit(T);
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}
/*
* Medium order traversal
*/
void InOrder(BiTree T)
{
	if (T != NULL)
	{
		
		InOrder(T->lchild);
		Visit(T);
		InOrder(T->rchild);
	}
}
/*
* Postorder traversal
*/
void PostOrder(BiTree T)
{
	if (T != NULL)
	{

		PostOrder(T->lchild);
		PostOrder(T->rchild);
		Visit(T);
	}
}
/*
* Find the depth of the tree
*/
int treeDepth(BiTree T)
{
	if (T == NULL)
		return 0;
	int l = treeDepth(T->lchild);
	int r = treeDepth(T->rchild);
	return l > r ? l + 1 : r + 1;
}
int main()
{
	BiTree T;
	BiTNode* A, * B, * C, * D,*E,*F;
	T = (BiTree)malloc(sizeof(BiTNode));
	A = (BiTree)malloc(sizeof(BiTNode));
	B = (BiTree)malloc(sizeof(BiTNode));
	C = (BiTree)malloc(sizeof(BiTNode));
	D = (BiTree)malloc(sizeof(BiTNode));
	E= (BiTree)malloc(sizeof(BiTNode));
	F = (BiTree)malloc(sizeof(BiTNode));
	T->data = 1;
	A->data = 2;
	B->data = 3;
	C->data = 4;
	D->data = 5;
	E->data = 6;
	F->data = 7;
	T->lchild = A;
	T->rchild = B;
	A->lchild = C;
	A->rchild = D;
	B->lchild = E;
	B->rchild = F;
	C->lchild = NULL;
	C->rchild = NULL;
	D->lchild = NULL;
	D->rchild = NULL;
	E->lchild = NULL;
	E->rchild = NULL;
	F->lchild = NULL;
	F->rchild = NULL;
	cout << "Preorder traversal "; PreOrder(T); cout<< endl;
	cout << "Medium order traversal"; InOrder(T); cout << endl;
	cout << "Postorder traversal"; PostOrder(T); cout << endl;
	cout << treeDepth(T) << endl;
	return 0;
}

//Sequence traversal: using queues

//The binary tree is determined by the traversal sequence of first order, middle order and second order
//Need front + middle or rear + middle or layer + middle
//Two binary trees in the front, back and layer can not be uniquely determined
//

Trigeminal linked list

#include <iostream>
using namespace std;

#define MaxSize 100
typedef int ElemType;

typedef struct BiTNode {
	ElemType data;//Data domain
	struct BiTNode* lchild, * rchild;//Left child, right child
	struct BiTNode* parent;//Parent node
}BiTNode, * BiTree;
//The binary list with n nodes has n+1 empty chain fields
//The first in the middle and then in the arithmetic expression traversal corresponds to the prefix infix (delimiter required) suffix expression

Clue binary tree

#include <iostream>
using namespace std;

#define MaxSize 100
typedef int ElemType;

typedef struct ThreadNode 
{
	ElemType data;//Data domain
	struct ThreadNode* lchild, * rchild;//Left child, right child
	int ltag, rtag;//Left and right cue marks
}ThreadNode, * ThreadTree;

/*
* Middle order cueing of binary tree
*/
void CreateInThread(ThreadTree &T)
{
	ThreadTree pre = NULL;
	if (T != NULL)
	{
		InThread(T, pre);
		pre->rchild = NULL;//Process the last node
		pre->rtag = 1;
	}
}
/*
* Middle order cueing
*/
void InThread(ThreadTree T, ThreadTree & pre)
{
	if (T != NULL)
	{
		InThread(T->lchild, pre);
		if (pre != NULL && T->lchild == NULL)
		{
			T->lchild = pre;
			T->ltag = 1;
		}
		if (T != NULL && pre->rchild == NULL)
		{
			pre->rchild = T;
			pre->ltag = 1;
		}
		pre = T;
		InThread(T->rchild, pre);
	}
}
/*
* Preorder cueing (solving the magic circle of love)
*/
void PreThread(ThreadTree T, ThreadTree& pre)
{
	if (T != NULL)
	{
		
		if (pre != NULL && T->lchild == NULL)
		{
			T->lchild = pre;
			T->ltag = 1;
		}
		if (T != NULL && pre->rchild == NULL)
		{
			pre->rchild = T;
			pre->ltag = 1;
		}
		pre = T;
		if(T->ltag==0)//Only when the left child is not cued can we visit the left child to solve the problem of turning the magic of love around
			PreThread(T->lchild, pre);
		PreThread(T->rchild, pre);
	}
}

/*
* Post order cueing (the magic of love will not turn around in the middle order and post order)
*/
void PostThread(ThreadTree T, ThreadTree& pre)
{
	if (T != NULL)
	{
		InThread(T->lchild, pre);
		InThread(T->rchild, pre);
		if (pre != NULL && T->lchild == NULL)
		{
			T->lchild = pre;
			T->ltag = 1;
		}
		if (T != NULL && pre->rchild == NULL)
		{
			pre->rchild = T;
			pre->ltag = 1;
		}
		pre = T;
	}
}
/*
* Find the first node traversed by the middle order in the subsequence with p as the root
*/
ThreadNode* FirstNode(ThreadNode* p)
{
	while (p->ltag == 0) p=p->lchild;
	return p;
}
/*
* Find the middle order traversal successor of P node in the middle order clue binary tree
*/
ThreadNode* NextNode(ThreadNode* p)
{
	if (p->rtag == 0) return FirstNode(p->rchild);//Find the leftmost lower node of the right subtree
	else return p->rchild;
}
/*
* access node 
*/
void Visit(ThreadNode* T)
{
	cout << T->data << " ";
}
/*
* Traverse the entire binary tree that has been cued
*/
void InOder(ThreadTree T)
{
	for (ThreadNode* p =FirstNode(T); p != NULL; p = NextNode(p))
	{
		Visit(p);
	}
}
/*
* Find the last node traversed by the middle order in the subsequence with p as the root
*/
ThreadNode* LastNode(ThreadNode* p)
{
	while (p->rtag == 0) p = p->rchild;
	return p;
}
/*
* Find the middle order traversal precursor of P node in the middle order clue binary tree
*/
ThreadNode* PreNode(ThreadNode* p)
{
	if (p->ltag == 0) return LastNode(p->lchild);//Find the leftmost lower node of the right subtree
	else return p->lchild;
}
/*
* Reverse middle order traversal of the whole binary tree that has been cued
*/
void InOder(ThreadTree T)
{
	for (ThreadNode* p = LastNode(T); p != NULL; p = PreNode(p))
	{
		Visit(p);
	}
}
//Find the antecedent successor in the antecedent clue binary tree: if the right child is the clue, the successor is the node pointed by the right child; Otherwise, according to the law of "root left and right", the successor is the left child, and if there is no left child, it is the right child
//Find the antecedent in the antecedent clue binary tree: you need to find the parent node of the node first!! General binary tree can't do it, trigeminal linked list can.
//If the current node has a left brother, the precursor is the left brother, otherwise it is the parent node. If there is no parent node (the current node is the root node), there is no precursor.
//Find the last traversed node in the preorder clue binary tree: first look to the right from the root node. Look to the left only when you find a point without a right node but with a left node. Otherwise, look to the right whenever you meet a point with a right node

//Find the antecedent in the binary tree of sequential clues: if the left child is the clue, the antecedent is its reference; Otherwise, according to the principle of "left and right roots", the precursor of the current node is its right child, and if the right child is empty, it is the left child
//Find the postorder successor in the postorder clue binary tree: if the right child is the clue, the successor is its reference; Otherwise, the general binary tree cannot be found, and the trigeminal linked list can. If the current node is its husband's right child, the successor is its parent node;
//If the current node is the parent's left child and the parent has no right child, the node will be the parent node;
//If the current node is the left child of its father and its father has a right child, then its successor will be the lower left element of the right brother (always look to the bottom left, if there is a right child but no left child, then look to the right. If there is a left child on the way, still look to the left)

Storage structure of tree

1. Parental representation

#include <iostream>
using namespace std;
typedef int ElemType;
#define MaxSize 100
typedef struct {
	ElemType data;
	int parent;//Point to the parent node location, - 1 indicates the root node
}PTNode;
typedef struct {
	PTNode nodes[MaxSize];
	int n;//Node number
};
//The parent representation is relatively simple to find the parent node, but the child can only be traversed

2. Child representation

#include <iostream>
using namespace std;
#define MaxSize 100
typedef int ElemType;
struct CTNode {
	int child;
	struct CTNode* next;
};
typedef struct {
	ElemType data;
	CTNode* FirstNode;
}CTBox;
typedef struct {
	CTBox nodes[MaxSize];
	int n,r;//n node number, r root position
}CTree;

3. Representation of children's brothers

#include<iostream>
using namespace std;

typedef int ElemType;
typedef struct CSNode{
	ElemType data;//Data domain
	struct CSNode* firstchild, * nextsibling;//The first child, the brother of the first child
}CSNode,*CSTree;
//It is applied in the transformation of tree and binary tree

Binary sort tree

#include<iostream>
using namespace std;

#define MaxSize 100
typedef int ElemType;
typedef struct BSNode{
	ElemType key;
	struct BSNode* lchild, * rchild;
}BSTNode,*BSTree;
/*
* Binary sort tree search, return value e node
*/
BSTNode* BST_Search(BSTree T, ElemType e)
{
	while (T!=NULL&&T->key != e)
	{
		if (T->key > e)
			T = T->lchild;
		else
			T = T->rchild;
	}
	return T;
}
/*
* Insertion of binary tree
*/
int BST_Insert(BSTree& T, ElemType e)
{
	if (T == NULL)//If the current tree is empty, the inserted node is the root node of the subtree
	{
		T = (BSTNode*)malloc(sizeof(BSTNode));
		T->key = e;
		T->lchild = NULL;
		T->rchild = NULL;
		return 1;
	}
	if (T->key == e)//The same value already exists in the tree, failed to insert
		return 0;
	if (T->key > e)//If the current node value is larger than that to be interpolated, the left subtree to be interpolated is inserted
	{
		return BST_Insert(T->lchild, e);
	}
	else //If the current node value is smaller than that to be interpolated, the right subtree to be interpolated is inserted
		return BST_Insert(T->rchild, e);
	
}
/*
* Establish a binary sort tree according to the given array order
*/
void Create_BST(BSTree& T, ElemType a[], int n)//n is the number of array elements
{
	T = NULL;//Initially, the tree is empty
	int i = 0;
	while (i < n)//Insert the elements in the array into the binary sort tree in turn
	{
		BST_Insert(T, a[i]);
		i++;
	}
}
//Deletion of binary sort tree: 1 If the currently deleted node has only a left subtree or only a right subtree, it can be directly connected with the subtree after deleting the node
//2. If the currently deleted node has both left and right subtrees, it can be replaced by the direct successor (the minimum value in the right subtree) or the direct precursor (the maximum value in the left subtree) of the current node,
//The substitution method can be regarded as copying the substitution node value to the current node. Since the substitution node is the maximum value of the left subtree / the minimum value of the right subtree, there must be only the left subtree or the right subtree,
//At this time, it can be supplemented according to the method in 1
//Search length: the average search length ASL of keyword comparison times
/****************************************************************************************************************************/

balanced binary tree

Balanced binary tree: AVL
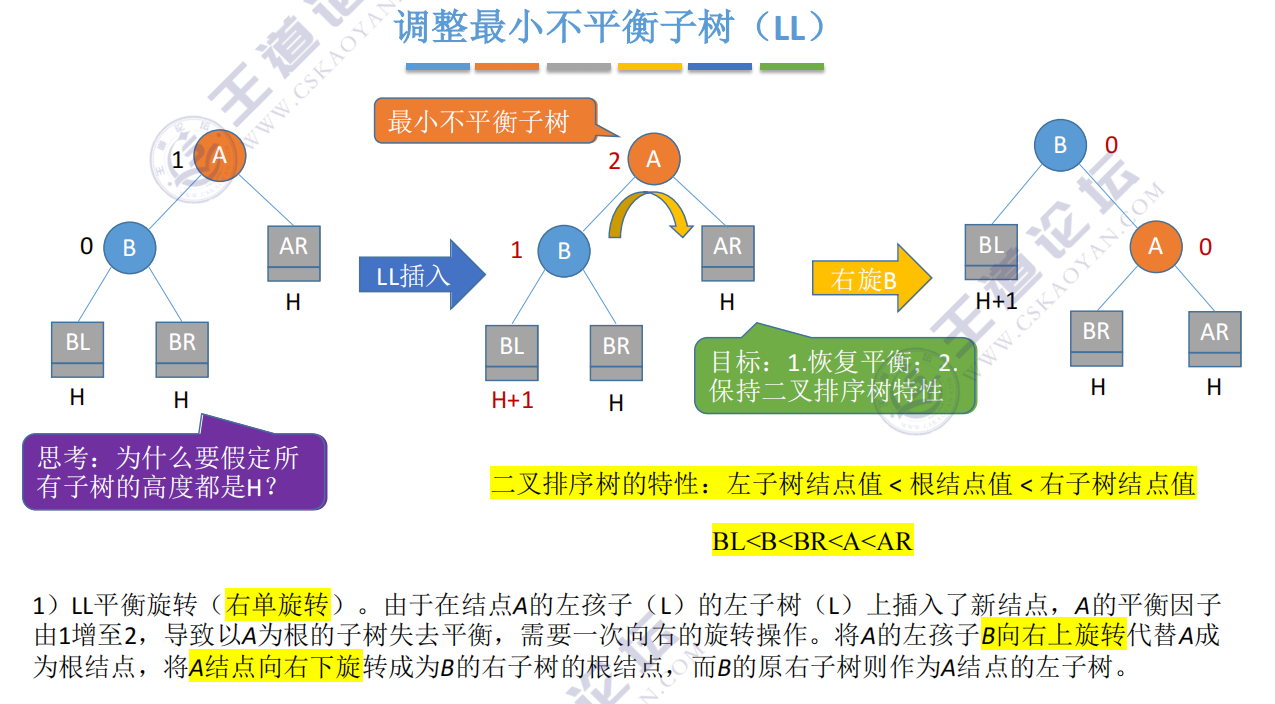
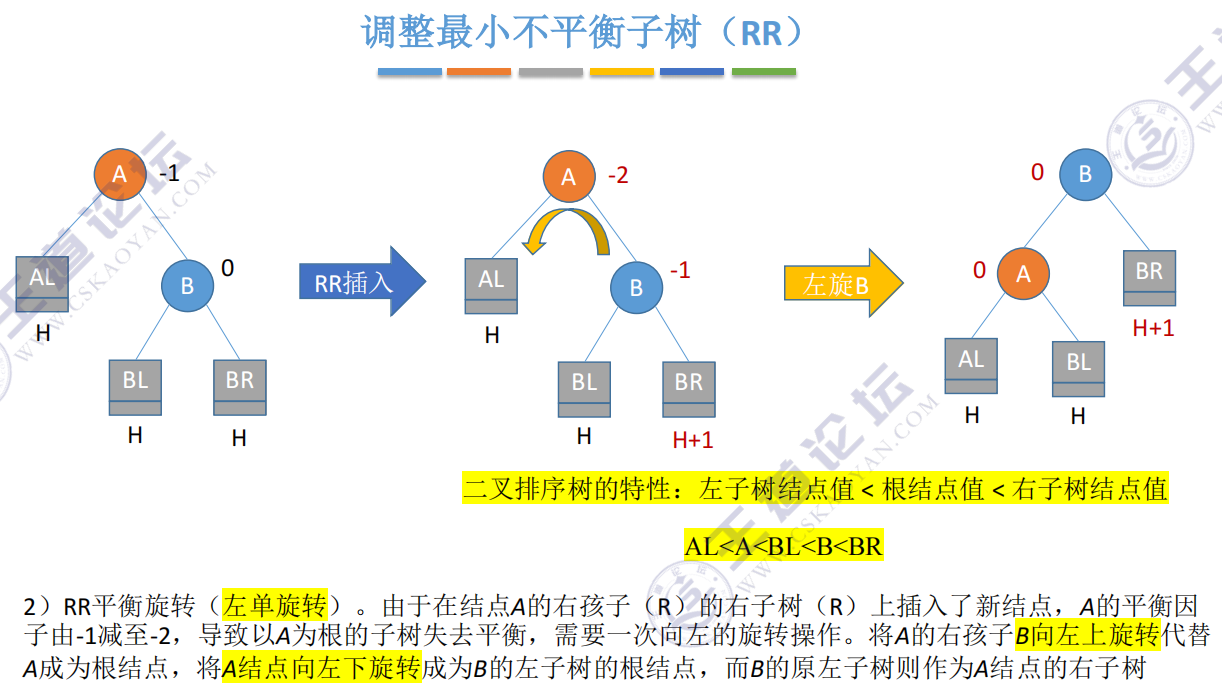
Node balance factor: left subtree height - right subtree height
Minimum unbalanced subtree: subtree of the first unbalanced node found from the insertion node
LL: inserting in the left subtree of the left child of A causes imbalance

RR: inserting in the right subtree of the right child of A causes imbalance

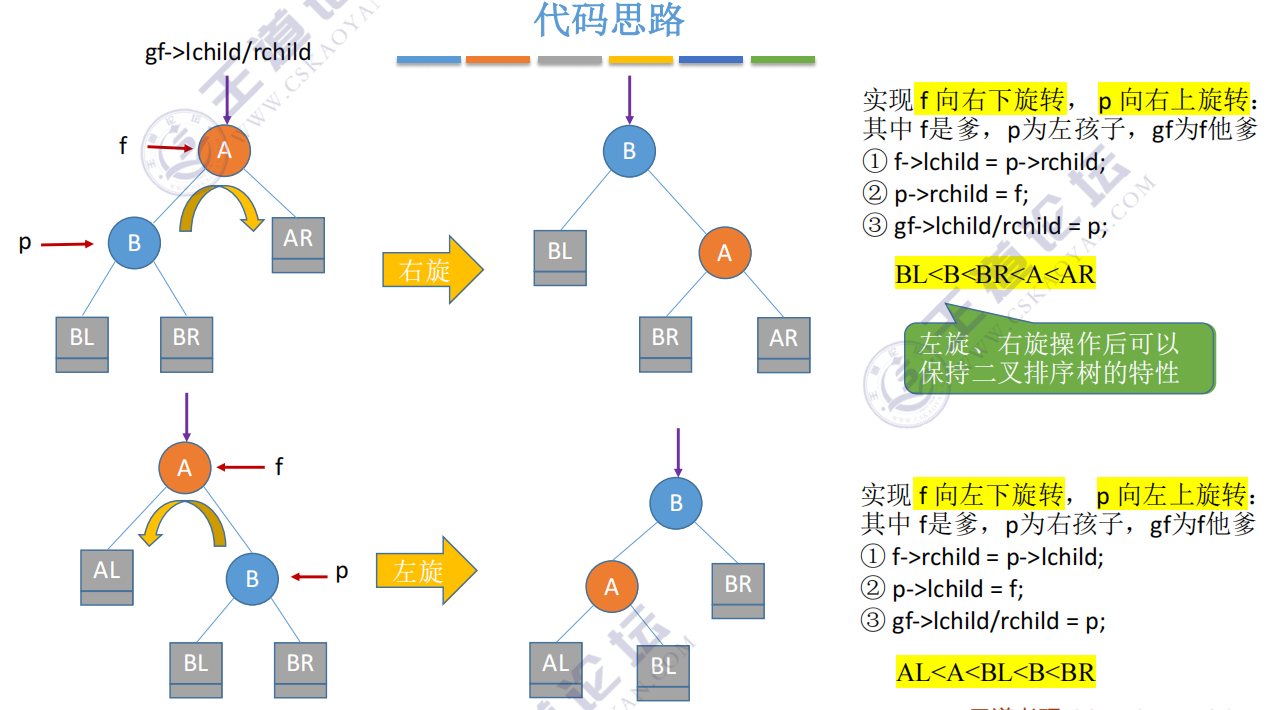
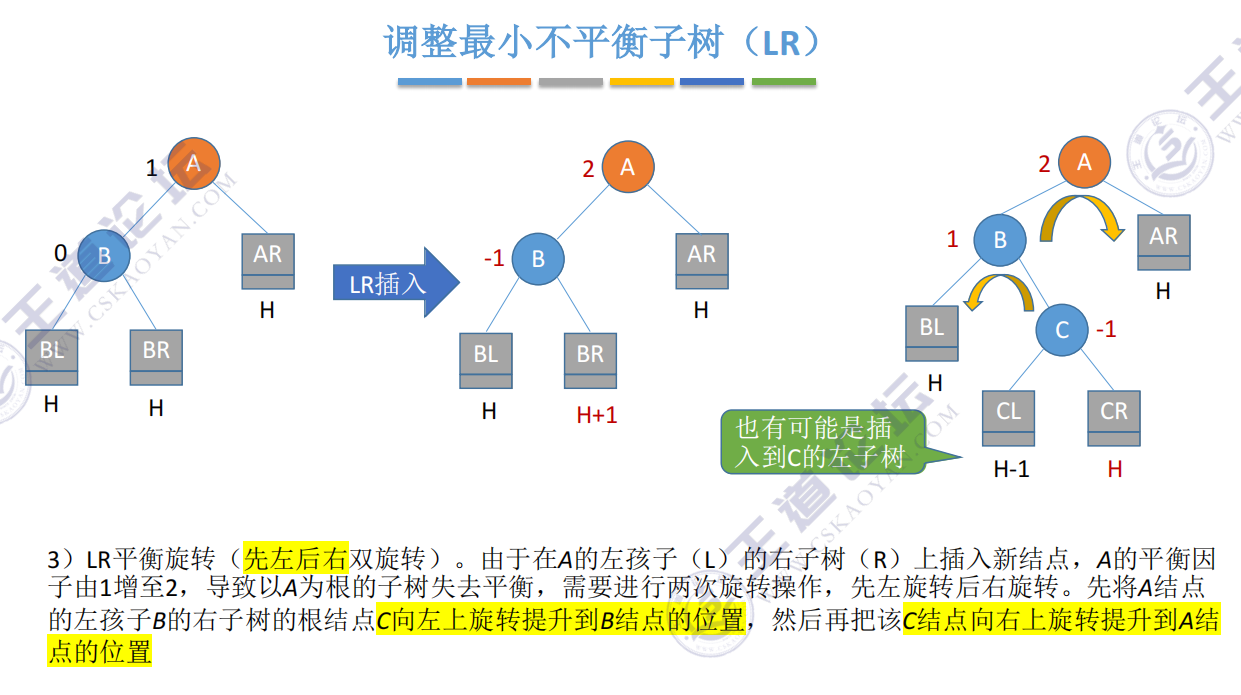
LR: inserting in the right subtree of the left child of A causes imbalance

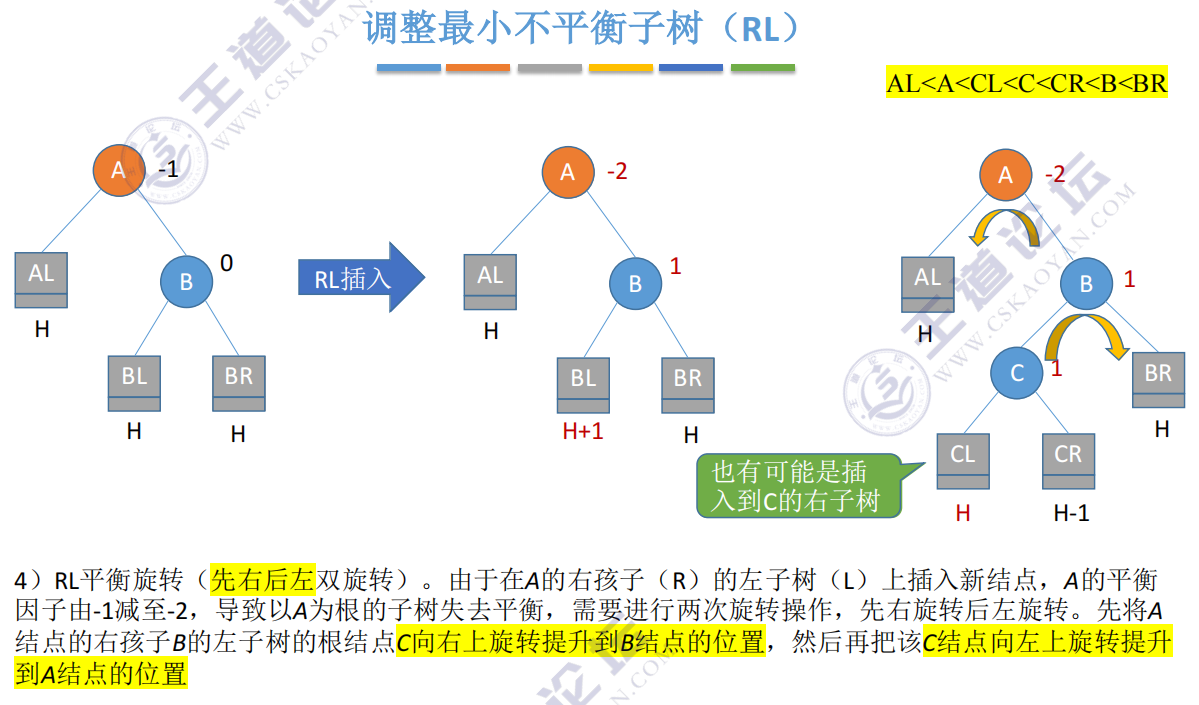
RL: inserting in the left subtree of the right child of A causes imbalance

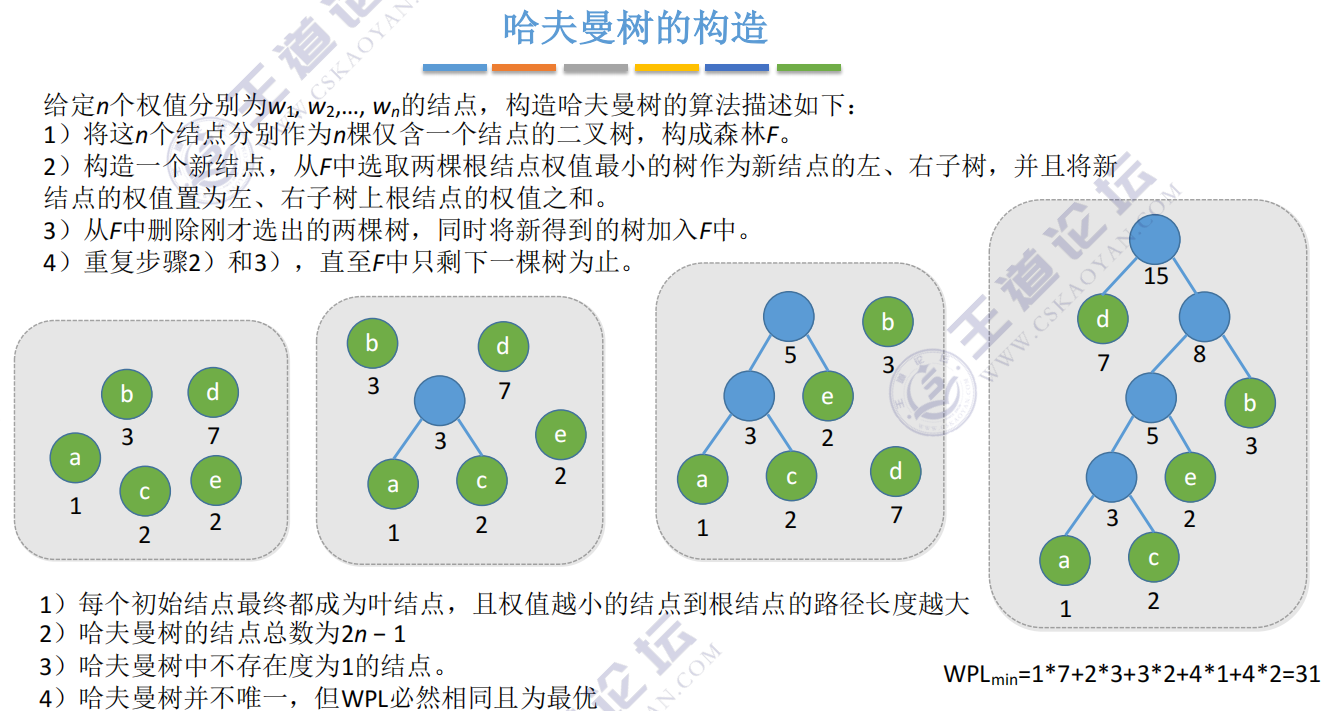
Huffman tree

Among the binary trees with n weighted leaf nodes, the binary tree with the smallest weighted path length (WPL) is called Huffman tree, also known as optimal binary tree