😉 Blog home page: Unlucky salad 🥗
💘 Welcome to pay attention 👍 comment 🏆 follow ⭐ ️
🏃 Stick together and grow together!
✏️ If there are mistakes in the article or you have better ideas, you can comment and point out, thank you!

0. There are words ahead
Learn the order of a data structure:
Logical structure - storage structure - operation and operation
According to this order, building a mind map in the brain will deepen memory ha!
1. Basic concept of stack
1.1 what is stack?
Stack is a linear table (also known as linear multinomial set) that can only be inserted or deleted at the same end.
From the concept, it is not difficult to see that the stack is actually a special linear table!
So where is it so special that we can discuss it as a new data structure?
1.2 why is the stack invincible?
Let's use examples in life to enter the stack:
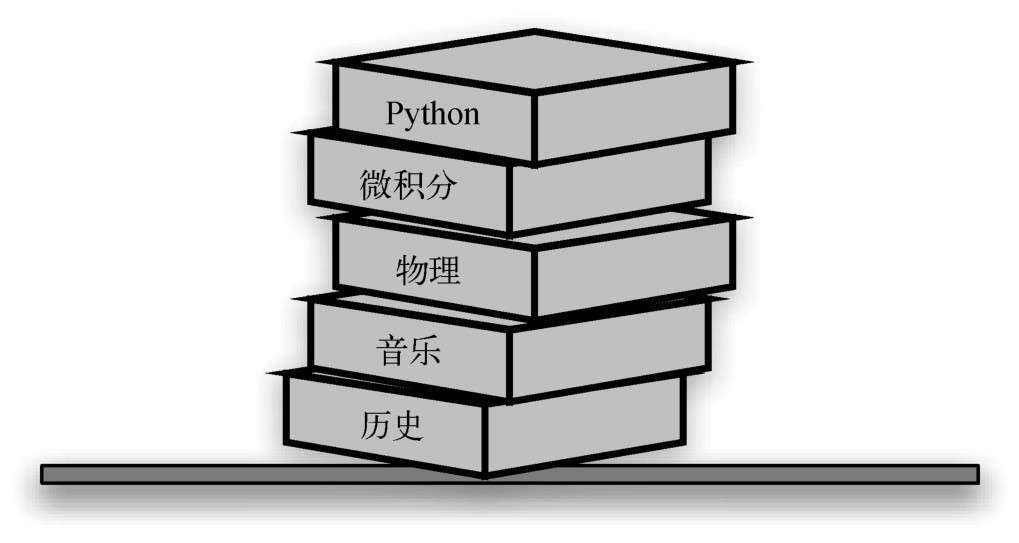
The above figure shows a stack of books. If they are stacked in this way, only the top Python will show the cover. When we want to get other books, we need to remove the books pressed on them one by one. In this way, some insignificant behaviors in life contain the main characteristics of the stack, namely "last in first out" or "first in first out", In other words, the elements of the last in stack are first out of the stack, so the stack is called the last in first out table.
Of course, in addition to this most important feature, there are some professional areas of the stack that we need to understand:
The end of the stack that allows insertion and deletion is called the top of the stack, and the other end is called the bottom of the stack;
When there are no data elements in the stack, it is called an empty stack (at this time, it is difficult to distinguish whether it is a stack or its big brother under the cloak of a linear table);
The insertion operation of stack is usually called stack entry, stack entry or push;
Deleting a stack is usually referred to as de stacking, out of stack, or pop-up.
After knowing all the above, we are getting started with the stack, but if we want to continue to work on the road of the stack, we have a long way to go, so we still need to continue to look down;
2. Storage structure and basic operation of stack
Since stack is a special linear table, when we talk about the storage structure of stack, do we think of the storage structure of linear table?
If you can, you still need to continue to see it;
2.1 sequential storage structure of stack
When the sequential storage structure is adopted, the stack that uses the list to store the elements in the stack is the sequential stack
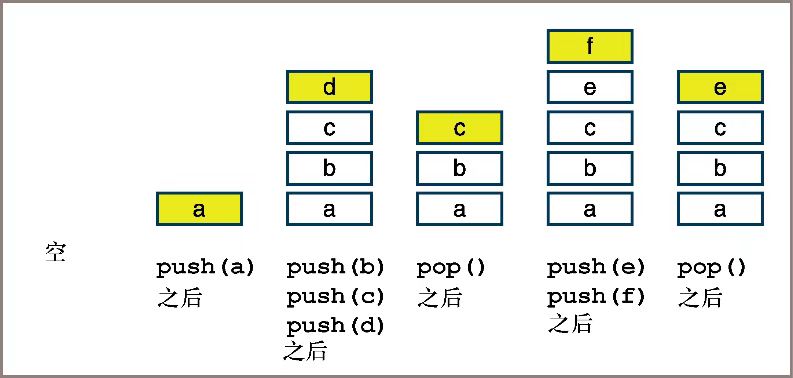
From the figure, we can summarize the four characteristics of sequential stack:
1) Stack empty condition: len(data)==0;
2) Stack full condition: in Python, the list can be expanded dynamically, so we don't need to consider stack full;
3) Stack entry: you can see from the above figure that the push() operation is used to add elements to the top of the stack;
4) Out of stack operation: the pop() method is used to delete the top element of the stack and return the element (pay attention to this if there is a return value!).
2.2 sequence stack for my use
The purpose of learning is to apply, so how can we use the sequence stack for us?

The above is a summary of some stack operations. Next, let's take a detailed look at the specific implementation of stack operations (with code):
1. Judge whether the stack is empty:
def isEmpty(self): if len(self.data)==0: #Judge whether the length of the list is 0 return True return False
2. Stacking:
def push(self,e): self.data.append(e)
The append method of the list is used to add the element to the top of the stack.
3. Out of stack:
def pop(self): return self.data.pop()
4. Get stack top element:
def peek(self): return self.data[-1]
2.3 chain storage structure of stack
The stack with chain storage is called chain stack.
By analogy with the four characteristics of sequential stack, we can get the chain stack:
1) Stack empty condition: head next==None;
2) Stack full condition: overflow on stack full does not need to be considered, which is also an advantage of chain stack;
3) Stack entry: use the push() method;
4) Stack out operation: use pop() method.
2.4 how to control the chain stack?
If a worker wants to do well, he must sharpen his tools first;
To skillfully use the chain stack, we must first understand the operation of the chain stack:
Don't run away and watch me operate!
1. Judge whether the stack is empty:
def isEmpty(self): if self.head.next==None: return True return False
2. Stacking:
def push(self,e): p=LinkNode(e) p.next=self.head.next self.head.next=p
3. Out of stack:
def pop(self): p=self.head.next self.head.next=p.next return p.data
4. Get stack top element:
def peek(self): return self.head.next.data
3. Some comprehensive applications of stack
1. Backtracking algorithm to solve maze problem
When it comes to the maze, I believe you may have played it when you were a child, including the honeycomb maze we have seen in the strongest brain;

In fact, the maze also has a long history. The maze first appeared in Knossos Palace on Crete, which is the center of Minoan civilization. Knossos palace is the center of politics and rituals. It is famous for its rooms, living space, exquisite murals indoors and outdoors, and a maze of highly decorative pottery.
Back to today's topic, with the help of stack, we use backtracking algorithm to solve maze problem;
What is the backtracking algorithm?
Take our own experience of playing the maze. When we come to an impassable Road, we will go back and choose another intersection again. The design of the backtracking algorithm comes from this consideration. When solving the maze problem, the computer adopts the traversal method. By traversing each intersection of the maze, when we encounter an impassable Road, we will remove the traversal like the operation of the stack, Re select another intersection, add the route to the stack every time, and finally form a path stack from the entrance to the exit; This is the design idea of our problem.
How do we represent the maze?
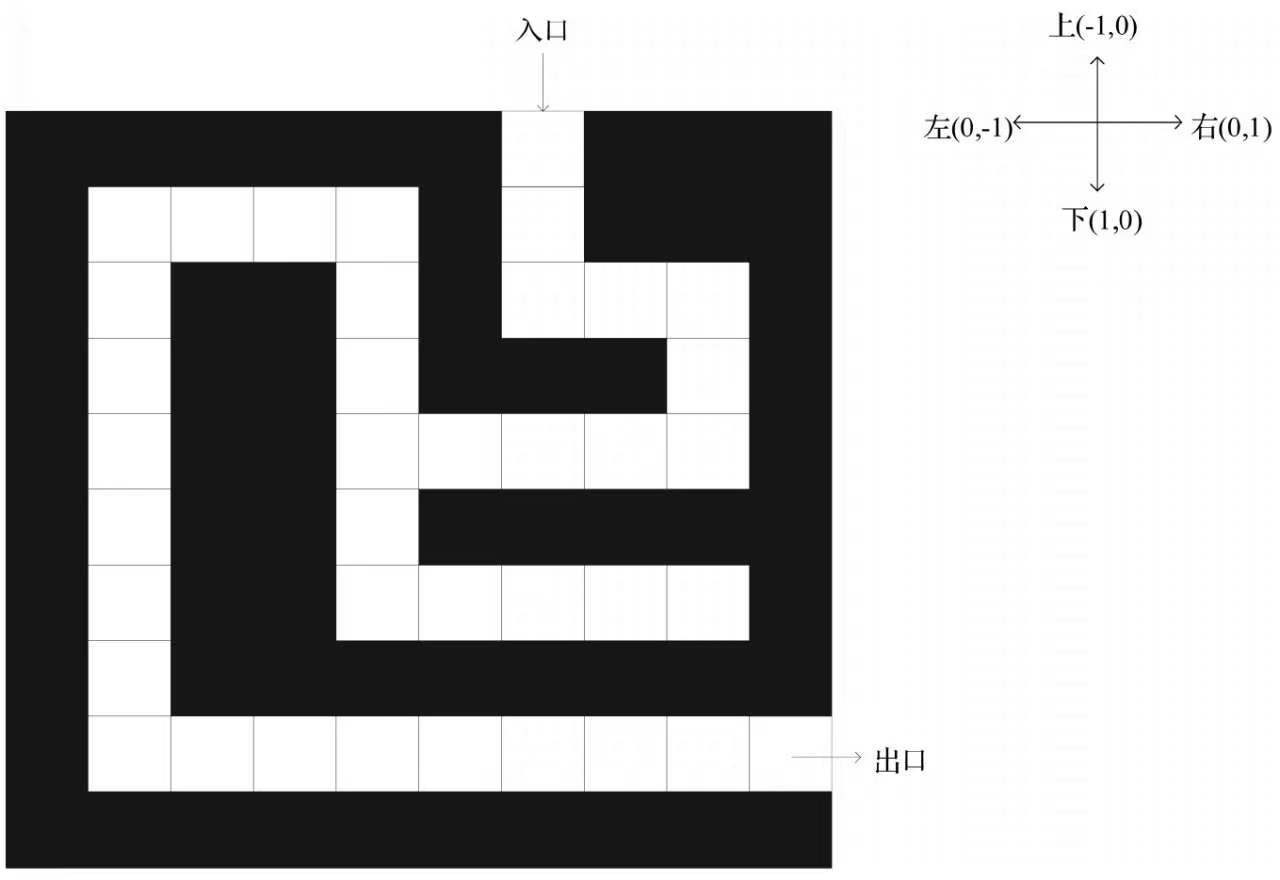
From the figure, we can see that the maze is composed of blocks. In this way, we can establish a two-dimensional list, with 0 representing white blocks (i.e. roads) and 1 representing black blocks (i.e. walls). In this way, because the entrance and exit are determined, we can regard them as walls, so we can express the maze as:
maze = [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 0, 0, 1, 0, 1, 1, 1],
[1, 0, 1, 1, 0, 1, 0, 0, 0, 1],
[1, 0, 1, 1, 0, 1, 1, 1, 0, 1],
[1, 0, 1, 1, 0, 0, 0, 0, 0, 1],
[1, 0, 1, 1, 0, 1, 1, 1, 1, 1],
[1, 0, 1, 1, 0, 0, 0, 0, 0, 1],
[1, 0, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
How to judge the direction?
When we solve the above problems, we should start to consider which direction we should choose in any position? In fact, the route design has been involved in considering this, but we should be clear that only the position marked as 0 can be taken. How should we choose among the four adjacent blocks up, down, left and right? This is the problem we need to solve in the second step; In this case, an offset is involved. First, we need to number each other's blocks;
The upper left corner is 0, and the horizontal 0 ~ 9 is x; Longitudinal 0-9 is y; Increase the number clockwise so that we can get the offset of X and y as follows:
dx=[-1,0,1,0] dy=[0,1,0,-1]
How to get out of the maze?
After we understand the above two problems, we will start to design the algorithm to get out of the maze;
Before formal design, we need to create a stack class and an orientation class;
class SqStack: #Stack class created
def __init__(self):
self.data=[]
def empty(self):
if len(self.data)==0:
return True
return False
def push(self,e):
self.data.append(e)
def pop(self):
assert not self.empty()
return self.data.pop()
def gettop(self):
assert not self.empty()
return self.data[-1]
class Box:
def __init__(self,i1,j1,di1):
self.i=i1
self.j=j1
self.di=di1
The establishment methods of these classes are involved in the above article;
Then we come to the most important part. We need to put the position coordinates of the current box into the stack from the entrance to the exit (given). We need to traverse four directions in turn to find the correct path. If we go to the wrong intersection, we will remove the top element of the stack according to the characteristics of the stack and explore another path;
The code is as follows:
def mazepath(xi,yi,xe,ye):
global maze #Make the maze array a global variable
maze = [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 0, 0, 1, 0, 1, 1, 1],
[1, 0, 1, 1, 0, 1, 0, 0, 0, 1],
[1, 0, 1, 1, 0, 1, 1, 1, 0, 1],
[1, 0, 1, 1, 0, 0, 0, 0, 0, 1],
[1, 0, 1, 1, 0, 1, 1, 1, 1, 1],
[1, 0, 1, 1, 0, 0, 0, 0, 0, 1],
[1, 0, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
st=SqStack() #Define a sequential stack
dx=[-1,0,1,0]
dy=[0,1,0,-1]
e=Box(xi,yi,-1) #Create entry box object
st.push(e) #Entry block stack
maze[xi][yi]=-1 #Set the stacked blocks to - 1 to avoid looking for adjacent blocks back and forth
while not st.empty():
b=st.gettop() #The block at the top of the stack is called the current block
if b.i==xe and b.j==ye:
for k in range(len(st.data)):
print("["+str(st.data[k].i)+','+str(st.data[k].j)+"]""\n",end=' ')
return True
find=False
di=b.di
while di<3 and find==False:
di+=1
i,j=b.i+dx[di],b.j+dy[di]
if maze[i][j]==0:
find=True
if find:
b.di=di
b1=Box(i,j,-1)
st.push(b1)
maze[i][j]=-1
else:
maze[b.i][b.j]=0
st.pop()
return False
xi,yi=1,6
xe,ye=8,8
print("Maze path is:",end=' ')
if not mazepath(xi,yi,xe,ye):
print("The maze has no solution")
Finally, splice the above codes together to get the solution path!

4. Write at the end
Here we are!
In a break, you can master all the foundations of the data structure stack. If you have time, you can also take a look at the title of the maze. Considering the length and complexity of the article, there are not too many dazzling pictures in the article, and the title is only a comprehensive application; However, this is not the final version. I will also improve the article according to my understanding at different stages, and add some new and interesting topics one after another!
If it's useful to you, give me a compliment before you go!
If you have any suggestions, you can comment on me!