This article is an original article of Joshua 317. Please note: reprinted from Joshua 317 blog Data structures and algorithms - linear search - binary search - Joshua 317's blog

1, Binary search description

Binary Search, also known as Binary Search, requires the data sequence to have a linear structure, that is, the sorted data sequence. For data sequences that have not been sorted, you can sort them first, and then perform a half search. It is an efficient search method. However, Binary Search has certain restrictions: the linear table must adopt sequential storage structure, and the elements in the table must be ordered by keywords (ascending or descending).

2, Binary search analysis

The basic idea of half search is:

In the ordered table, take the middle record as the comparison object

(1) If the value to be searched is equal to the value corresponding to the intermediate index, the search is successful.

(2) If the value corresponding to the intermediate index is greater than the value to be searched, continue searching in the first half of the intermediate index.

(3) If the value corresponding to the intermediate index is less than the value to be searched, continue searching in the second half of the intermediate index.

(4) Repeat the above search process until the search is successful or there is no value to be found in the ordered table, and the search fails.

The specific operation process is as follows:

Now we have an ordered integer array listData, and then set two variables, one is low, pointing to the position of the first index of the array, that is, low=0; The other is high, which points to the position of the last index of the array, that is: high=listData.length-1.

Set the value to find as value. When low ≤ high, repeat the following steps:

(1) Calculate the position mid of the intermediate index, mid = (low+high) / 2.

(2) Compare the value to be found with listData[middle].

① if listData[middle] == value, the search is successful, and the element referred to by middle is the element to be searched.

② if listdata [middle] > value, it means that if there is a value to be searched, the value must be in the first half of the search ordered array. Modify the upper bound of the search range: high=middle-1, turn to (1).

③ if listdata [middle] < value, it means that if there is a value to be searched, the value must be in the second half of the search ordered array. Modify the lower bound of the search range: low=middle+1, turn to (1).

Repeat the above process. When low > high, the search fails.

Next, let's divide the search process in the form of graphics and text:

Now there is an ordered set of integer data as {2, 12, 15, 23, 25, 28, 39, 40, 46, 66}

If you want to find a record with value=39, the half search process is as follows.

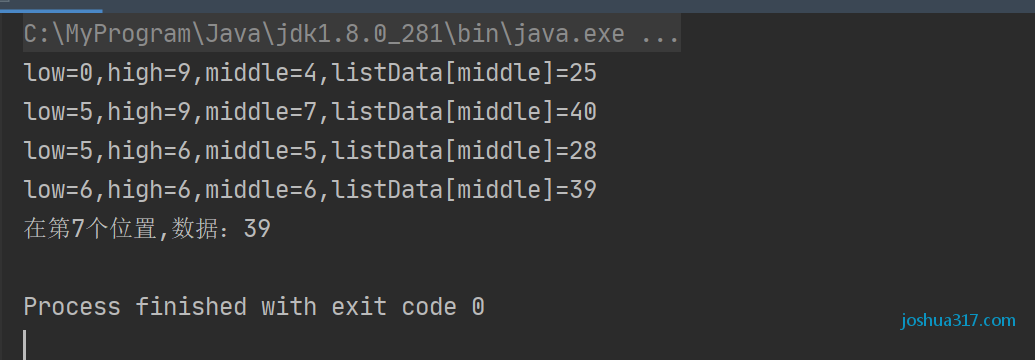
(1) Initial time

low=0；

high=9；

mid=(low+high)/2, middle=4;

listData[middle]=25；

(2) Compare listData[middle] and value. Since listData[middle] < 46, the next step is to find the second half, so

low=middle+1，low=5；

high Still 9, high=9；

mid=(low+high)/2, middle=7;

listData[middle]=40；

(3) Compare listData[middle] and value. Since listData[middle] > 39, the next step is to find the first half, so

low Still 5, low=5；

high=middle-1， high=6；

mid=(low+high)/2, middle=5;

listData[middle]=28；

(4) Compare listData[middle] and value. Since listData[middle] < 39, the next step is to find the second half, so

low=middle+1，low=6；
high Still 6, high=6；
mid=(low+high)/2，middle=6;
listData[middle]=39；

(5) Compare listData[middle] and value. Since listData[middle] == 39, the search is successful, the index is returned, and the end.

3, Implementation of binary search

package com.joshua317;

import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        /*
        System.out.println("Half search algorithm instance "");
        System.out.println("Please enter ten ordered integer data "");

        int[] listData = new int[10];
        Scanner scanner = new Scanner(System.in);
        // receive data 
        for (int i = 0; i < listData.length; i++) {
            listData[i] = scanner.nextInt();
        }

        // Print all array elements
        System.out.print("The input data is: ");
        for (int i = 0; i < listData.length; i++) {
            System.out.print(listData[i] + ",");
        }
        System.out.println();
        System.out.println("Please enter the data to find ");
        int value = scanner.nextInt();
         */
        int[] listData = {2, 12, 15, 23, 25, 28, 39, 40,46,66};
        int value = 39;

        int index = binarySearch(listData, value);
        if (index != -1) {
            System.out.println("In the first" + (index+1) + "Location,Data:" + listData[index]);
        } else {
            System.out.println("Data not found");
        }

    }

    public static int binarySearch(int[] listData, int value)
    {
        int low, middle, high;
        low = 0;
        high = listData.length - 1;
        while (low <= high) {
            middle = (low + high) / 2;
            System.out.printf("low=%d,high=%d,middle=%d,listData[middle]=%d", low, high, middle, listData[middle]);
            System.out.println();
            if (listData[middle] == value) {
                return middle;
            } else if (listData[middle] > value) {
                high = middle - 1;
            } else if (listData[middle] < value) {
                low = middle + 1;
            }
        }

        return -1;
    }
}

4, Finally

The advantages of half search are less comparison times than sequential search, faster search speed and higher execution efficiency. The disadvantage is that the storage structure of the table can only be sequential storage, not chain storage, and the elements in the table must be orderly. The average search length when the half search is successful is log2(n+1)-1, and its time complexity is O(log2n)

This article is an original article of Joshua 317. Please note: reprinted from Joshua 317 blog Data structures and algorithms - linear search - binary search - Joshua 317's blog