title: data structure and algorithm (I) sparse array and queue
date: 2021-11-26 21:08:27
tags: data structure and algorithm
1. Relationship between data structure and algorithm
(1) Data structure is a subject that studies the way of organizing data. With programming language, there will be data structure. Learning data structure well can write more beautiful and efficient code
(2) To learn data structure well, we should consider how to solve the problems encountered in life with programs
(3) Program = data structure + algorithm
(4) Data structure is the basis of the algorithm
2. Linear structure
(1) As the most commonly used data structure, linear structure is characterized by one-to-one linear relationship between data elements
(2) Linear structure has two different storage structures, namely sequential storage structure (array) and linked storage structure (linked list). A linear table with sequential storage is called a sequential table, and the storage elements in the sequential table are continuous
(3) A linear list with linked storage is called a linked list. The storage elements in the linked list are not necessarily continuous. The address information of data elements and adjacent elements are stored in the element node
(4) The common linear structures are: array, queue, linked list and stack
3. Nonlinear structure
Nonlinear structures include: two-dimensional array, multi-dimensional array, generalized table, tree structure and graph structure
4. Sparse array
4.1 first look at an actual demand
In Gobang game, it has the function of saving and connecting the board
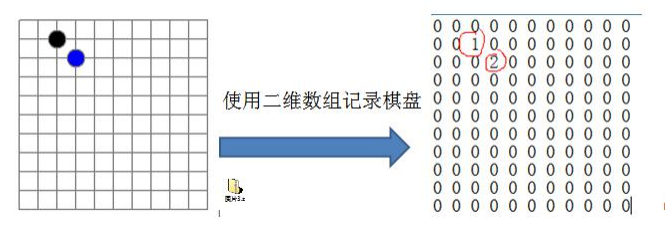
Because many default data of the two-dimensional array are 0, many meaningless data are recorded
When most elements in an array are 0 or the same value, you can use a sparse array to save the array
4.2 the processing method of sparse array is:
(1) How many rows and columns are there in the record array? How many different values are there
(2) The rows, columns and values of elements with different values are recorded in a small-scale array, so as to reduce the size of the data
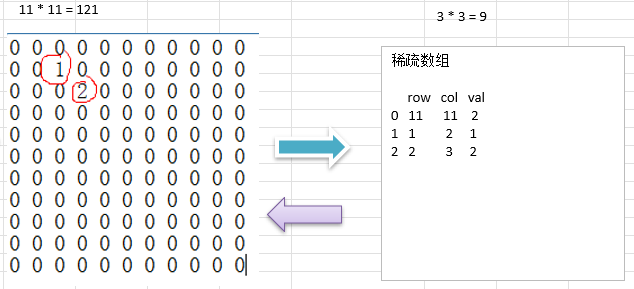
4.3 ideas
The idea of transforming two-dimensional array into sparse array
(1) Traverse the original two-dimensional array to get the number of valid data sum
(2) Based on sum, you can create a sparse array sparseArr int[sum + 1] [3]
(3) Store the valid data of the two-dimensional array into the sparse array
The idea of transforming sparse array into original two-dimensional array
(1) First read the first row of the sparse array and create the original two-dimensional array according to the data in the first row, such as chessArr2 = int [11][11] above
(2) After reading a few rows of data from the sparse array, assign it to the original two-dimensional array
Code implementation:
package com.cyk.sparsearray;
import java.io.*;
public class SparseArray {
public static void main(String[] args) {
// Create an original two-dimensional array 11 * 11
// 0: no chess pieces, 1: sunspots, 2: Lanzi
int chessArr1[][] = new int[11][11];
chessArr1[1][2] = 1;
chessArr1[2][3] = 2;
chessArr1[4][5] = 2;
// Output the original two-dimensional array
System.out.println("The original two-dimensional array is:");
for (int[] row : chessArr1) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
//Convert 2D array to sparse array
//1. First traverse the two-dimensional array to get the number of non-zero data
int sum = 0;
for (int i = 0; i < 11; i++) {
for (int j = 0; j < 11; j++) {
if (chessArr1[i][j] != 0) {
sum++;
}
}
}
//Create the corresponding sparse array
int sparseArr[][] = new int[sum + 1][3];
//Assign values to sparse arrays
sparseArr[0][0] = 11;
sparseArr[0][1] = 11;
sparseArr[0][2] = sum;
//Traverse the two-dimensional array and put non-zero data into the sparse array
int count = 0;//count is used to record the number of non-zero elements
for (int i = 0; i < 11; i++) {
for (int j = 0; j < 11; j++) {
if (chessArr1[i][j] != 0) {
count++;
sparseArr[count][0] = i;
sparseArr[count][1] = j;
sparseArr[count][2] = chessArr1[i][j];
}
}
}
//Output sparse array form
System.out.println();
System.out.println("The resulting sparse array is:");
for (int i = 0; i < sparseArr.length; i++) {
System.out.printf("%d\t%d\t%d\t\n", sparseArr[i][0], sparseArr[i][1], sparseArr[i][2]);
}
//TODO saves sparse arrays to a file
//TODO read sparse array
//Restore the sparse array to the original two-dimensional array
//1. First read the first row of the sparse array and create the original two-dimensional array according to the data of the first row
int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
//2. Then read the last few rows of data of the sparse array and assign it to the original two-dimensional array
for (int i = 1; i < sparseArr.length; i++) {
chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
//3. Output recovered 2D array
System.out.println();
System.out.println("The restored two-dimensional array is:");
for (int[] row : chessArr2) {
for (int data : row) {
System.out.printf("%d\t", data);
}
System.out.println();
}
}
}
5. Queue
5.1 queue introduction
(1) Queue is a sequential list, which can be implemented by array or linked list
(2) Follow the principle of first in, first out. That is, the data stored in the queue should be taken out first. After the deposit, it shall be taken out
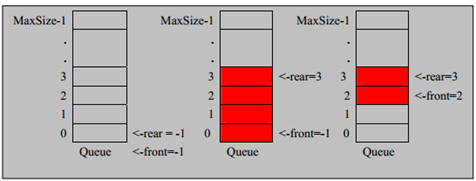
(3) Schematic: (use array to simulate queue schematic)
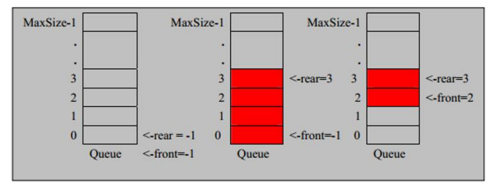
5.2 idea of array simulation queue
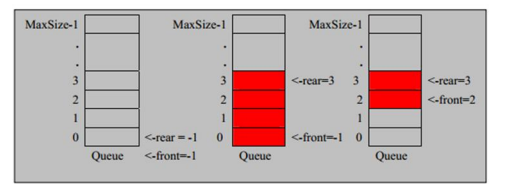
(1) The queue itself has a sequence table. If the array structure is used to store the data of the queue, the declaration of the queue array is shown in the figure below, where maxSize is the maximum capacity of the queue
(2) Because the output and input of the queue are processed from the front and rear ends respectively, two variables front and rear are required to record the subscripts at the front and rear ends of the queue respectively. The front will change with the data output, while the rear will change with the data input, as shown in the figure:
(3) When we store data in the queue, it is called "addQueue". The processing of addQueue needs two steps. Train of thought analysis:
① move the tail pointer back: rear+1. When front==rear, the queue is empty
② if the tail pointer rear is less than the maximum subscript maxSize-1 of the queue, the data will be stored in the data element indicated by rear, otherwise the data cannot be stored
When rear==maxSize-1, the queue is full
(4) Code implementation:
package com.cyk.queue;
import java.util.Scanner;
public class ArrayQueueDemo {
public static void main(String[] args) {
//Create a queue
ArrayQueue queue = new ArrayQueue(3);
char key = ' ';//Receive user input
Scanner scanner = new Scanner(System.in);
boolean flag = true;
while (flag) {
System.out.println("s(show): Displays all data for the queue");
System.out.println("e(exit): sign out");
System.out.println("a(add): Add data to queue");
System.out.println("g(get): Get queue data");
System.out.println("h(head): Displays the header data of the queue");
key = scanner.next().charAt(0);//Receive a character
switch (key) {
case 's':
queue.showQueue();
break;
case 'e':
scanner.close();
flag = false;
break;
case 'a':
System.out.println("Enter a number:");
int value = scanner.nextInt();
queue.addQueue(value);
break;
case 'g':
try {
int res = queue.getQueue();
System.out.printf("The extracted data are:%d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'h':
try {
int res = queue.headQueue();
System.out.printf("The data of the queue header is:%d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
default:
break;
}
}
System.out.println("Program exit");
}
}
//Simulating queues using arrays
class ArrayQueue {
private int maxSize;//Represents the maximum capacity of the array
private int front;//Queue header
private int rear;//Queue tail
private int[] arr;//This array is used to store data and simulate queues
//Create queue
public ArrayQueue(int arrMaxSize) {
maxSize = arrMaxSize;
arr = new int[maxSize];
front = -1;//Point to the queue header. front is the previous position pointing to the queue header
rear = -1;//Data pointing to the end of the queue (the last data of the queue)
}
//Determine whether the queue is full
public boolean isFull() {
return rear == maxSize - 1;
}
//Determine whether the queue is empty
public boolean isEmpty() {
return rear == front;
}
//Add data to queue
public void addQueue(int n) {
//Determine whether the queue is full
if (isFull()) {
System.out.println("The queue is full and data cannot be added");
return;
}
rear++;//Move rear
arr[rear] = n;
}
//Get the data of the queue and get out of the queue
public int getQueue() {
//Determine whether the queue is empty
if (isEmpty()) {
//Handling by throwing exceptions
throw new RuntimeException("The queue is empty and data cannot be retrieved");
}
front++;//front backward
return arr[front];
}
//Displays all data for the queue
public void showQueue() {
//ergodic
if (isEmpty()) {
System.out.println("Queue is empty");
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.printf("arr[%d]=%d\n", i, arr[i]);
}
}
//Displays the header data of the queue, not the fetched data
public int headQueue() {
//Judge whether it is empty
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
return arr[front + 1];
}
}
5.3 problem analysis and optimization
(1) At present, the array can no longer be used after being used once, which does not achieve the effect of taking
(2) Use the algorithm to improve this array into a ring queue (modulus:%)
5.4 array simulation ring queue
(1) The previous array simulates the optimization of the queue and makes full use of the array, so the array is regarded as a ring. (realized by taking mold)
(2) Analysis description:
① when the next index in the tail index is the header index, it indicates that the queue is full, that is, leave one queue capacity as the contract. When judging that the queue is full, you should pay attention to (rear + 1)% maxsize = = front (queue is full)
② rear == front (queue is empty)
③ analysis diagram:
(3) The idea is as follows:
① adjust the meaning of the front variable: front points to the first element of the queue, that is, arr[front] is the first element of the queue, and the initial value of front = 0
② adjust the meaning of the rear variable: rear points to the last element of the queue, because you want to make a space available as a convention, and the initial value of rear = 0
③ when the queue is full, the condition is (rear + 1)% maxsize = = front
④ for the condition that the queue is empty, rear == front (the queue is empty)
⑤ when we analyze in this way, the number of valid data in the queue (rear + maxsize - front)% maxsize / / rear = 1, front = 0
⑥ we can modify the original queue to get a ring queue
(4) Code implementation:
package com.cyk.queue;
import java.util.Scanner;
public class CircleArrayQueue {
public static void main(String[] args) {
//Create a ring queue
CircleArray queue = new CircleArray(4);//The maximum valid data for the queue is 3
char key = ' ';//Receive user input
Scanner scanner = new Scanner(System.in);
boolean flag = true;
while (flag) {
System.out.println("s(show): Displays all data for the queue");
System.out.println("e(exit): sign out");
System.out.println("a(add): Add data to queue");
System.out.println("g(get): Get queue data");
System.out.println("h(head): Displays the header data of the queue");
key = scanner.next().charAt(0);//Receive a character
switch (key) {
case 's':
queue.showQueue();
break;
case 'e':
scanner.close();
flag = false;
break;
case 'a':
System.out.println("Enter a number:");
int value = scanner.nextInt();
queue.addQueue(value);
break;
case 'g':
try {
int res = queue.getQueue();
System.out.printf("The extracted data are:%d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case 'h':
try {
int res = queue.headQueue();
System.out.printf("The data of the queue header is:%d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
default:
break;
}
}
System.out.println("Program exit");
}
}
//Simulating queues using circular arrays
class CircleArray {
private int maxSize;//Represents the maximum capacity of the array
private int front;//In the queue header, front points to the first element of the queue, that is, arr[front], and the initial value of front = 0
private int rear;//At the end of the queue, rear points to the next position of the last element of the queue, because you want to free up a space as a convention. The initial value of rear = 0
private int[] arr;//This array is used to store data and simulate queues
//Create queue
public CircleArray(int arrMaxSize) {
maxSize = arrMaxSize;
arr = new int[maxSize];
front = 0;
rear = 0;
}
//Determine whether the queue is full
public boolean isFull() {
return (rear + 1) % maxSize == front;
}
//Determine whether the queue is empty
public boolean isEmpty() {
return rear == front;
}
//Add data to queue
public void addQueue(int n) {
//Determine whether the queue is full
if (isFull()) {
System.out.println("The queue is full and data cannot be added");
return;
}
//Add data directly
arr[rear] = n;
//Move the rear, and here you must consider taking the mold
rear = (rear + 1) % maxSize;
}
//Get the data of the queue and get out of the queue
public int getQueue() {
//Determine whether the queue is empty
if (isEmpty()) {
//Handling by throwing exceptions
throw new RuntimeException("The queue is empty and data cannot be retrieved");
}
//1. First save the value corresponding to front to a temporary variable. If you return it directly, there will be no chance for front to move back
int value = arr[front];
//2. When moving the front backward, take the mold into consideration
front = (front + 1) % maxSize;
//3. Return temporarily saved variables
return value;
}
//Displays all data for the queue
public void showQueue() {
//ergodic
if (isEmpty()) {
System.out.println("Queue is empty");
return;
}
for (int i = front; i < front + size(); i++) {
System.out.printf("arr[%d]=%d\n", i % maxSize, arr[i % maxSize]);
}
}
//Find the number of valid data in the current queue
public int size() {
return (rear + maxSize - front) % maxSize;
}
//Displays the header data of the queue, not the fetched data
public int headQueue() {
//Judge whether it is empty
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
return arr[front];
}
}