566. Reshaping the matrix

Title Description

In MATLAB, there is a very useful function reshape, which can reshape an m x n matrix into another new matrix with different size (r x c), but retain its original data.

Give you an m x n matrix represented by a two-dimensional array mat, and two positive integers r and c, which respectively represent the number of rows and columns of the matrix you want to reconstruct.

The reconstructed matrix needs to fill all elements of the original matrix in the same row traversal order.

If the reshape operation with given parameters is feasible and reasonable, a new reshape matrix is output; Otherwise, the original matrix is output.

Example 1:

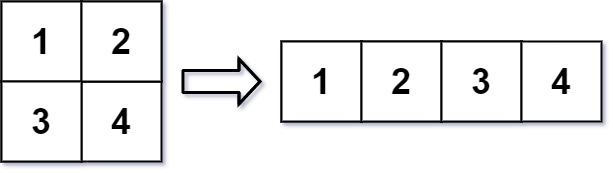
Input: mat = [[1,2],[3,4]], r = 1, c = 4
 Output:[[1,2,3,4]]

Example 2:

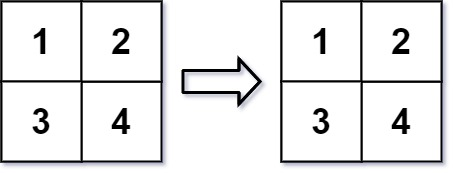
Input: mat = [[1,2],[3,4]], r = 2, c = 4
 Output:[[1,2],[3,4]]

Train of thought 1

This problem requires reshaping the matrix. The simple idea is to judge whether it can be reshaped directly according to whether the number of rows * columns before and after reshaping are equal. If it is not possible to reshape, return to the original matrix and start the assignment. The assignment process is realized by traversing the original matrix in two layers, which is identified by the horizontal and vertical coordinates of the reshaped matrix, and the reshaped matrix is assigned a value line by line, Until the current column is full, go to the next row, reset the column to 0, and repeat until the traversal is completed

Supplement of knowledge points:

C + + dynamic two-dimensional array (two-dimensional vector)

vector<vector<int>> mat(row,vector<int> (col));//Create a 2D array
//Get the number of rows and columns
int row=mat.size();//Get the number of rows
int col=mat[0].size();//Get the number of columns

Reference code

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
        int row=mat.size();//Get the number of rows
        int col=mat[0].size();//Get the number of columns
        //If the reshape operation of the given parameter is not feasible, the original matrix is output
        if(row*col!=r*c)
        {
            return mat;
        }
        //Otherwise: reshape the matrix
       vector<vector<int>> res(r,vector<int> (c));
       int ir=0,jc=0;//Horizontal and vertical subscripts of reshaped matrix
       for(int i=0;i<row;i++)
       {
           for(int j=0;j<col;j++)
           {
               //Assign a value to the transpose matrix row by row until the column is full, and then go to the next row
               if(jc>=c)
               {
                    jc=0;
                    ir++;
               }
               res[ir][jc++]=mat[i][j];
           }
       }
       return res;
    }
};

Idea 2 (array mapping method)

For a two-dimensional array with row number m, column number n and row and column subscripts numbered from 0, map each element (i, j) into the integer field, and they correspond to each integer in [0, mn) one by one according to the order of row priority.
Mapping two-dimensional array to one-dimensional array: (i,j) → i × n+j
Conversely, the integer i is mapped back to the subscript of the matrix (let the number of matrix columns be n):
Abscissa: i=x / n
Ordinate: J = x% n
This problem is to map the original array into a one-dimensional array first, and then map the one-dimensional group back to the two-dimensional array of r rows and n columns. Because the one-dimensional array is only a transitional effect, it can be omitted and mapped directly. You only need to traverse all subscripts 0~row*col (all subscripts of the original matrix converted into one-dimensional array)

res[i/c][i%c]=mat[i/col][i%col];

Reference code

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
        int row=mat.size();//Get the number of rows
        int col=mat[0].size();//Get the number of columns
        //If the reshape operation of the given parameter is not feasible, the original matrix is output
        if(row*col!=r*c)
        {
            return mat;
        }
        //Otherwise: reshape the matrix
       vector<vector<int>> res(r,vector<int> (c));
        //The integer x is mapped back to a two-dimensional array (realized by division and the number of remainder columns): the abscissa and ordinate i=x/col;j=x%col
      for(int i=0;i<row*col;i++)
      {
          res[i/c][i%c]=mat[i/col][i%col];
      }
       return res;
    }
};

118. Yanghui triangle

Title Description

Given a nonnegative integer numRows, the first numRows of the Yang Hui triangle are generated.

In the Yang Hui triangle, each number is the sum of its upper left and upper right numbers.

Sample

input: numRows = 5
 output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

input: numRows = 1
 output: [[1]]

thinking

Through the observation of Yang Hui triangle, we can find that the number of elements in row i (i starts from 0) is i+1, the beginning and end of each row are 1, and other elements are the sum of the corresponding column of the previous row and the two elements of the previous column. Therefore, through traversal, dynamically change the number of elements in each row and assign values in real time.

Knowledge points

The two-dimensional array implemented by vector can change the row and column values by * * resize() * * method

//Define an array of row and col columns
vector<vector<int>> array(row);
for (i = 0; i < array.size(); i++)
    array[i].resize(col);

Reference code

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector <int>> res(numRows);
        for(int i=0;i<numRows;i++)
        {
            //resize(): change the number of actual elements.
            res[i].resize(i+1);//The number of elements is i+1, because the subscript i starts from 0
            for(int j=0;j<i+1;j++)
            {
                if(j==0||j==i) res[i][j]=1;//1 at the beginning and end
                else
                {
                    res[i][j]=res[i-1][j-1]+res[i-1][j];//The other is the sum of the corresponding column of the previous row element and the previous column
                }
            }
        }
        return res;


    }
};