Construct program logic

This is a comprehensive exercise of the language elements, branch structure and circular structure learned before.

The title is as follows:

Look for daffodils.

Description: narcissus number is also known as super perfect number. It is a three digit number. The sum of the cubes of the numbers in each digit is exactly equal to itself, for example: $1 ^ 3 + 5 ^ 3 + 3 ^ 3 = 153 $.

num=int(input("Please enter a three digit number:"))
bai=int(num/100)
shi=int((num-bai*100)/10)
ge=num%10
#print(bai,shi,ge)
if ge**3+shi**3+bai**3==num:
    print(f'{num}It's daffodils')
else:
    print(f'{num}Not daffodils')

The above program is based on the idea of writing C program before. In fact, Python has an easy-to-use operator / / division, so the program can be improved to the following:

num=int(input("Please enter a three digit number:"))

bai=num//100

shi=num//10%10

ge=num%10

#print(bai,shi,ge)

if ge**3+shi**3+bai**3==num:

    print(f'{num}It's daffodils')

else:

    print(f'{num}Not daffodils')

A hundred dollars and a hundred chickens.

Explanation: a hundred dollars and a hundred chickens is a question raised in the Suanjing: a chicken Weng is worth five, a chicken mother is worth three, and a chicken chick is worth three. When you buy a hundred chickens for a hundred dollars, ask the chicken owner, the chicken mother and the chicken chick? A rooster is 5 yuan, a hen is 3 yuan and a chick is 1 yuan. Buy 100 chickens with 100 yuan. Ask how many roosters, hens and chicks are there?

for i in range(1,20):

    for j in range(1,33):

        for k in range(1,101):

            if (i+j+k)==100 and i*5+j*3+k/3==100:

                print(f'cock{i}Chicken, hen{j}Chicken, chicken{k}only')

The above algorithm uses the method of violent enumeration. This method is only suitable for programs with small amount of computation.

CRAPS gambling game.

Description: CRAPS is a table gambling game in the United States. The game uses two dice. Players get points by shaking two dice. The simple rule is: if the player shakes the dice for the first time, if he shakes out 7 or 11 points, the player wins; If the player shakes out 2, 3 or 12 points for the first time, the dealer wins; Other points players continue to roll dice. If the player rolls out the points for the first time, the player wins; For other points, the player continues to dice until the winner is determined.

import random

counter=1

while True:

    print(f'The first{counter}Round:')

    num1=random.randint(1,7)

    num2 = random.randint(1, 7)

    print(f'The result of rolling the dice twice is:{num1},{num2}')

    if num1+num2==7 or num1+num2==11:

        print("Player wins!")

        break;

    elif num1+num2==2 or num1+num2==3 or num1+num2==11:

        print("Dealer wins!")

        break;

    else:

        print("continue")

    counter+=1

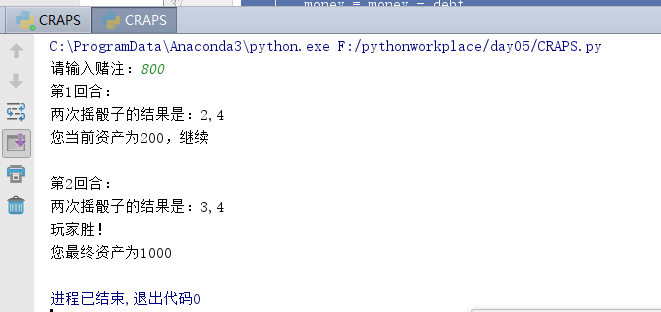
Improvement: add total assets and bets, and the procedure is improved as follows:

import random

counter=1

money=1000

debt=int(input("Please enter your bet:"))

while money>0:

    print(f'The first{counter}Round:')

    num1=random.randint(1,7)

    num2 = random.randint(1, 7)

    print(f'The result of rolling the dice twice is:{num1},{num2}')

    if num1+num2==7 or num1+num2==11:

        print("Player wins!")

        money = money + debt

        print(f'Your final assets are{money}')

        break;

    elif num1+num2==2 or num1+num2==3 or num1+num2==11:

        print("Dealer wins!")

        money = money - debt

        print(f'Your final assets are{money}')

        break;

    else:

        money = money - debt

        if money>0:

            print(f'Your current asset is{money}，continue')

        else:

            print("You're broke!")

        print()

    counter+=1

The first 20 numbers of the fichi series.

Note: the characteristic of Fibonacci sequence is that the first two numbers of the sequence are 1. Starting from the third number, each number is the sum of its first two numbers, such as 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 The program needs an intermediate variable c to temporarily store the value of a+b, and then a and B are updated respectively

a=1

b=1

print(a,end=" ")

for i in range(1,20):

    c=a+b

    a=b

    b=c

    print(a,end=" ")

Find the perfect number within 10000.

Note: perfect number is also called perfect number or complete number. The sum of all its true factors (i.e. factors other than itself) (i.e. factor function) is exactly equal to itself. For example, 6 ($6 = 1 + 2 + 3 $) and 28 ($28 = 1 + 2 + 4 + 7 + 14 $) are perfect numbers. How to store these factors? A variable result is used to store the sum of factors that can be adjusted each time.

import math

for i in range(2,10000):

    result=0

    for j in range(1,int(i/2)+1):

        if i%j==0:

            result+=j;

            #print(j)

    if result==i:

        print(i)

The above program is too violent. It takes a long time for the machine to get the result of 8128. It can be improved to:

import math

for num in range(2, 10000):

    result = 0

    for factor in range(1, int(math.sqrt(num)) + 1):

        if num % factor == 0:

            result += factor

            if factor > 1 and num // factor != factor:

                result += num // factor

    if result == num:

        print(num)

The idea of for factor in range(1, int(math.sqrt(num)) + 1) is to traverse only the factor with the square root of a certain number. The factor a greater than the square root always has a relationship that a*b is equal to the number with a factor b less than the square root. So if factor > 1 and num / / factor= Factor add one more judgment here to find the a corresponding to B.

Output all prime numbers within 100.

Note: prime refers to a positive integer (excluding 1) that can only be divided by 1 and itself.

for i in range(3,101):

    flag = True

    for j in range(2,i):

        if i%j==0:

            flag=False

            break;

    if flag:

        print(i,end=" ")