1.Debug mode
1.1 What is Debug mode
Is a program debugging tool for programmers. It can be used to view the execution process of a program or to track the execution of a program to debug it.
1.2 Debug introduction and operation process
-
How to add breakpoints
- Select the line of code where you want to set the breakpoint by clicking the left mouse button after the area of the line number
-
How to run programs with breakpoints
- Right-click Debug Execution in Code Area
-
See where
-
Look at the Debugger window
-
Look at the Console window
-
-
Where to point
- Point the Step Into (F7) arrow, or press F7 directly
-
How to Delete Breakpoints
-
Select the breakpoint you want to delete by clicking the left mouse button
-
If there are multiple breakpoints, you can click each one again. You can also delete them all at once
-
2.Binary Introduction and Writing Format
Introduction and Writing Format of 2.1 Binary
Code:
public class Demo1 {
/*
Decimal: In Java, numeric values are all 10 by default and do not require any modifications.
Binary: Values begin with 0b and can be in both case.
Octal: Numbers begin with 0.
Hexadecimal: Values begin with 0x and can be in both case.
Note: When writing, although binary identification is added, all the data printed on the console is decimal.
*/
public static void main(String[] args) {
System.out.println(10);
System.out.println("Binary Data 0 b10 The decimal representation of is:" + 0b10);
System.out.println("The decimal representation of octal data 010 is:" + 010);
System.out.println("Hexadecimal data 0 x10 The decimal representation of is:" + 0x10);
}
}
2.2 Conversion from Arbitrary to Decimal


2.3 Binary Conversion - Decimal to Arbitrary Conversion
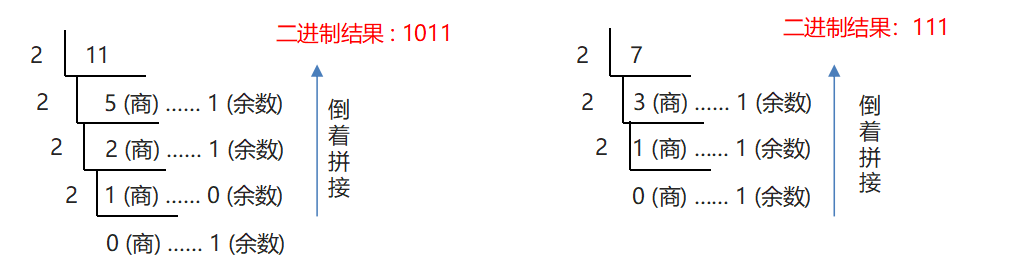
2.3.1: Conversion from decimal to binary
Formula: Divide base and use source data to get the remainder by dividing the base number (decimal, base number is a few) until quotient is 0, then spell the remainder upside down.
Requirement: Convert decimal number 11 to binary.
Implemented as follows: Source data is 11, using 11 to divide by cardinality continuously, that is, 2, until quotient is 0.
2.3.2: Conversion from decimal to hexadecimal
Formula: Divide base and use source data to get the remainder by dividing the base number (decimal, base number is a few) until quotient is 0, then spell the remainder upside down.
Requirement: Convert decimal number 60 to 16.
Implement this by dividing the base number by 60, or 16, until the quotient is 0.

Conclusion: Conversion from decimal to arbitrary
Formula: Divide base and use source data to get the remainder by dividing the radix (decimal, Radix is a few) until quotient is 0, then put the remainder upside down.
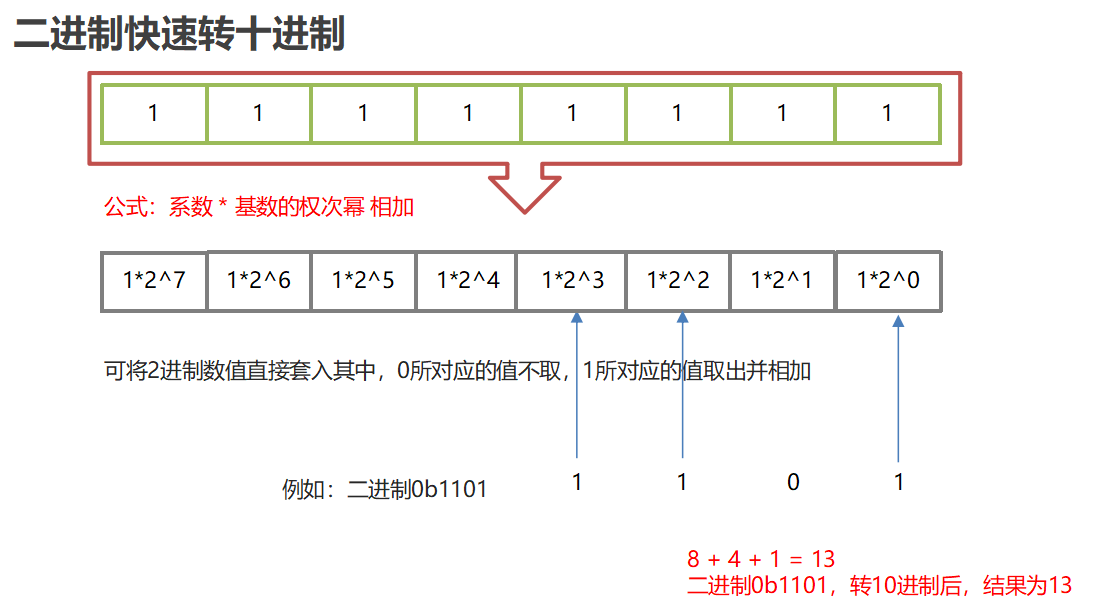
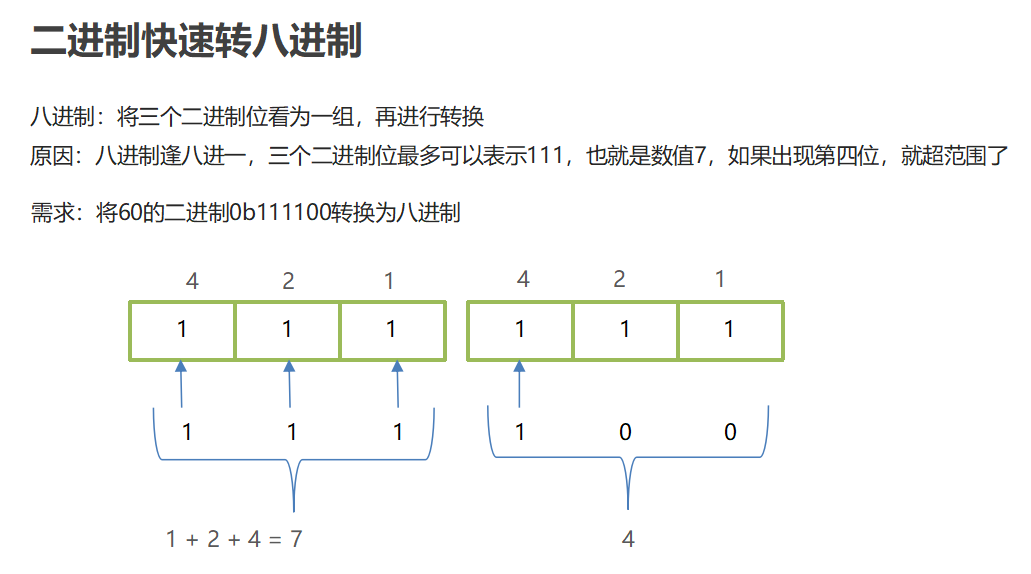
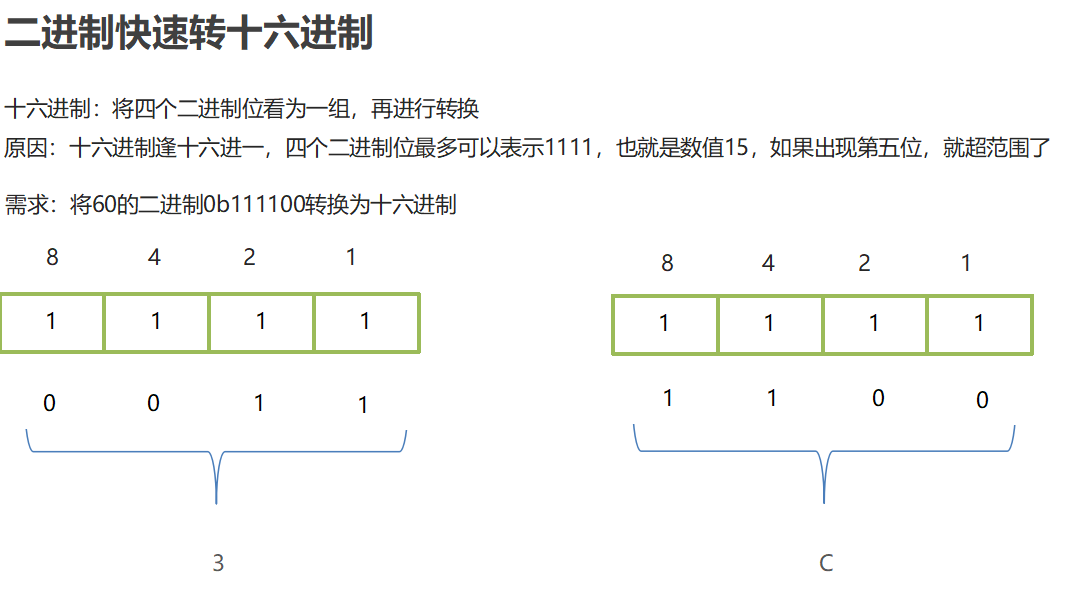
2.4 Fast Binary Conversion
8421 yards:
8421 code, also known as BCD code, is one of the most commonly used BCD codes: (Binary-Coded Decimal) Binary code decimal number In this encoding method, each binary value of 1 represents a fixed number, the result of adding the decimal number represented by each bit of 1 together is the decimal number it represents.
2.5 Original Code Reverse Complement
Foreword: The data in the computer is operated in the form of binary complement, which is deduced from the inverse code and the original code.
Source: (data size can be visualized)
It is a binary fixed-point representation, where the highest bit is the sign bit, [0] is positive, [1] is negative, and the rest is the size of the value.
+7 and -7 in one byte, code: byte b1 = 7; byte b2 = -7; A byte equals eight bits, or eight binary bits
0 (symbol bit) 0000111
1 (Symbol bit) 0000111
Inverse code: The inverse code of a positive number is the same as its original code; The inverse code of a negative number is a bit-by-bit reversal of its source code, except for the sign bits.
Complement code: (data is operated on in this state) The complement of a positive number is the same as its original code; The complement of a negative number is to add 1 at the end of its inverse code.


2.6 Bit Operations-Basic Bit Operators
package com.itheima.demo;
public class Demo2 {
/*
Bit operation:
Bit operators refer to the operation of binary bits, where decimal numbers are converted to binary before they are processed.
In binary bit operations, 1 is true and 0 is false.
& Bit and: false for false, 0 for zero
00000000 00000000 00000000 00000110 // 6 Binary
& 00000000 00000000 00000000 00000010 // 2 Binary
-----------------------------------------
00000000 00000000 00000000 00000010 // Result: 2
| Bit or: true when true, 1 when 1
^ Bitwise XOR: same false, different true
~ Reverse: Reverse all, 0 to 1, 1 to 0 (also including symbol bits)
00000000 00000000 00000000 00000110 // 6 Binary complement
~ 11111111 11111111 11111111 11111001
- 1 // -1 Inverse Code
------------------------------------
11111111 11111111 11111111 11111000 // Reverse Code Pushing
10000000 00000000 00000000 00000111 // -7
*/
public static void main(String[] args) {
System.out.println(6 & 2);
System.out.println(~6);
}
}
2.7-bit operation-displacement operator
Overview of Bit Operations: Bit operators refer to the operation of binary bits, which convert decimal numbers to binary before performing operations. In binary bit operations, 1 is true and 0 is false.
Introduction to bit operators: 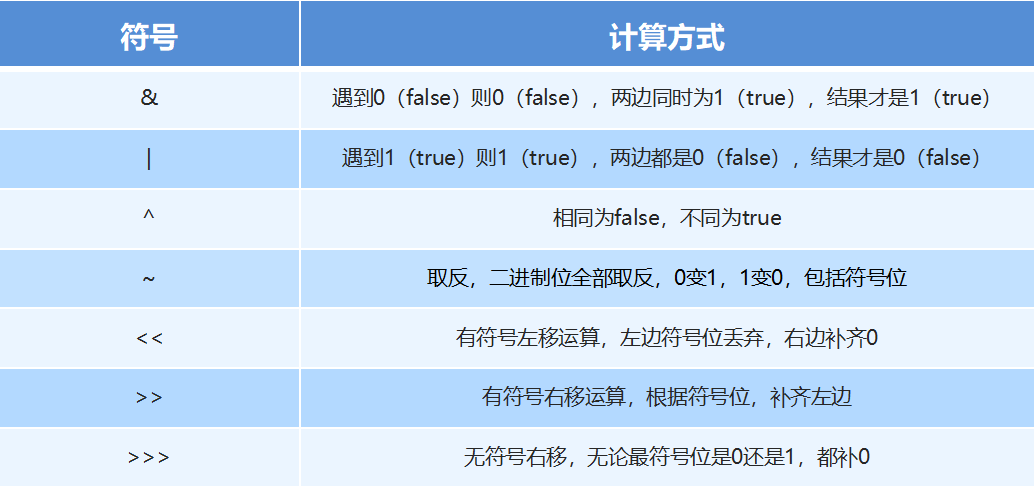
Code:
package com.itheima.demo;
public class Demo3 {
/*
Displacement operator:
<< Signed Left Shift, Binary Bit Left Shift, Left Symbol Bit Discarded, Right Complement 0
Rule of operation: Move a few bits to the left, that is, multiply by two powers
12 << 2
(0)0000000 00000000 00000000 000011000 // 12 Binary
-----------------------------------------------------------------------------
>> Signed Right Shift, Binary Bit Right Shift, Symbol Bit Complement
Rule of operation: Move a few bits to the right, that is, divide by two powers
000000000 00000000 00000000 0000001(1) // 3 Binary
-----------------------------------------------------------------------------
>>> Unsigned right shift operator, either 0 or 1, complements 0
010000000 00000000 00000000 00000110 // -6 Binary
*/
public static void main(String[] args) {
System.out.println(12 << 1); // 24
System.out.println(12 << 2); // 48
}
}
package com.itheima.demo;
public class Demo4 {
/*
^ Characteristics of Operators
One number, separated by another number, exclusive or twice, the number itself does not change
*/
public static void main(String[] args) {
System.out.println(10 ^ 5 ^ 10);
}
}
3. Basic Practices
3.1 Data Exchange
Case Requirements
Known as two integer variables a = 10, b = 20, use a program to exchange data between these two variables
The final output a = 20, b = 10;
code implementation
package com.itheima.test;
public class Test1 {
/*
Requirement: Known two integer variables a = 10, b = 20, use a program to exchange data between the two variables
The final output a = 20, b = 10;
Ideas:
1. Define a tripartite variable temp and give the value of a to the temp record (the value of a is not lost)
2. Use the a variable to record the value of b. (Once the first step is swapped, the value of b cannot be lost.)
3. Use the b variable to record the temp value, which is the original value of a (swap completed)
4. Output a and b variables
*/
/*
Dynamic Initialization Format:
Data type [][] variable name= new data type [m][n];
m Represents how many one-dimensional arrays this two-dimensional array can hold
n Represents how many elements can be stored in each one-dimensional array
*/
public static void main(String[] args) {
int a = 10;
int b = 20;
// Give the value of the original record of a to the temp record (the value of a will not be lost)
int temp = a;
// Record the value of b with a variable. (When the first step is swapped, the value of b cannot be lost.)
a = b;
// Use the b variable to record the temp value, which is the original value of a (swap completed)
b = temp;
// Output a and b variables
System.out.println("a=" + a);
System.out.println("b=" + b);
}
}
3.2 Array Inversion [Application]
Case Requirements:
An array arr is known = {19, 28, 37, 46, 50}; To exchange element values in an array programmatically,
Swapped array arr = {50, 46, 37, 28, 19}; And output the swapped array elements in the console
Steps to achieve:
1. Define two variables, start and end A pointer to start and end.
- Determine the exchange condition, start < end allows exchange
- Writing interchange logic code in a loop
- Each swap completes, changing the index start++, end-
- After the loop ends, iterate through the array and print to see the inverted array
Code implementation:
package com.itheima.test;
public class Test2 {
/*
Requirements: An array arr is known = {19, 28, 37, 46, 50}; To exchange element values in an array programmatically,
Swapped array arr = {50, 46, 37, 28, 19}; And output the swapped array elements in the console.
Steps:
1. Define two variables, start and end, to represent a pointer to start and end.
2. Determine the exchange condition, start < end allows exchange
3. Writing interchange logic code in a loop
4. Each swap completes, changing the index start++, end--to which the two pointers point
5. After the loop ends, iterate through the array and print to see the inverted array
*/
public static void main(String[] args) {
int[] arr = {19, 28, 37, 46, 50};
// 1. Define two variables, start and end, to represent a pointer to start and end.
int start = 0;
int end = arr.length -1;
// 2. Determine the exchange condition, start < end allows exchange
// 4. Change the index start++, end--
// for(int start = 0, end = arr.length -1; start < end; start++, end--)
for( ; start < end; start++, end--){
// 3. Write interchange logic code in a loop
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
}
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
3.3 Overview of 2-D Arrays
Overview: Two-dimensional arrays are also containers, unlike one-dimensional arrays, which store one-dimensional array containers
3.4 2D Array Dynamic Initialization
Dynamic Initialization Format: data type[][] Variable Name = new data type[m][n]; m Represents how many one-dimensional arrays this two-dimensional array can hold n Represents how many elements can be stored in each one-dimensional array
package com.itheima.demo;
public class Demo1Array {
/*
Dynamic Initialization Format:
Data type [][] variable name= new data type [m][n];
m Represents how many one-dimensional arrays this two-dimensional array can hold
n Represents how many elements can be stored in each one-dimensional array
*/
public static void main(String[] args) {
// Data type [][] variable name= new data type [m][n];
int[][] arr = new int[3][3];
/*
[[I@10f87f48
@ : Separator
10f87f48 : Hexadecimal memory address
I : Types of data stored in arrays
[[ : Several brackets represent a multidimensional array
*/
System.out.println(arr);
/*
When a two-dimensional array stores a one-dimensional array, it stores the memory address of the one-dimensional array
*/
System.out.println(arr[0]);
System.out.println(arr[1]);
System.out.println(arr[2]);
System.out.println(arr[0][0]);
System.out.println(arr[1][1]);
System.out.println(arr[2][2]);
// Storing elements in a two-dimensional array
arr[0][0] = 11;
arr[0][1] = 22;
arr[0][2] = 33;
arr[1][0] = 11;
arr[1][1] = 22;
arr[1][2] = 33;
arr[2][0] = 11;
arr[2][1] = 22;
arr[2][2] = 33;
// Remove elements from a two-dimensional array and print them
System.out.println(arr[0][0]);
System.out.println(arr[0][1]);
System.out.println(arr[0][2]);
System.out.println(arr[1][0]);
System.out.println(arr[1][1]);
System.out.println(arr[1][2]);
System.out.println(arr[2][0]);
System.out.println(arr[2][1]);
System.out.println(arr[2][2]);
}
}
Details of 3.5 2-D Array Access Elements
Question: Two-dimensional arrays store one-dimensional arrays. Can we store [pre-created one-dimensional arrays]?
A: Yes
code implementation
package com.itheima.demo;
public class Demo2Array {
/*
Question: Two-dimensional arrays store one-dimensional arrays. Can we store [pre-created one-dimensional arrays]?
A: Yes
*/
public static void main(String[] args) {
int[] arr1 = {11,22,33};
int[] arr2 = {44,55,66};
int[] arr3 = {77,88,99,100};
int[][] arr = new int[3][3];
arr[2][3] = 100;
arr[0] = arr1;
arr[1] = arr2;
arr[2] = arr3;
System.out.println(arr[1][2]);
System.out.println(arr[2][3]);
}
}
3.6 Two-dimensional Array Static Initialization
**Full Format :** data type[][] Variable Name = new data type[][]{ {Element 1, Element 2...} , {Element 1, Element 2...}
**Simplified Format :** data type[][] Variable Name = { {Element 1, Element 2...} , {Element 1, Element 2...} ...};
** Code implementation: **
package com.itheima.demo;
public class Demo3Array {
/*
Full format: data type [][] variable name = new data type [][]{element 1, element 2...}, {element 1, element 2...};
Simplified format: Data type [][] Variable name = {{Element 1, Element 2...}, {Element 1, Element 2...}...};
*/
public static void main(String[] args) {
int[] arr1 = {11,22,33};
int[] arr2 = {44,55,66};
int[][] arr = {{11,22,33}, {44,55,66}};
System.out.println(arr[0][2]);
int[][] array = {arr1,arr2};
System.out.println(array[0][2]);
}
}
3.7 Two-dimensional Array Traversal
Requirements:
It is known that a two-dimensional array arr = {{11, 22, 33}, {33, 44, 55};
Walk through the array, take out all elements, and print
Steps:
1. Traverse through the two-dimensional array, taking out each one-dimensional array inside 2. During the traversal process, the traversal continues for each one-dimensional array, obtaining each element stored internally
Code implementation:
package com.itheima.test;
public class Test1 {
/*
Requirements:
Known as a two-dimensional array arr = {{11, 22, 33}, {33, 44, 55};
Traverse the array, take out all elements, and print
Steps:
1. Traverse through the two-dimensional array, taking out each one-dimensional array inside
2. During the traversal process, the traversal continues for each one-dimensional array, obtaining each element stored internally
*/
public static void main(String[] args) {
int[][] arr = {{11, 22, 33}, {33, 44, 55}};
// 1. Traverse through a two-dimensional array and take out each one-dimensional array inside
for (int i = 0; i < arr.length; i++) {
//System.out.println(arr[i]);
// 2. During traversal, continue traversing each one-dimensional array to get every element stored internally
//int[] temp = arr[i];
for (int j = 0; j < arr[i].length; j++) {
System.out.println(arr[i][j]);
}
}
}
}
3.8 Sum of 2-D Arrays
Requirements:
The quarterly and monthly statistics for a company are as follows:(Ten thousand yuan) First quarter: 22,66,44 Second quarter: 77,33,88 Third quarter: 25,45,65 Fourth quarter: 11,66,99
Steps:
- Define summation variables and prepare to record the final cumulative result
- Use a two-dimensional array to store data, one-dimensional array for each quarter, and then assemble four one-dimensional arrays
- Traversing through a two-dimensional array, getting all the elements, summing them up
- Output Final Results
Code implementation:
package com.itheima.test;
public class Test2 {
/*
Requirements:
Quarterly and monthly statistics for a company are as follows: Units (RMB 10,000)
First quarter: 22,66,44
Second quarter: 77,33,88
Third quarter: 25,45,65
Quarter 4: 11,66,99
Steps:
1. Define summation variables and prepare to record the final cumulative result
2. Use a two-dimensional array to store data, one-dimensional array for each quarter, and then assemble four one-dimensional arrays
3. Traversing through a two-dimensional array, getting all the elements, summing them up
4. Output Final Results
*/
public static void main(String[] args) {
// 1. Define summation variables and prepare to record the final cumulative result
int sum = 0;
// 2. Use a two-dimensional array to store data, one-dimensional array for each quarter, and then assemble four one-dimensional arrays
int[][] arr = { {22,66,44} , {77,33,88} , {25,45,65} , {11,66,99}};
// 3. Traverse a two-dimensional array to get all the elements and sum them up
for (int i = 0; i < arr.length; i++) {
for(int j = 0; j < arr[i].length; j++){
sum += arr[i][j];
}
}
// 4. Output Final Results
System.out.println(sum);
}
}