2021.5.4

Title:

Given a string, please find the length of the longest substring that does not contain duplicate characters.

Example:

input: s = "pwwkew"
output: 3
 explain: Because the longest substring without duplicate characters is "wke"，So its length is 3.
     Please note that your answer must be the length of the substring,"pwke" It's a subsequence, not a substring.

Force buckle Title address:

https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/

Problem solving ideas:

The train of thought of this article is from the train of thought of big men

Step 1: solution 1

At first, we must think of using a function to judge whether the substring is repeated, and then use a function to cycle through all substrings to find the longest substring. The idea is no problem, but the three for loops will timeout when the data is large.

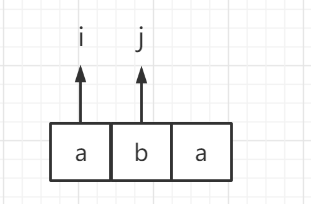
Illustration: i is actually equivalent to the left pointer and j is equivalent to the right pointer.

 

public int lengthOfLongestSubstring(String s) {
    int n = s.length();
    int ans = 0;//Save the maximum value of the substring that meets the conditions
    for (int i = 0; i < n; i++)
        for (int j = i + 1; j < n+1; j++) //The reason why j < n + 1 is that our substring is [i,j), closed on the left and open on the right. As in the above picture, the longest substring is 3, so j needs 1 more than it to be expressed
            if (allUnique(s, i, j)) ans = Math.max(ans, j - i); //Update ans
    return ans;
}

public boolean allUnique(String s, int start, int end) {
    Set<Character> set = new HashSet<>();//Initialize hash set
    for (int i = start; i < end; i++) {//Traverse each character
        Character ch = s.charAt(i);
        if (set.contains(ch)) return false; //Determine whether the character is in the set
        set.add(ch);//If not, add this character to set
    }
    return true;
}

Step 2: solution 2

Unfortunately, the above algorithm did not pass leetCode, and the time complexity was too large, resulting in timeout. How can we optimize it?

In the above algorithm, we assume that when i takes 0,

• j takes 1 to judge whether there are duplicate characters in the string str[0,1).
• j takes 2 to judge whether there are duplicate characters in the string str[0,2).
• j takes 3 to judge whether there are duplicate characters in the string str[0,3).
• j takes 4 to judge whether there are duplicate characters in the string str[0,4).

Did a lot of repetitive work, Because if there are no duplicate characters in str[0,1), we don't need to judge whether there are duplicate characters in the whole string str[0,2), but just judge whether str[2] is in str [0,1]. If it is not, it means that there are no duplicate characters in str[0,2). If it is, then str[0,3), str[0,4), str[0,5) there must be repeated characters, so the following j does not need to be added at this time. i + + can enter the next cycle.

In addition, our j does not need to take j + 1, but just start from the current J.

To sum up, in fact, the whole cycle about j can be completely removed. At this time, it can be understood that it has become a "sliding window".

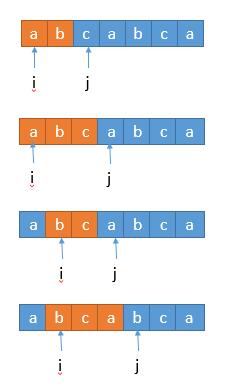
The whole is that the orange window is moving to the right in turn.

To judge whether a character is in the string or not, we need to be able to traverse the whole string. The time complexity required for traversal is O (n). Plus the loop of i in the outermost layer, the overall complexity is O (n) ²). We can continue to optimize and judge whether the character is in a string. We can save the existing string in Hash. In this way, the time complexity is O (1), and the total time complexity becomes o (n).

public class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length();
        Set<Character> set = new HashSet<>();
        int ans = 0, i = 0, j = 0;
        while (i < n && j < n) {
            if (!set.contains(s.charAt(j))){
                set.add(s.charAt(j++));
                ans = Math.max(ans, j - i);
            }
            else {
                set.remove(s.charAt(i++));
            }
        }
        return ans;
    }
}

Time complexity: in the worst case, the statements in the while loop will be executed 2n times, for example, abcdefgg. At the beginning, j moves backward until it reaches the second g, and then i starts moving backward until n, so a total of 2n times are executed. The time complexity is O (n).

Spatial complexity: similar to the above, a Hash is required to save the substring, so it is O (min (m, n)). At this point, our solution has made do, but there are still places that can be optimized. Let's see solution 3

Step 3: solution 3

Continue to optimize, let's look at a case of the above algorithm.

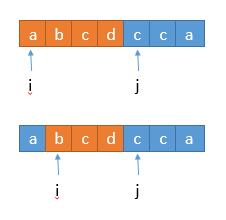
When the c pointed to by j exists in the preceding substring abcd, i moves forward to b. at this time, the substring still contains c and has to continue to move, so it can be optimized here. We can move directly to the next position of substring c in one step!

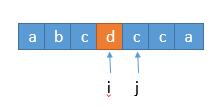
In this way, we will save the set as the subscript value in the map, and then we will implement it.

public class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length(), ans = 0;
        Map<Character, Integer> map = new HashMap<>(); 
        for (int j = 0, i = 0; j < n; j++) {
            if (map.containsKey(s.charAt(j))) {
                i = Math.max(map.get(s.charAt(j)), i); 
            }
            ans = Math.max(ans, j - i + 1);
            map.put(s.charAt(j), j + 1);//Subscript + 1 represents i the next position to move
        }
        return ans;
    }
}

Compared with solution II

Because it takes the form of i jump, the characters stored before map are not remove d, so math. Is performed in the if statement Max (map. Get (s.charat (J)), i). Make sure the subscript is not in front of i.

Another difference is that j adds 1 for each cycle, because the jump of i ensures that there is no duplicate string in str [i, j], so j can add 1 directly. In solution 2, we should keep the position of j unchanged, because we don't know where the character repeated with j is.

The last difference is that the ans is updated in each cycle. Because i was updated before the ans update, the current substring has been guaranteed to meet the conditions, so the ans can be updated. In solution 2, it is updated only when the current substring does not contain the current character.

Time complexity: we optimized 2n to N, but in the end, it is the same as before, O (n).

Spatial complexity: the same is true, O (min (m, n)).