In 1970, bloom filter was proposed to judge whether an element is not in a set, but it can not accurately determine whether the element is in the set.

Generally, to determine whether an element exists in the set of a business scenario, it is generally to save the element in the set and then determine it through comparison. For example, data structures such as linked list, tree and Hash Table (also known as Hash Table, Hash Table) are adopted. However, with the increase of elements in the collection, the required storage space will also show a linear growth, and finally reach the bottleneck. At the same time, the retrieval speed is becoming slower and slower. Therefore, in order to solve this time and space performance problem, bloom filter is introduced.

1. Data structure and principle

BloomFilter is composed of a fixed size binary vector or Bitmap and a series of mapping functions.

1.1 initialization

In the initial state, you need to specify the bitmap (array) length (N) and set all bits to 0.

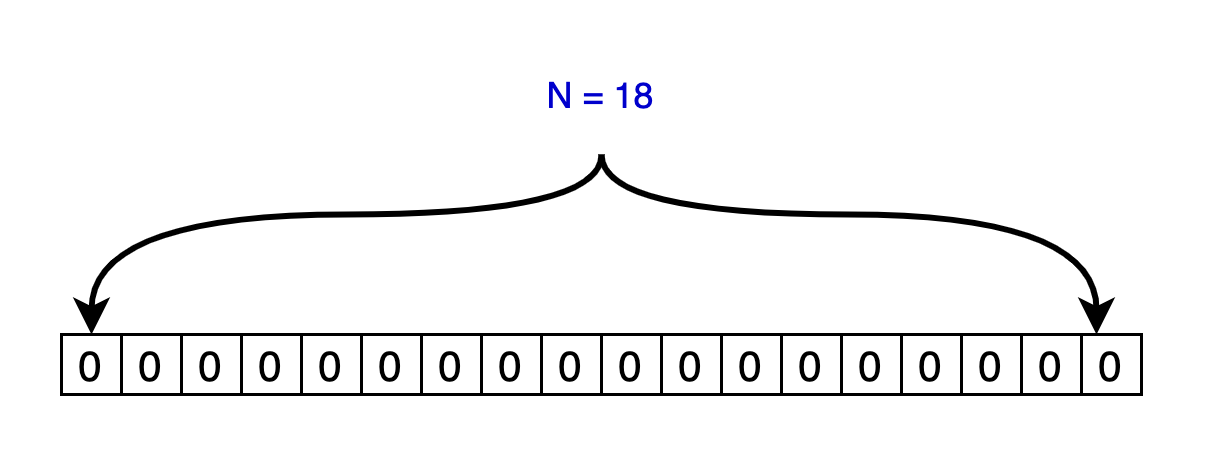
As shown in the figure above, assuming N=18, initialize array = 00 0000 0000.

1.2 variable mapping

The number of mapping times K needs to be specified for Bloom filter mapping, that is, the variable needs to be mapped to k points of the bitmap, and its position value is set to 1.

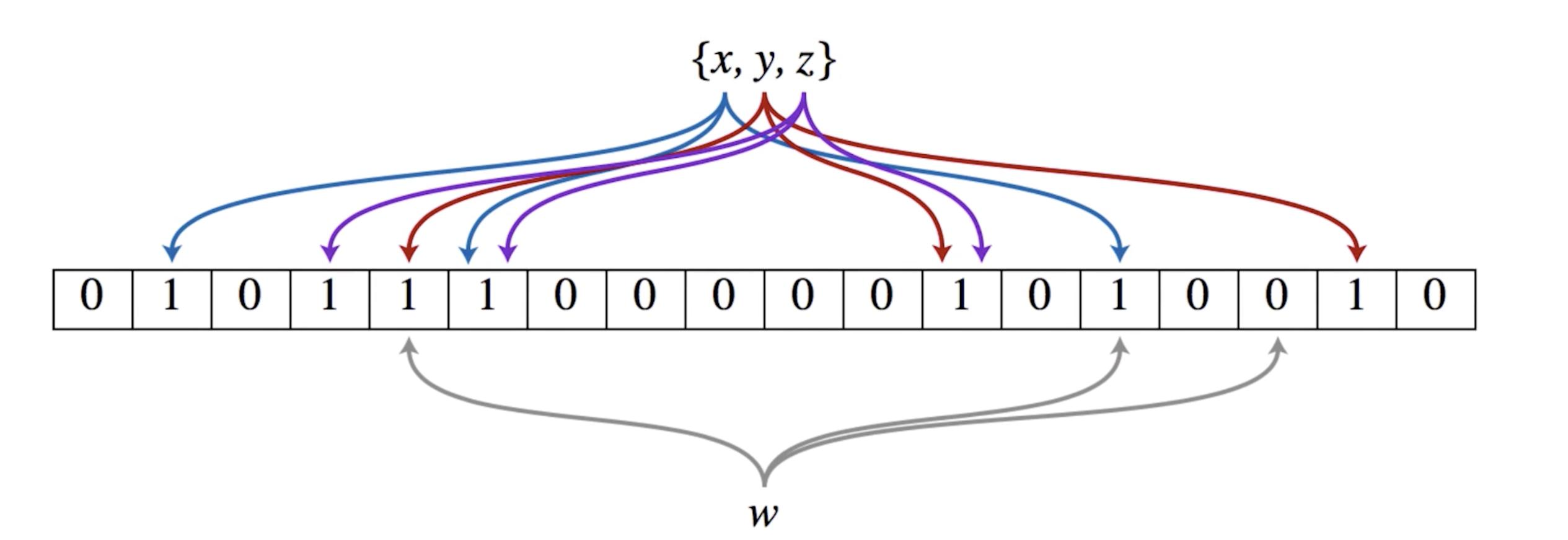
As shown in the figure above, assuming the bitmap length N=18 and the mapping times K=3, the hash calculation functions are hash1, hash2 and hash3 respectively.

Then, for element A={x, y, z}, add bloom filter, then:

element	First mapping position	Second mapping position	Third mapping position
x	hash1(x) % N = 1	hash2(x) % N = 5	hash3(x) % N = 13
y	hash1(y) % N = 4	hash2(y) % N = 11	hash3(y) % N = 16
z	hash1(z) % N = 3	hash2(z) % N = 5	hash3(z) % N = 11

Finally, the bloom filter string is 01 0111 0000 0101 0010

1.3 variable retrieval

At this time, the element w is added, and it needs to be judged whether it does not exist. Firstly, the position of the bloom filter is calculated through K-times mapping.

element	First mapping position	Second mapping position	Third mapping position
w	hash1(x) % N = 4	hash2(x) % N = 13	hash3(x) % N = 15

Secondly, read the value of the element where the mapping position is located. It can be found that the value of the third mapping position is 0, so it is determined that the element w does not exist in the filter.

1.4 summary

When retrieving a variable, you can roughly judge whether it exists in the set as long as you judge whether the mapping point values are all 1.

• If the mapping point has any 0, the retrieved variable must not exist;
• If they are all 1, the retrieved variable is likely to exist.

Thinking: why is it possible, not necessarily? That's because the mapping function itself is a hash function, and the hash function will collide.

2. Filter characteristics

2.1 misjudgment rate

Wrong judgment of Bloom filter: multiple keys are mapped and set to 1 in the same bit, so it is impossible to judge which input is generated. Therefore, the root of the wrong judgment is that the same bi bit is mapped and set to 1 for many times.

This situation also causes problems in deleting the bloom filter, because each bit of the bloom filter is not exclusive, and it is likely that multiple elements share a bit. If we delete this bit directly, it will affect other elements.

2.2 judgment characteristics

• If an element is judged to exist, the element does not necessarily exist, but it must not exist when it is judged not to exist.
• The bloom filter can add elements, but cannot delete elements. Because deleting elements will increase the misjudgment rate.

3. Case code

package org.apache.ithink;

/**
 * bloom filter
 * @author ithink/guojl.szu@hotmail.com
 * @date 2021-09-04
 */
public class BloomFilter {
  /**
   * Mapping times
   */
  private int k;
  /**
   * Bytes occupied by each Key
   */
  private int bitsPerKey;
  /**
   * Bitmap Size 
   */
  private int bitSize;
  /**
   * Underlying storage bitmap
   */
  private byte[] array;

  public BloomFilter(int k, int bitsPerKey) {
    this.k = k;
    this.bitsPerKey = bitsPerKey;
  }

  /**
   * Generate bitmap of key value
   * @param keys key
   * @return Key corresponding bitmap
   */
  public byte[] generate(String[] keys) {
    // Calculate the occupied digits of all keys
    int actualBitSize = keys.length * bitsPerKey;
    // Since each byte occupies 8 bits
    // bitSize + 7 / 8: avoid bitsize < 8, resulting in bitSize / 8 being 0
    // ((bitsize + 7) / 8) < < 3: ensure that the number of bits is an integer multiple of 8
    int middleBitSize = ((actualBitSize + 7) / 8) << 3; 
    // The Key occupies at least 64 bits
    int bitSize = middleBitSize < 64 ? 64 : middleBitSize;
    // Create a bitmap. Because byte is 8 bits, you need to divide all bits by 8
    array = new byte[bitSize >> 3];

	// Save bitmap footprint
	this.bitSize = bitSize;
    
    // Cyclic processing
    for (int i = 0; i < keys.length; i++) {
      // Generate Hash value
      int hashCode = Bytes.hash(keys[i].getBytes());
      // Cyclic mapping K times
      for (int t = 0; t < k; t++) {
        // Calculate the location of the bitmap
        // Hashcode% bitsize + bitsize: ensure that the modulus is not negative
        // (hashcode% bitSize + bitSize)% bitSize: there may be more than bitSize in parentheses, 
        //                                           Therefore, it is necessary to take the mold again for calculation
        int position = (hashCode % bitSize + bitSize) % bitSize;
        // Since each byte occupies 8 bits
        // Position% 8: which bit of the current byte is the calculation position
        // (1 < < (position% 8)): set the bit value of the byte to 1
        // position / 8: calculate the byte position of position
        array[position / 8] |= (1 << (position % 8));
        // Switch the first 17 bits and the last 15 bits of hashCode
        int delta = (hashCode >> 17) | (hashCode << 15);
        // Ensure that the hashCode of each calculation is different
        hashCode += delta;
      }
    }
    return array;
  }

  /**
   * Determine whether the Key exists
   * @param key key
   * @return true:Exists, false: does not exist
   */
  public boolean contains(String key) {
    // Generate hash value
    int hashCode = Bytes.hash(key.getBytes());
    // Cyclic mapping K times
    for (int t = 0; t < k; t++) {
      // Calculate the location of the bitmap
      int position = (hashCode % bitSize + bitSize) % bitSize;
      // If only one location value is 0, it means that it does not exist
      if ((array[position / 8] & (1 << (position % 8))) == 0) {
        return false;
      }
      // Switch the first 17 bits and the last 15 bits of hashCode
      int delta = (hashCode >> 17) | (hashCode << 15);
      hashCode += delta;
    }
    
    return true;
  }
}