1, Definition:
The idea of depth first search is very similar to the pre order traversal of the tree. The following is the definition on Baidu Encyclopedia:
The method of depth first traversing the graph is to start from a vertex v in the graph:
(1) Access vertex v;
(2) Starting from the unreachable adjacency points of v, the depth of the graph is traversed first; Until the vertices connected with v paths in the graph are accessed;
(3) If there are still vertices in the graph that have not been accessed at this time, start from an unreachable vertex and re traverse the depth first until all vertices in the graph have been accessed. Of course, when people have just mastered depth first search, they often use it to go through the maze In fact, we have another method, which is breadth first search (BFS)
The definition can be understood in combination with Fibonacci sequence (although it is a bad way to write Fibonacci with recursion), as shown in the following figure: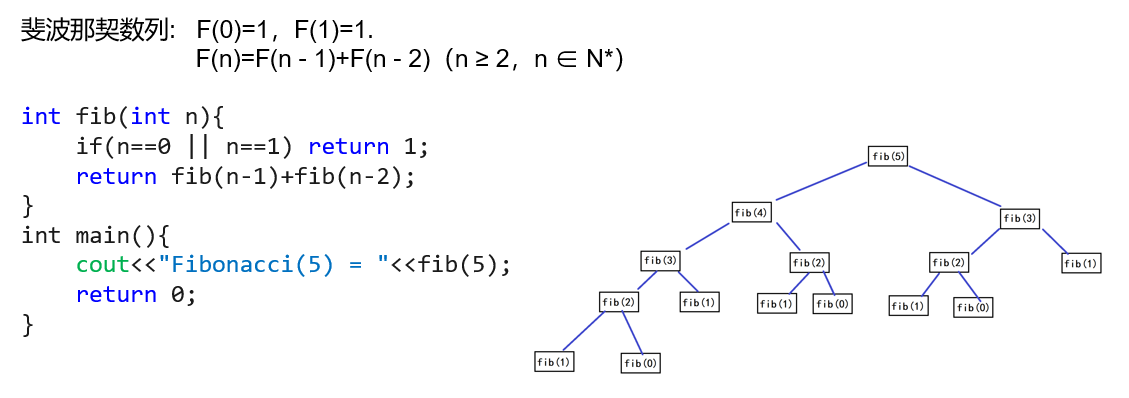
The order on the tree on the right is as follows:
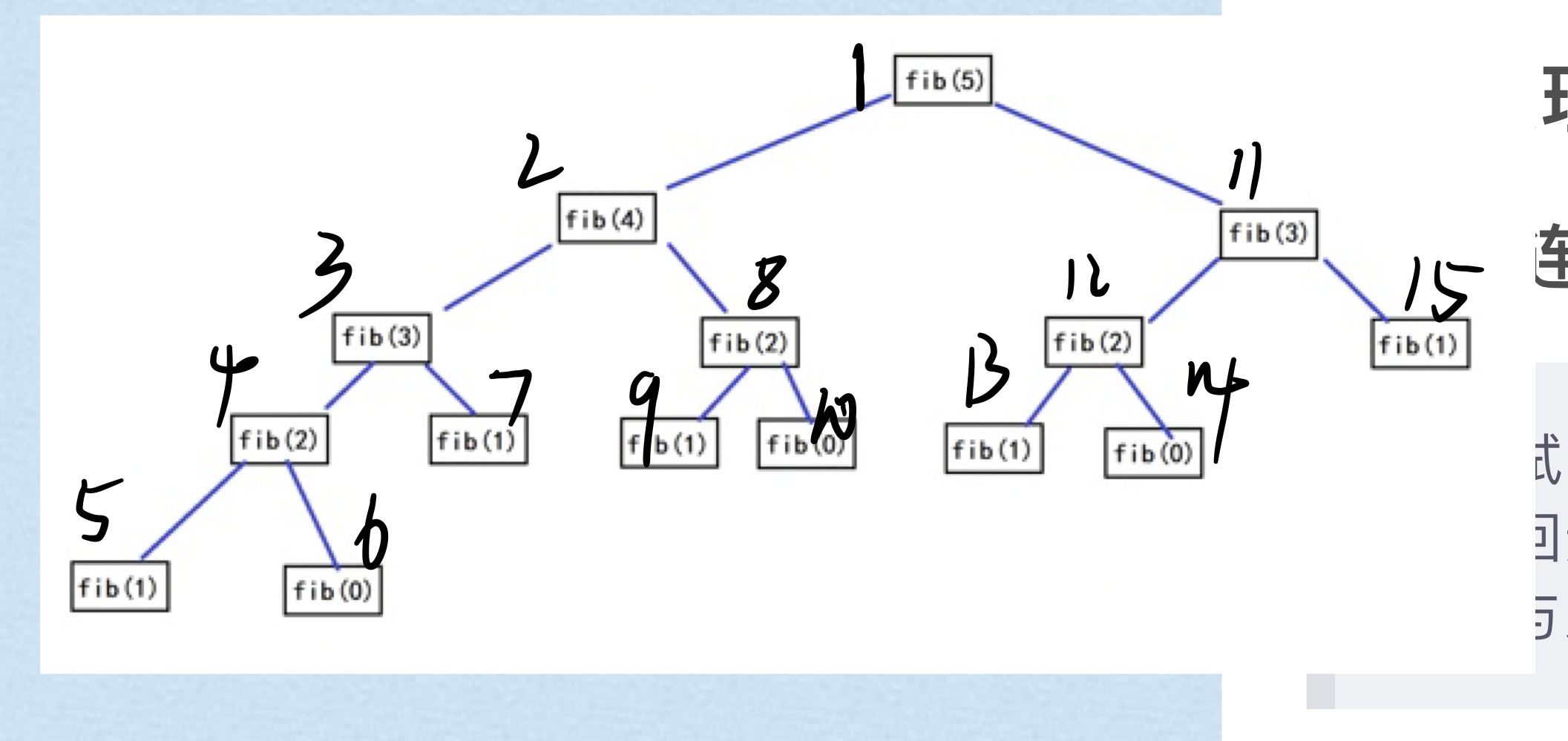
DFS can be understood in combination with the idea of traversal;
The topics of DFS can be roughly divided into two categories:
1. Check the connectivity of the graph: such as maze problem and conditional search of the graph.
2. DFS search order and rule questions. You can find the qualified solutions by exhausting all the answers. Instant search problem.
See here, you may have some doubts about the specific problem. This paper summarizes the principles of DFS and common question types, and attaches the code and problem-solving ideas.
2, Principle and analysis
1. DFS connectivity analysis:
In testing connectivity, the idea of DFS is consistent with people's thinking. On the same road, can I go on this road all the time? If I can't go on, I will return to the original node, change direction, and go on along the same road until I succeed.
For connectivity problems, we can also classify them:
1. No backtracking
In this problem, we only need to discard the searched nodes in each step, count the currently searched nodes, and finally count all the reachable points.
Here are two examples:
Example 1, Red and black (simple)
/*
* @Author: your name
* @Date: 2022-02-11 13:39:15
* @LastEditTime: 2022-02-11 13:56:51
* @LastEditors: Please set LastEditors
* @Description: Open koroFileHeader to view the configuration and set it: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE
* @FilePath: \All code\26.cpp
*/
#include<bits/stdc++.h>
using namespace std;
#define MAXN 100
char mp[MAXN][MAXN];
bool vis[MAXN][MAXN];
int W, H;
int ans;
int dx[4] = { 0, 1, 0, -1 };
int dy[4] = { 1, 0, -1, 0 };
void init()
{
for (int i = 0; i < MAXN; i++)
{
for (int j = 0; j < MAXN; j++)
{
vis[i][j] = false;
}
}
ans = 1;//Since it is at the initial point, it is a black brick at the beginning
}
void dfs(int x, int y)//Common DFS routines
{
for (int i = 0; i < 4; i++)
{
int newx = x + dx[i];
int newy = y + dy[i];
if (newx >= 1 && newx <= H && newy >= 1 && newy <= W && mp[newx][newy] == '.' && vis[newx][newy] == false)
{
ans++;
vis[newx][newy] = true;
dfs(newx, newy);
}
}
}
int beginx, beginy;
int main()
{
while (1)
{
cin >> W >> H;
if (W == 0 && H == 0)
{
break;
}
init();
for (int i = 1; i <= H; i++)
for (int j = 1; j <= W; j++)
{
cin >> mp[i][j];
if (mp[i][j] == '@')
{
beginx = i;
beginy = j;
}
}
dfs(beginx, beginy);
cout << ans << endl;
}
return 0;
}Example 2, Lake counting (simple staining method)
/*
* @Author: your name
* @Date: 2022-01-22 21:06:31
* @LastEditTime: 2022-01-22 21:32:59
* @LastEditors: Please set LastEditors
* @Description: Open koroFileHeader to view the configuration and set it: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE
* @FilePath: \All code\9.cpp
*/
#include <bits/stdc++.h>
using namespace std;
#define MAXN 105
bool vis[MAXN][MAXN];
char mp[MAXN][MAXN];
int row,cow;
int dx[8] = {0, 0, -1, 1, -1, -1, 1, 1};
int dy[8] = {-1, 1, 0, 0, -1, 1, -1, 1};
void dfs(int x,int y)
{
vis[x][y] = 1;
for(int i =0;i<8;i++)
{
int newx = x+dx[i];
int newy = y+dy[i];
if(newx>=0&&newy>=0&&newx<row&&newy<cow&&mp[newx][newy] == 'W'&&vis[newx][newy] ==0)
{
dfs(newx,newy);
}
}
}
int main()
{
int i, j;
int count =0;
cin >> row >> cow;
for (i = 0; i < row; i++)
for (j = 0; j < cow; j++)
{
cin >> mp[i][j];
}
for (i = 0; i < row; i++)
for (j = 0; j < cow; j++)
{
if(mp[i][j] == 'W'&&vis[i][j] == 0)//After encountering one, DFS is performed on the most important area and marked
{
dfs(i,j);
count++;
}
}
cout<<count;
return 0;
}With these two examples, I believe you begin to have a general understanding of DFS.
2, Need to backtrack: maze problems
As I mentioned in the introduction just now, if this path is different, you need to set up backtracking to restore the scene. The most classic is Maze problem (simple):
/*
* @Author: your name
* @Date: 2022-01-22 21:06:31
* @LastEditTime: 2022-01-22 22:12:20
* @LastEditors: Please set LastEditors
* @Description: Open fileHeader for configuration: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE
* @FilePath: \All code\9.cpp
*/
#include <bits/stdc++.h>
using namespace std;
#define MAXN 505
bool vis[MAXN][MAXN];
char mp[MAXN][MAXN];
int row, cow;
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
bool flag = false;
void dfs(int x, int y)
{
vis[x][y] = 1;
for (int i = 0; i < 4; i++)
{
int newx = x + dx[i];
int newy = y + dy[i];
if (newx >= 0 && newy >= 0 && newx < row && newy < cow && vis[newx][newy] == 0)
{
if (mp[newx][newy] == '.')
dfs(newx, newy);
if (mp[newx][newy] == 'E')
flag = true;
}
}
}
void init()
{
for (int i = 0; i < row; i++)
for (int j = 0; j < cow; j++)
{
vis[i][j] = 0;
}
}
int main()
{
int i, j;
int count = 0;
int row_s, cow_s;
while (cin >> row >> cow)
{
flag = false;
for (i = 0; i < row; i++)
for (j = 0; j < cow; j++)
{
cin >> mp[i][j];
if (mp[i][j] == 'S')
{
row_s = i;
cow_s = j;
}
}
init();
dfs(row_s, cow_s);
if (flag == true)
{
cout << "Yes" << endl;
}
else
{
cout << "No" << endl;
}
}
return 0;
}In addition, there is an example for counting: Ma Zori
This question only changes the path selection and success conditions of the maze problem. It is also a simple search problem:
/*
* @Author: your name
* @Date: 2022-02-11 14:44:55
* @LastEditTime: 2022-02-11 15:30:56
* @LastEditors: Please set LastEditors
* @Description: Open koroFileHeader to view the configuration and set it: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE
* @FilePath: \All code\28.cpp
*/
#include <iostream>
using namespace std;
#define MAXN 15
int mp[MAXN][MAXN];
bool vis[MAXN][MAXN];
int row, cow, newx, newy;
int ans;
int dx[8] = { -2, -2, 2, 2, -1, -1, 1, 1 };
int dy[8] = { 1, -1, 1, -1, -2, 2, -2, 2 };
void init()
{
for (int i = 0; i < MAXN; i++)
{
for (int j = 0; j < MAXN; j++)
{
vis[i][j] = false;
}
}
ans = 0;
}
void dfs(int x, int y, int depth)
{
for (int i = 0; i < 8; i++)
{
int newx = x + dx[i];
int newy = y + dy[i];
if (newx >= 1 && newx <= row && newy >= 1 && newy <= cow && vis[newx][newy] == false)
{
vis[newx][newy] = true;
if (depth == row * cow - 1)//Since this is newx, it has not been recursive to a new layer, so it needs to be reduced by 1
{
ans++;
}
dfs(newx, newy, depth + 1);
vis[newx][newy] = false;
}
}
}
int main()
{
int T;
cin >> T;
while (T--)
{
cin >> row >> cow >> newx >> newy;
init();
vis[newx + 1][newy + 1] = true;
dfs(newx + 1, newy + 1, 1);//It should be noted here that when I started from the first step, I was already on the first floor, not on the 0 th floor.
cout << ans << endl;
}
return 0;
}When I started this problem, I made such a mistake: I read the layers of the deadline wrong. We should pay attention to this problem when writing code.
Summarize the DFS template
Function DFS (current state){
If (current status = = destination status){
···
}
for(·····················){
If (legal status){
vis [access this point];
DFS (new status);
? Need to restore site - > vis [restore access]
}
}
If (new status not found){
···
}
}
2. Solve problems exhaustively
Example: part and question:

#include <bits/stdc++.h>
using namespace std;
int n, k;
int a[35];
bool dfs(int id, int sum)
{
if (sum == k)
return 1;
if (id > n)
return 0;
if (1 == dfs(id + 1, sum + a[id]))
return 1;
if (1 == dfs(id + 1, sum))
return 1;
return 0;
}
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
if (1 == dfs(1, 0))
{
puts("YES");
}
else
{
puts("NO");
}
return 0;
}
It's also very simple. Just discuss whether the current number is selected in each step once. For this problem, if you want to find the least number of sequences added as k, you can also use the exhaustive method to write. At the same time, we can also use the knowledge of dynamic programming to solve problems. Readers can go down and think for themselves.