ResNet, a deep residual network, won the Best Paper Award at the 2016 CVPR conference and has so far received 38295 academic citations from Google.
The deep residual shrinking network is a new and improved version of deep residual network, which is actually a deep integration of deep residual network, attention mechanism and soft threshold function.
To some extent, the working principle of the deep residual shrinking network can be understood as: noticing unimportant features through the attention mechanism and setting them to zero through the soft threshold function; or noticing important features through the attention mechanism and preserving them, thereby strengthening the ability of the deep residual shrinking network to extract useful features from noisy signals.
1. What is the motivation for proposing a deep residual shrinking network?
First, when classifying samples, there will inevitably be some noise in the samples, such as Gaussian noise, pink noise, Laplace noise, etc.More broadly, samples may contain information that is irrelevant to the current classification task and can also be interpreted as noise.These noises may adversely affect the classification results.(Soft thresholding is a key step in many signal denoising algorithms)
For example, when you are chatting along the street, the sounds of chatting may be mixed with the sounds of cars'whistles, wheels, and so on.When these sound signals are recognized by speech recognition, the recognition effect will inevitably be affected by the sound of whistle and wheel.From the perspective of in-depth learning, the corresponding features of these whistles and wheel sounds should be deleted from the deep neural network to avoid affecting the effect of speech recognition.
Secondly, even for the same sample set, the noise level of each sample is often different.(This has something in common with the attention mechanism; for example, with a sample set of images, the location of the target object may be different in each picture; the attention mechanism can focus on the location of the target object for each picture)
For example, when training a cat and dog classifier, for five images labeled "dog", the first image may contain both dog and mouse, the second image may contain both dog and goose, the third image may contain both dog and chicken, the fourth image may contain both dog and donkey, and the fifth image may contain both dog and duck.When we train the cat and dog classifier, we will inevitably be disturbed by unrelated objects such as rats, geese, chickens, donkeys and ducks, which will cause the classification accuracy to decrease.If we can notice these unrelated mice, geese, chickens, donkeys and ducks and remove their corresponding features, it is possible to improve the accuracy of cat and dog classifiers.
2. Soft thresholding is the core step of many noise reduction algorithms
Soft thresholding is the core step of many signal denoising algorithms. It deletes the features whose absolute values are less than a certain threshold and shrinks the features whose absolute values are greater than this threshold toward zero.It can be achieved by the following formula:
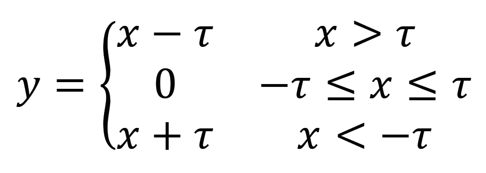
Soft Threshold Output Derivative to Input
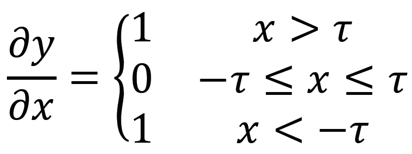
As you can see from this, the derivative of soft thresholding is either 1 or 0.This property is the same as the ReLU activation function.Therefore, soft thresholding can also reduce the risk of gradient dispersion and gradient explosion for deep learning algorithms.
In the soft thresholding function, the setting of threshold must satisfy two conditions: first, the threshold is positive; second, the threshold cannot be greater than the maximum of the input signal, otherwise the output will be all zero.
At the same time, a third condition is best met: each sample should have its own independent threshold according to its own noise level.
This is because the noise content of many samples is often different.This is often the case, for example, where sample A contains less noise and sample B contains more noise in the same sample set.Then, if soft thresholding is used in the noise reduction algorithm, Sample A should use a larger threshold and Sample B should use a smaller threshold.In deep neural networks, although these features and thresholds lose clear physical meaning, the basic principles are common.That is, each sample should have its own independent threshold according to its own noise level.
3. Attention mechanism
Attention mechanisms are easy to understand in the field of computer vision.The animal's visual system can quickly scan all areas to discover the target object, thereby focusing attention on the target object to extract more details while suppressing extraneous information.Refer specifically to the article on attention mechanisms.
Squeeze-and-Excitation Network (SENet) is a more recent method of in-depth learning with a focus mechanism.In different samples, different feature channels often contribute different sizes to classification tasks.SENet uses a small subnetwork to obtain a set of weights, which are then multiplied by the characteristics of each channel to adjust the size of each channel feature.This process can be thought of as exerting different sizes of attention on each characteristic channel.
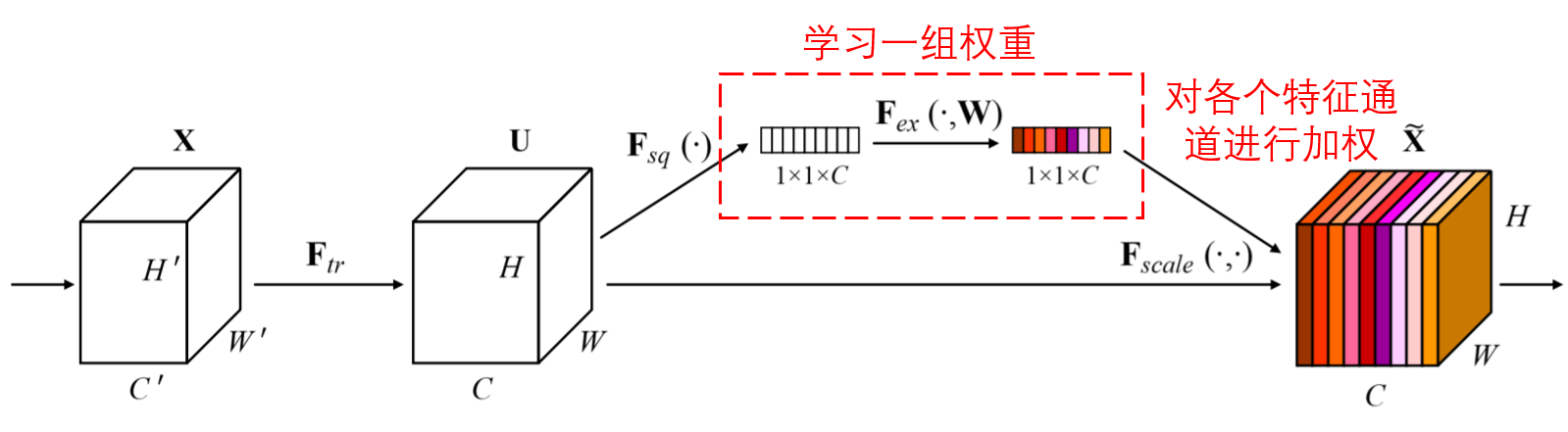
In this way, each sample will have its own independent set of weights.In other words, any two samples have different weights.In SENet, the specific path to get the weight is "global pooling_full connection layer_ReLU function_full connection layer_Sigmoid function".
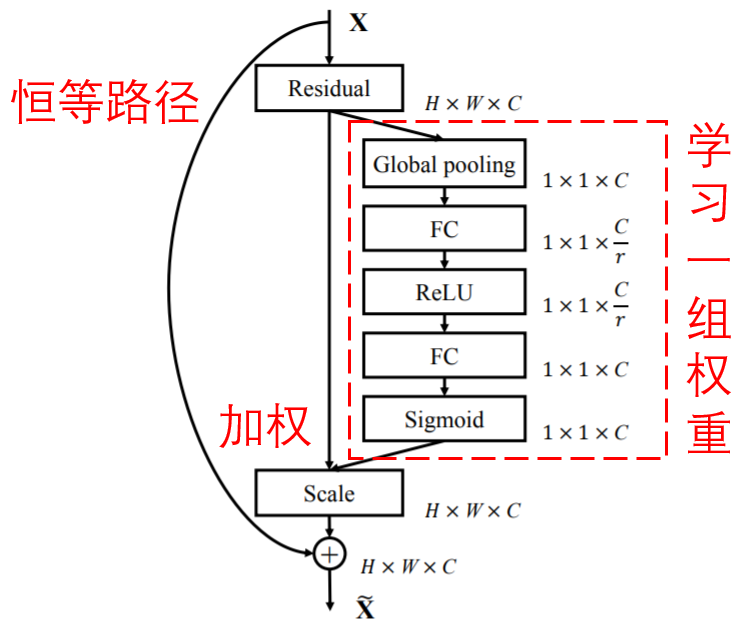
4. Soft thresholding under deep attention mechanism
The deep residual shrinking network refers to the subnetwork structure of SENet above to achieve soft thresholding under the attention mechanism.By subnets in the blue box, you can learn to get a set of thresholds to soften each feature channel.
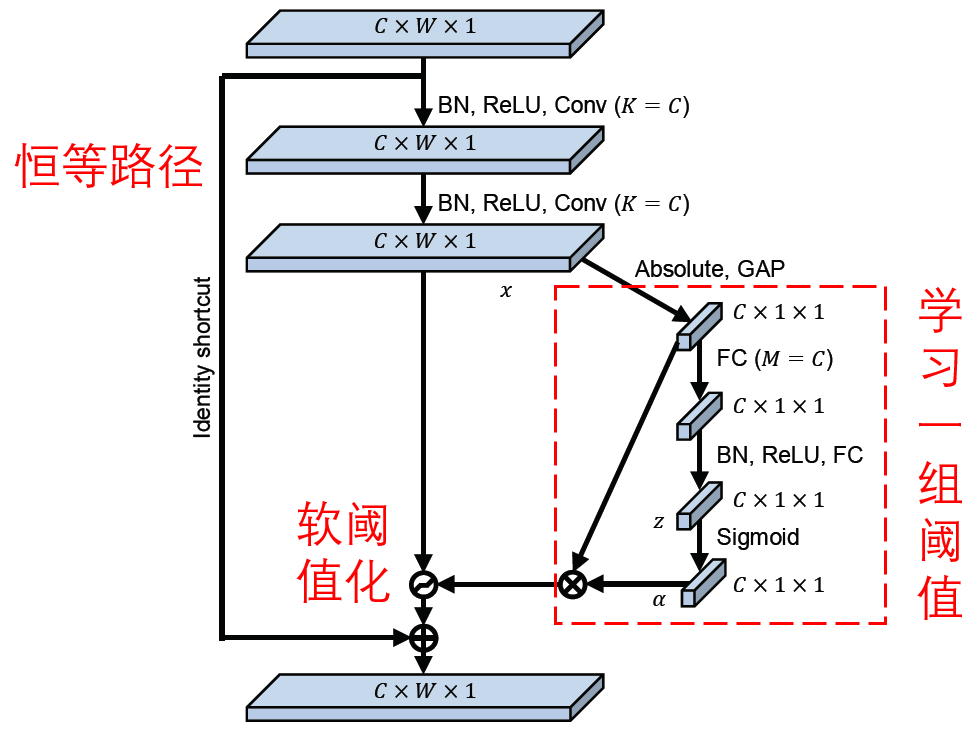
In this subnetwork, the absolute values of all the features of the input signature graph are first obtained.After global mean pooling and averaging, a feature is obtained, which is denoted as A.In another path, the global mean pooled signature graph is input to a small, fully connected network.This fully connected network takes the Sigmoid function as its last layer, normalizes the output between 0 and 1, and obtains a coefficient, which is denoted as alpha.The final threshold can be expressed as alpha*A.Therefore, the threshold is the average of the absolute values of a digital x-signature graph between 0 and 1.In this way, the threshold is positive and not too large.
Furthermore, different samples have different thresholds.Therefore, to a certain extent, it can be understood as a special attention mechanism: noting features that are not relevant to the current task, setting them to zero by soft thresholding, or noticing features that are relevant to the current task and preserving them.
Finally, a complete deep residual shrinking network is obtained by stacking a number of basic modules as well as convolution layers, batch standardization, activation functions, global mean pooling, and fully connected output layers.
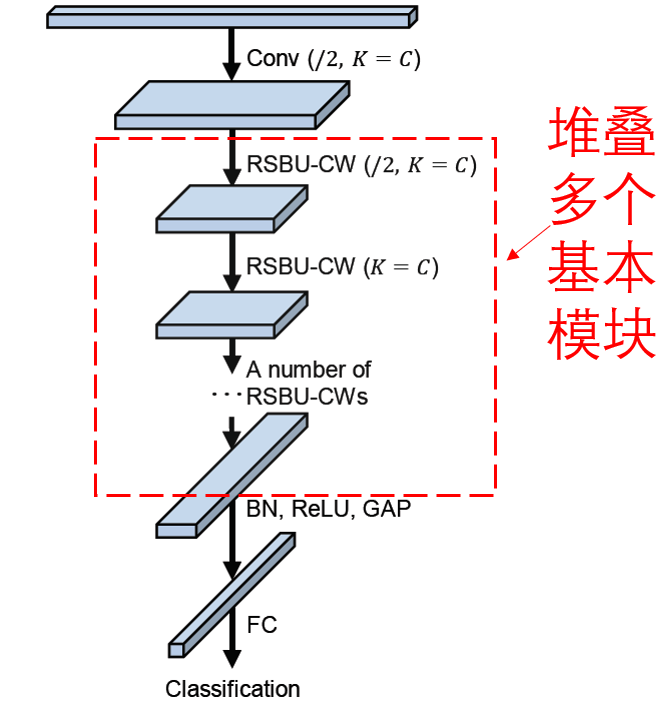
5. Deep residual shrinking networks may have wider generality
The deep residual shrinking network is actually a general feature learning method.This is because many feature learning tasks involve more or less noise and unrelated information in the samples.These noises and irrelevant information may affect the effect of feature learning.For example:
When classifying pictures, these objects can be interpreted as "noise" if the pictures contain many other objects at the same time; the deep residual shrinking network may be able to use the attention mechanism to notice these "noise" and then use soft thresholding to set the corresponding features of these "noise" to zero, which may improve the accuracy of image classification.
In speech recognition, if you are chatting in noisy environments, such as roadside or factory workshops, the deep residual shrinking network may improve the accuracy of speech recognition, or provide a way of thinking to improve the accuracy of speech recognition.
6. Introduction to Keras and TFLearn programs
This program takes image classification as an example, builds a small depth residual shrinking network, and the superparameters are not optimized.In order to achieve high accuracy, you can increase the depth, increase the number of training iterations, and adjust the superparameters appropriately.Here is the Keras program:
#!/usr/bin/env python3 # -*- coding: utf-8 -*- """ Created on Sat Dec 28 23:24:05 2019 Implemented using TensorFlow 1.0.1 and Keras 2.2.1 M. Zhao, S. Zhong, X. Fu, et al., Deep Residual Shrinkage Networks for Fault Diagnosis, IEEE Transactions on Industrial Informatics, 2019, DOI: 10.1109/TII.2019.2943898 @author: super_9527 """ from __future__ import print_function import keras import numpy as np from keras.datasets import mnist from keras.layers import Dense, Conv2D, BatchNormalization, Activation from keras.layers import AveragePooling2D, Input, GlobalAveragePooling2D from keras.optimizers import Adam from keras.regularizers import l2 from keras import backend as K from keras.models import Model from keras.layers.core import Lambda K.set_learning_phase(1) # Input image dimensions img_rows, img_cols = 28, 28 # The data, split between train and test sets (x_train, y_train), (x_test, y_test) = mnist.load_data() if K.image_data_format() == 'channels_first': x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols) x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols) input_shape = (1, img_rows, img_cols) else: x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1) x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1) input_shape = (img_rows, img_cols, 1) # Noised data x_train = x_train.astype('float32') / 255. + 0.5*np.random.random([x_train.shape[0], img_rows, img_cols, 1]) x_test = x_test.astype('float32') / 255. + 0.5*np.random.random([x_test.shape[0], img_rows, img_cols, 1]) print('x_train shape:', x_train.shape) print(x_train.shape[0], 'train samples') print(x_test.shape[0], 'test samples') # convert class vectors to binary class matrices y_train = keras.utils.to_categorical(y_train, 10) y_test = keras.utils.to_categorical(y_test, 10) def abs_backend(inputs): return K.abs(inputs) def expand_dim_backend(inputs): return K.expand_dims(K.expand_dims(inputs,1),1) def sign_backend(inputs): return K.sign(inputs) def pad_backend(inputs, in_channels, out_channels): pad_dim = (out_channels - in_channels)//2 return K.spatial_3d_padding(inputs, padding = ((0,0),(0,0),(pad_dim,pad_dim))) # Residual Shrinakge Block def residual_shrinkage_block(incoming, nb_blocks, out_channels, downsample=False, downsample_strides=2): residual = incoming in_channels = incoming.get_shape().as_list()[-1] for i in range(nb_blocks): identity = residual if not downsample: downsample_strides = 1 residual = BatchNormalization()(residual) residual = Activation('relu')(residual) residual = Conv2D(out_channels, 3, strides=(downsample_strides, downsample_strides), padding='same', kernel_initializer='he_normal', kernel_regularizer=l2(1e-4))(residual) residual = BatchNormalization()(residual) residual = Activation('relu')(residual) residual = Conv2D(out_channels, 3, padding='same', kernel_initializer='he_normal', kernel_regularizer=l2(1e-4))(residual) # Calculate global means residual_abs = Lambda(abs_backend)(residual) abs_mean = GlobalAveragePooling2D()(residual_abs) # Calculate scaling coefficients scales = Dense(out_channels, activation=None, kernel_initializer='he_normal', kernel_regularizer=l2(1e-4))(abs_mean) scales = BatchNormalization()(scales) scales = Activation('relu')(scales) scales = Dense(out_channels, activation='sigmoid', kernel_regularizer=l2(1e-4))(scales) scales = Lambda(expand_dim_backend)(scales) # Calculate thresholds thres = keras.layers.multiply([abs_mean, scales]) # Soft thresholding sub = keras.layers.subtract([residual_abs, thres]) zeros = keras.layers.subtract([sub, sub]) n_sub = keras.layers.maximum([sub, zeros]) residual = keras.layers.multiply([Lambda(sign_backend)(residual), n_sub]) # Downsampling (it is important to use the pooL-size of (1, 1)) if downsample_strides > 1: identity = AveragePooling2D(pool_size=(1,1), strides=(2,2))(identity) # Zero_padding to match channels (it is important to use zero padding rather than 1by1 convolution) if in_channels != out_channels: identity = Lambda(pad_backend)(identity, in_channels, out_channels) residual = keras.layers.add([residual, identity]) return residual # define and train a model inputs = Input(shape=input_shape) net = Conv2D(8, 3, padding='same', kernel_initializer='he_normal', kernel_regularizer=l2(1e-4))(inputs) net = residual_shrinkage_block(net, 1, 8, downsample=True) net = BatchNormalization()(net) net = Activation('relu')(net) net = GlobalAveragePooling2D()(net) outputs = Dense(10, activation='softmax', kernel_initializer='he_normal', kernel_regularizer=l2(1e-4))(net) model = Model(inputs=inputs, outputs=outputs) model.compile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy']) model.fit(x_train, y_train, batch_size=100, epochs=5, verbose=1, validation_data=(x_test, y_test)) # get results K.set_learning_phase(0) DRSN_train_score = model.evaluate(x_train, y_train, batch_size=100, verbose=0) print('Train loss:', DRSN_train_score[0]) print('Train accuracy:', DRSN_train_score[1]) DRSN_test_score = model.evaluate(x_test, y_test, batch_size=100, verbose=0) print('Test loss:', DRSN_test_score[0]) print('Test accuracy:', DRSN_test_score[1])
Here is the TFLearn program:
#!/usr/bin/env python3 # -*- coding: utf-8 -*- """ Created on Mon Dec 23 21:23:09 2019 Implemented using TensorFlow 1.0 and TFLearn 0.3.2 M. Zhao, S. Zhong, X. Fu, B. Tang, M. Pecht, Deep Residual Shrinkage Networks for Fault Diagnosis, IEEE Transactions on Industrial Informatics, 2019, DOI: 10.1109/TII.2019.2943898 @author: super_9527 """ from __future__ import division, print_function, absolute_import import tflearn import numpy as np import tensorflow as tf from tflearn.layers.conv import conv_2d # Data loading from tflearn.datasets import cifar10 (X, Y), (testX, testY) = cifar10.load_data() # Add noise X = X + np.random.random((50000, 32, 32, 3))*0.1 testX = testX + np.random.random((10000, 32, 32, 3))*0.1 # Transform labels to one-hot format Y = tflearn.data_utils.to_categorical(Y,10) testY = tflearn.data_utils.to_categorical(testY,10) def residual_shrinkage_block(incoming, nb_blocks, out_channels, downsample=False, downsample_strides=2, activation='relu', batch_norm=True, bias=True, weights_init='variance_scaling', bias_init='zeros', regularizer='L2', weight_decay=0.0001, trainable=True, restore=True, reuse=False, scope=None, name="ResidualBlock"): # residual shrinkage blocks with channel-wise thresholds residual = incoming in_channels = incoming.get_shape().as_list()[-1] # Variable Scope fix for older TF try: vscope = tf.variable_scope(scope, default_name=name, values=[incoming], reuse=reuse) except Exception: vscope = tf.variable_op_scope([incoming], scope, name, reuse=reuse) with vscope as scope: name = scope.name #TODO for i in range(nb_blocks): identity = residual if not downsample: downsample_strides = 1 if batch_norm: residual = tflearn.batch_normalization(residual) residual = tflearn.activation(residual, activation) residual = conv_2d(residual, out_channels, 3, downsample_strides, 'same', 'linear', bias, weights_init, bias_init, regularizer, weight_decay, trainable, restore) if batch_norm: residual = tflearn.batch_normalization(residual) residual = tflearn.activation(residual, activation) residual = conv_2d(residual, out_channels, 3, 1, 'same', 'linear', bias, weights_init, bias_init, regularizer, weight_decay, trainable, restore) # get thresholds and apply thresholding abs_mean = tf.reduce_mean(tf.reduce_mean(tf.abs(residual),axis=2,keep_dims=True),axis=1,keep_dims=True) scales = tflearn.fully_connected(abs_mean, out_channels//4, activation='linear',regularizer='L2',weight_decay=0.0001,weights_init='variance_scaling') scales = tflearn.batch_normalization(scales) scales = tflearn.activation(scales, 'relu') scales = tflearn.fully_connected(scales, out_channels, activation='linear',regularizer='L2',weight_decay=0.0001,weights_init='variance_scaling') scales = tf.expand_dims(tf.expand_dims(scales,axis=1),axis=1) thres = tf.multiply(abs_mean,tflearn.activations.sigmoid(scales)) # soft thresholding residual = tf.multiply(tf.sign(residual), tf.maximum(tf.abs(residual)-thres,0)) # Downsampling if downsample_strides > 1: identity = tflearn.avg_pool_2d(identity, 1, downsample_strides) # Projection to new dimension if in_channels != out_channels: if (out_channels - in_channels) % 2 == 0: ch = (out_channels - in_channels)//2 identity = tf.pad(identity, [[0, 0], [0, 0], [0, 0], [ch, ch]]) else: ch = (out_channels - in_channels)//2 identity = tf.pad(identity, [[0, 0], [0, 0], [0, 0], [ch, ch+1]]) in_channels = out_channels residual = residual + identity return residual # Real-time data preprocessing img_prep = tflearn.ImagePreprocessing() img_prep.add_featurewise_zero_center(per_channel=True) # Real-time data augmentation img_aug = tflearn.ImageAugmentation() img_aug.add_random_flip_leftright() img_aug.add_random_crop([32, 32], padding=4) # Build a Deep Residual Shrinkage Network with 3 blocks net = tflearn.input_data(shape=[None, 32, 32, 3], data_preprocessing=img_prep, data_augmentation=img_aug) net = tflearn.conv_2d(net, 16, 3, regularizer='L2', weight_decay=0.0001) net = residual_shrinkage_block(net, 1, 16) net = residual_shrinkage_block(net, 1, 32, downsample=True) net = residual_shrinkage_block(net, 1, 32, downsample=True) net = tflearn.batch_normalization(net) net = tflearn.activation(net, 'relu') net = tflearn.global_avg_pool(net) # Regression net = tflearn.fully_connected(net, 10, activation='softmax') mom = tflearn.Momentum(0.1, lr_decay=0.1, decay_step=20000, staircase=True) net = tflearn.regression(net, optimizer=mom, loss='categorical_crossentropy') # Training model = tflearn.DNN(net, checkpoint_path='model_cifar10', max_checkpoints=10, tensorboard_verbose=0, clip_gradients=0.) model.fit(X, Y, n_epoch=100, snapshot_epoch=False, snapshot_step=500, show_metric=True, batch_size=100, shuffle=True, run_id='model_cifar10') training_acc = model.evaluate(X, Y)[0] validation_acc = model.evaluate(testX, testY)[0]
Paper Web Site
M. Zhao, S. Zhong, X. Fu, et al., Deep residual shrinkage networks for fault diagnosis, IEEE Transactions on Industrial Informatics, DOI: 10.1109/TII.2019.2943898