data structure

Main contents:
Introduction to data structure
linear structure
tree structure

Introduction to data structure

1 what is a data structure

In short, a data structure is a container that stores data in a specific layout. This "layout" determines that a data structure is efficient for some operations and inefficient for others Therefore, we need to understand various data structures in order to select the most appropriate data structure when dealing with practical problems.

Data structure = logical structure + physical structure (sequence, chain, index, hash)
Logical structure: abstract relationship between data elements
Physical structure: (storage structure), the form of storage in computer memory

2 logical classification of data structure

Data structures are logically divided into three basic types:

2.1 linear structure

There is a one-to-one relationship between the elements in the data structure;
Common linear structures:
Linear table, stack, queue, string (one-dimensional array), etc.

2.2 tree structure

There is a one to many relationship between the elements in the data structure;
Common tree structure:
Binary tree, red black tree, B tree, Huffman tree, etc.

2.3 graphic structure

The elements in the data structure have many to many relationships;
Common graphic structures:
Directed graph, undirected graph, simple graph, etc.

2, Linear structure

1 stack structure

1.1 definition of stack

Stack is a storage structure that can only access data from one end and follows the "last in first out (LIFO)" principle.

1.2 implementation of stack container

1.2.1 create stack container

/**
* Custom stack container
*/
public class MyStack<E> {
	private Object[] arr;//Physical structure of storage elements
	private int stackLength = 4;//Default length of array
	private int size; //Record the number of elements in the stack container
	private int index = -1;//Pointer to the subscript position of the operation array
	/**
	* Determine whether the stack container is empty
	* @return
	*/
	public boolean empty(){
		return false;
	}
	/**
	* Get stack top element
	* @return
	*/
	public E pop(){
		return null;
	}
	/**
	* Add element to stack container
	* @param item
	* @return
	*/
	public E push(E item){
		return null;
	}
	public static void main(String[] args) {
	}
}

1.2.2 implementation of adding elements

 /**
     * Add element to stack container
     * @param item
     * @return
     */
    public E push(E item){
        //Initialize array
        this.capacity();
        //Adding elements to an array
        this.arr[++index]=item;
        //Number of record elements
        this.size++;
        return item;
    }

    /**
     * Initialize the array or expand the capacity of the array by 1.5 times the capacity
     */
    private void capacity(){
        //Data initialization
        if(this.arr == null){
            this.arr = new Object[this.stackLength];
        }
        //Expand the array by 1.5x
        if(this.size - (this.stackLength-1) >= 0){
            this.stackLength = this.stackLength + (this.stackLength >> 1);
            this.arr = Arrays.copyOf(this.arr,this.stackLength);
        }
    }

1.2.3 implementation acquisition element

/**
* Get stack top element
* @return
*/
public E pop(){
	//Throw an exception if there are no elements in the stack container
	if(this.index == -1){
	throw new EmptyStackException();
	}
	//Number of record elements
	this.size--;
	//Return stack top element
	return (E) this.arr[index--];
}

1.2.4 judge whether the stack container is empty

/**
* Determine whether the stack container is empty
* @return
*/
public boolean empty(){
	return this.size == 0;
}

2 linked list structure

2.1 definition of linked list structure

2.1.1 what is a linked list

The linked list structure is composed of many nodes, and each node contains two parts:

• Data part: save the actual data of this node.
• Address part: saves the address of the previous or next node.

2.1.2 linked list classification

• Unidirectional linked list
• Bidirectional linked list
• Bidirectional circular linked list

2.1.3 characteristics of linked list

• The location of nodes in memory is arbitrary, that is, logically adjacent data elements are not necessarily adjacent physically.
• When accessing, you can only enter the linked list through the head or tail pointer, and scan the other nodes backward or forward through the pointer field of each node, so the time spent looking for the first node and the last node is different.

Advantages and disadvantages of linked list:

• Advantages: the number of data elements can be expanded, inserted, deleted and other operations freely. There is no need to move the data, just modify the link pointer, and the modification efficiency is high.
• Disadvantages: sequential access must be adopted, that is, when accessing data elements, they can only be accessed in the order of linked list, and the efficiency of access nodes is low.

2.2 one way linked list structure

2.2.1 definition of one-way linked list

One way linked list (single linked list) is a kind of linked list. Its characteristic is that the link direction of the linked list is one-way. The access to the linked list should be read sequentially from the head.

2.2.2 realize one-way linked list

2.2.2.1 create linked list interface

/**
* Method API definition of accessing elements based on linked list structure
* @param <E>
*/
public interface MyList<E> {
	void add(E element);
	E get(int index);
	int size();
	E remove(int index);
}

2.2.2.2 create a one-way linked list class

/**
* Container for element access based on one-way linked list
* @param <E>
*/
public class MySinglyLinkedList<E> implements MyList<E> {
	/**
	* Add elements to the linked list
	* @param element
	*/
	@Override
	public void add(E element) {
	}
	/**
	* Get elements based on their location
	* @param index
	* @return
	*/
	@Override
	public E get(int index) {
		return null;
	}
	/**
	* Get the number of elements
	* @return
	*/
	@Override
	public int size() {
		return 0;
	}
	/**
	* Delete elements based on their location
	* @param index
	* @return
	*/
	@Override
	public E remove(int index) {
		return null;
	}
	public static void main(String[] args) {
	}
}

2.2.2.3 create node class

/**
* Define node objects in a one-way linked list
*/
class Node<E>{
	private E item;//Storage element
	private Node next;//Stores the address of the next node object
	Node(E item,Node next){
		this.item = item;
		this.next = next;
	}
}

2.2.2.4 method of adding elements

private Node head;//Store the header node in the linked list.
private int size;//Record the number of elements.
	/**
	* Add elements to the linked list
	* @param element
	*/
	@Override
	public void add(E element) {
		//Create node
		Node<E> node = new Node<>(element,null);
		//Find tail node
		Node tail = getTail();
		//Hooking of nodes
		if(tail == null)
			this.head = node;
		else
			tail.next = node;
		//Number of record elements
		this.size++;
	}
	/**
	* Tail finding node
	*/
	private Node getTail(){
		//Whether the header node exists
		if(this.head == null){
			return null;
	}
	//Find tail node
	Node node = this.head;
	while(true){
		if(node.next == null)break;
		node = node.next;//Move the pointer to the next node
	}
	return node;
}

2.2.2.5 method of obtaining elements

/**
* Get elements based on their location
* @param index
* @return
*/
@Override
public E get(int index) {
		//Verify the validity of Index
		this.checkIndex(index);
		//Get the specified node according to the location
		Node<E> node = this.getNode(index);
		//Returns the elements in this node
		return node.item;
	}
	/**
	* Verify the Index
	*/
	private void checkIndex(int index){
		if(!(index >= 0 && index < this.size)){
			throw new IndexOutOfBoundsException("Index: "+index+" Size:"+this.size);
		}
	}
	/**
	* Get nodes based on location
	*/
	private Node getNode(int index){
		Node<E> node = this.head;
		for(int i=0;i<index;i++){
			node = node.next;
		}
	return node;
}

2.2.2.6 implement the method of deleting elements

/**
* Delete elements based on their location
* @param index
* @return
*/
@Override
public E remove(int index) {
	//Verify the validity of Index
	this.checkIndex(index);
	//Locate the node object by location
	Node<E> node = this.getNode(index);
	//Gets the element in the node object
	E item = node.item;
	//Remove the node object from the one-way linked list
	//Judge whether the currently deleted node is a header node
	if(this.head == node){
		this.head = node.next;
	}else{
		Node<E> temp = this.head;
		for(int i=0;i< index - 1;i++){
			temp = temp.next;
		}
		temp.next = node.next;
	}
	node.next = null;
	//Number of record elements
	this.size--;
	//Return the element to
	return item;
}

2.2.2.7 get the number of elements

/**
* Get the number of elements
* @return
*/
@Override
public int size() {
	return this.size;
}

2.3 two way linked list structure

2.3.1 definition of bidirectional linked list

Bidirectional linked list, also known as double linked list, is a kind of linked list. There are two pointers in each data node, pointing to the direct precursor and direct successor respectively.

2.3.2 realize bidirectional linked list

2.3.2.1 create a two-way linked list class

/**
* Container for element access based on bidirectional linked list
* @param <E>
*/
public class MyDoublyLinkedList<E> implements MyList<E> {
	/**
	* Method of adding elements to bidirectional linked list
	* @param element
	*/
	@Override
	public void add(E element) {
	}
	/**
	* Gets the element according to the specified location
	* @param index
	* @return
	*/
	@Override
	public E get(int index) {
		return null;
	}
	/**
	* Returns the number of elements
	* @return
	*/
	@Override
	public int size() {
		return 0;
	}
	/**
	* Deletes the element according to the specified location
	* @param index
	* @return
	*/
	@Override
	public E remove(int index) {
		return null;
	}
	public static void main(String[] args) {
	}
}

2.3.2.2 create node class

/**
* Defines the node object of the bidirectional linked list
*/
class Node<E>{
	E item;//Record element
	Node<E> prev;//Record previous node object
	Node<E> next;//Record the next node object
	Node(Node<E> prev,E item,Node<E> next){
		this.prev = prev;
		this.item = item;
		this.next = next;
	}
}

2.3.2.3 implement the method of adding elements

private Node head; //Record header node
private Node tail; //Record tail node
private int size; //Number of record elements
/**
* Method of adding elements to bidirectional linked list
* @param element
*/
@Override
public void add(E element) {
this.linkLast(element);
}
/**
* Add the node object to the tail of the bidirectional linked list
*/
private void linkLast(E element){
	//Get tail node
	Node t = this.tail;
	//Create node object
	Node<E> node = new Node<>(t,element,null);
	//Define the new node as the tail node
	this.tail = node;
	if(t == null){
		this.head = node;
	}else{
		t.next = node;
	}
		this.size++;
}

2.3.2.4 method of obtaining elements

/**
* Gets the element according to the specified location
* @param index
* @return
*/
@Override
public E get(int index) {
	//Check the validity of Index
	this.checkIndex(index);
	//Find node objects by location
	Node<E> node = this.getNode(index);
	return node.item;
}
/**
* Verify the validity of Index
*/
private void checkIndex(int index){
	if(!(index >= 0 && index < this.size)){
		throw new IndexOutOfBoundsException("Index: "+index+" Size:"+size);
		}
	}
	/**
	* Gets the specified node object according to the location
	*/
	private Node getNode(int index){
	//Judge which node the current position is closer to the head or tail
	if(index < (this.size >> 1)){
	Node node = this.head;
	for(int i=0;i<index;i++){
		node = node.next;
	}
		return node;
	}else{
		Node node = this.tail;
		for(int i=this.size-1;i>index;i--){
			node = node.prev;
	}
	return node;
	}
}

2.3.2.5 implement the method of deleting elements

/**
* Deletes the element according to the specified location
* @param index
* @return
*/
@Override
public E remove(int index) {
	//Verify the validity of the Index
	this.checkIndex(index);
	//Gets the node object according to the specified location
	Node<E> node = this.getNode(index);
	//Gets the element in the node object
	E item = node.item;
	//Judge whether the current node is a header node
	if(node.prev ==null){
	this.head = node.next;
	}else{
	//Complete the connection between the direct predecessor node of the current node and the direct successor node of the current node
	node.prev.next = node.next;
	}
	//Judge whether the current node is the tail node
	if(node.next == null){
		this.tail = node.prev;
	}else{
		//Complete the connection between the direct successor node of the current node and the direct predecessor node of the current node
		node.next.prev = node.prev;
	}
	//The current node disconnects from its direct predecessor node
	node.prev = null;
	//The current node disconnects from its immediate successor
	node.next = null;
	node.item = null;
	//Number of record elements
	this.size--;
	return item;
}

2.3.2.6 get the number of elements

/**
* Returns the number of elements
* @return
*/
@Override
public int size() {
	return this.size;
}

2.3.2.7 add elements to the header of the bidirectional linked list

/**
* Add an element to the head of a two-way linked list
*
*/
public void addFirst(E element){
this.linkFirst(element);
}
/**
* Add elements to the head of the linked list
*
*/
private void linkFirst(E element){
	//Get header node object
	Node head = this.head;
	Node node = new Node(null,element,head);
	//Define the new node as the head node
	this.head = node;
	//Judge whether there is a node in the current linked list. If not, the node is both the head node and the tail node
	if(head == null){
		this.tail = node;
	}else{
		head.prev = node;
	}
	//Number of record elements
	this.size++;
}

2.3.2.8 add elements to the tail of the bidirectional linked list

/**
* Add elements at the end of the linked list
* @param element
*/
public void addLast(E element){
	this.linkLast(element);
}

3, Tree structure

1 Introduction to tree structure

Tree structure is a nonlinear storage structure, which stores a set of data elements with "one to many" relationship.

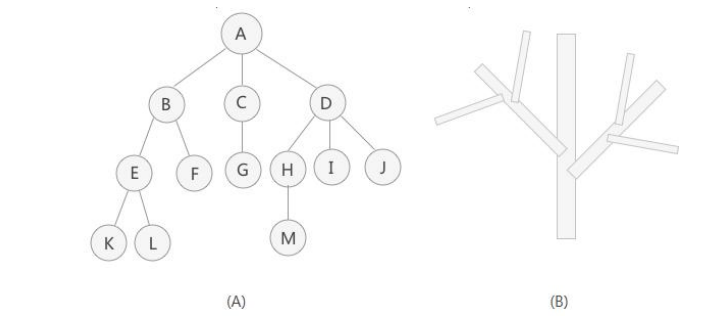
2 related terms of tree

2.1 node

Each data element stored in a tree structure is called a "node".

2.2 degree of node

The number of subtrees owned by a node.

2.3 degree of tree

The maximum number of layers of nodes in the tree.

2.4 leaf node

A node with a degree of 0 is also called a terminal node.

2.5 branch node

Nodes whose degree is not 0 are also called non terminal nodes or internal nodes.

2.6 children

It can also be called subtree or child node, which represents the direct node under the current node.

2.7 parents

It can also be called parent node, which represents the direct upper node of the current node.

2.8 root node

Nodes without parent nodes. There is only one root node in a tree structure.

2.9 ancestry

From all nodes above the current node.

2.10 descendants

All nodes under the current node.

2.11 brother

Children of the same parents.

3 Introduction to binary tree

Binary Tree is an important type of tree structure. The data structure abstracted from many practical problems is often in the form of Binary Tree. Even a general tree can be simply transformed into Binary Tree, and the storage structure and algorithm of Binary Tree are relatively simple, so Binary Tree is particularly important. The characteristic of Binary Tree is that each node can only have two subtrees at most, which can be divided into left and right.

3.1 binary tree classification

3.1.1 full binary tree

Full binary tree means that all nodes on each layer except the last layer have two child nodes.

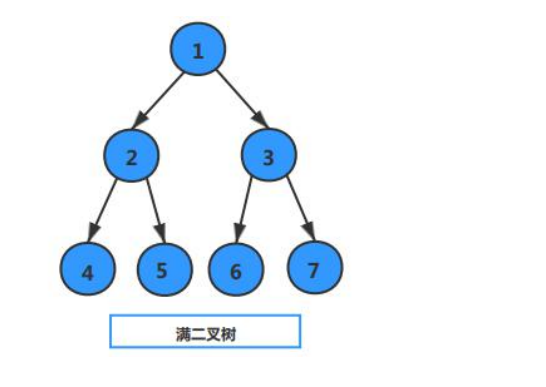
3.1.2 complete binary tree

For a complete binary tree, except that the last layer may be dissatisfied, all other layers reach the maximum number of nodes in this layer. If the last layer is dissatisfied, all nodes in this layer are in the left row.

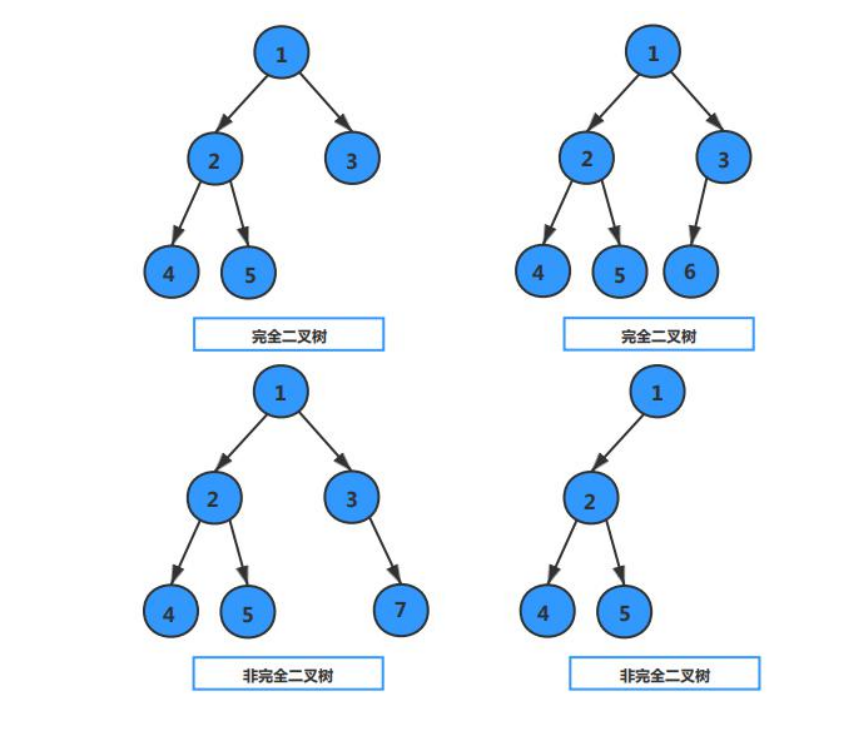
3.2 binary tree traversal

Traversal method of binary tree:

• Preorder traversal: root left right
• Middle order traversal: left root right
• Post order traversal: left right root
• Sequence traversal: traversal layer by layer from top to bottom

3.2.1 preorder traversal

Preorder traversal order: root left right

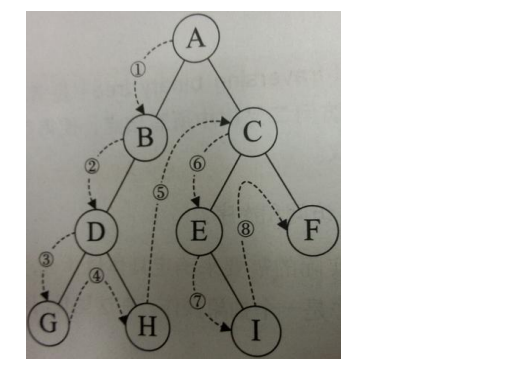
3.2.2 middle order traversal

Middle order traversal order: left root right

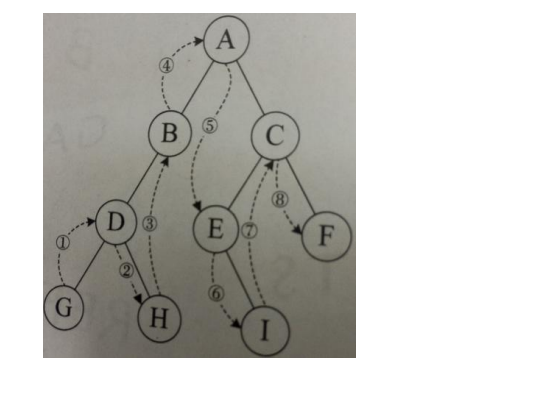
3.2.3 post order traversal

Post order traversal order: left right root

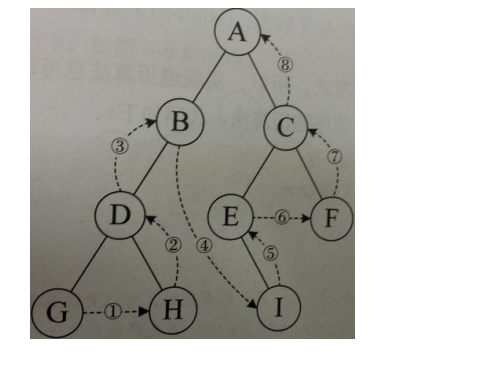
3.2.4 sequence traversal

Sequence traversal sequence:
Starting from the root node, access the left and right child nodes in turn, and then start from the left and right children to their child nodes in turn until the node is accessed.

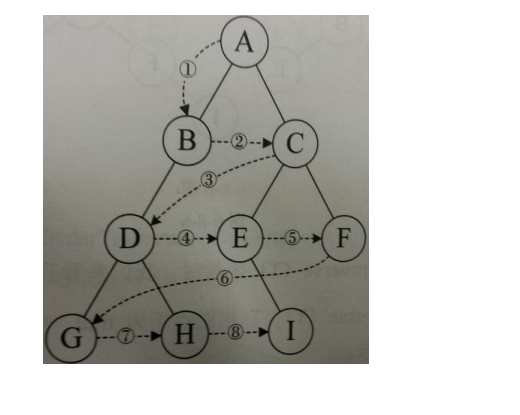
3.3 binary tree sorting

3.3.1 binary tree sorting analysis

Using the binary tree structure and traversal mode, the element sorting processing based on binary tree can be realized.

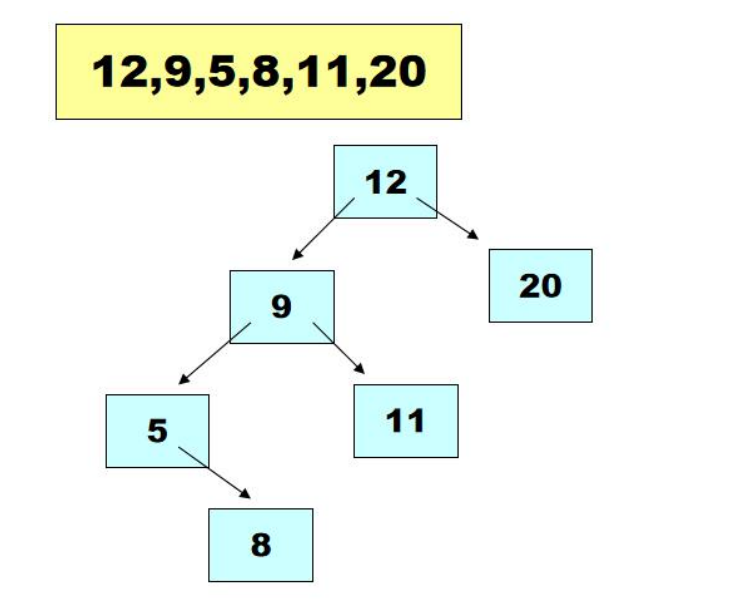
3.3.2 implementation of binary tree sorting

3.3.2.1 create a binary tree sorter class

/**
* A sorter for element sorting based on binary tree structure
*/
public class BinaryTreeSort<E extends Integer> {
	/**
	* Add element to sorter
	*/
	public void add(E element){
	}
	/**
	* Sort elements
	*/
	public void sort(){
	}
	public static void main(String[] args) {
	}
}

3.3.2.2 create node class

/**
* Define node class
*/
class Node<E extends Integer>{
	private E item;//Store elements
	private Node left;//Address of left subtree
	private Node right;//Address for storing right subtree
	Node(E item){
	this.item = item;
}
	/**
	* Add node
	*/
	public void addNode(Node node){
	//Complete the judgment between the elements in the new node and the elements in the current node
	//If the elements in the new node are smaller than those in the current node, the new node will be placed in the left subtree of the current node.
	if(node.item.intValue() < this.item.intValue()){
	if(this.left == null)
		this.left = node;
	else
		this.left.addNode(node);
	}else{
	//If the elements in the new node are larger than those in the current node, the new node will be placed in the current node
	In the right subtree of.
	if(this.right == null)
		this.right = node;
	else
		this.right.addNode(node);
	}
}
/**
* Traversing binary tree using middle order
*/
public void inorderTraversal(){
	//Find the node on the far left
		if(this.left != null)this.left.inorderTraversal();
		System.out.println(this.item);
		if(this.right != null)this.right.inorderTraversal();
	}
}

3.3.2.3 implement the method of adding elements to the sorter

/**
* Add element to sorter
*/
public void add(E element){
//Instantiate node object
Node<E> node = new Node<>(element);
//Judge whether there is a root node in the current binary tree. If there is no new node, then there is no root
if(this.root == null)
	this.root = node;
else
	this.root.addNode(node);
}

3.3.2.4 implement the sorting method in the sorter

/**
* Sort elements
*/
public void sort(){
	//Judge whether the root node is empty
	if(this.root == null)return ;
	this.root.inorderTraversal();
}

4 custom tree structure container

4.1 tree structure definition

The parent node of the current node can be found
The child nodes of the current node can be found
The sibling node of the current node can be found
The ancestor node of the current node can be found
Can find the descendants of the current node

4.2 user defined tree structure analysis

4.3 implement custom tree structure container

4.3.1 create a tree structure container class

/**
* Container for element storage based on tree structure
*/
public class MyTree<E> {
	/**
	* Add element to container
	*/
	public void add(E parent,E item){
	}
	/**
	* Gets the parent node of the current node
	*/
	public E getParent(E item){
		return null;
	}
	/**
	* Get the child nodes of the current node
	*/
	public List<E> getChild(E item){
		return null;
	}
	/**
	* Get the sibling node of the current node
	*/
	public List<E> getBrother(E item){
		return null;
	}
	/**
	* Get the ancestor node of the current node
	*/
	public List<E> getForefathers(E item){
		return null;
	}
	/**
	* Get the descendants of the current node
	*/
	public List<E> getGrandChildren(E item){
		return null;
	}
	public static void main(String[] args) {
	}
}

4.3.2 method of adding elements

private Map<E,E> map = new HashMap<>();//String--->String
private Map<E,List<E>> map2 = new HashMap<>();//String ---->List
	/**
	* Add element to container
	*/
	public void add(E parent,E item){
	//Complete the mapping between single nodes
	this.map.put(item,parent);
	//Complete the mapping between multiple nodes
	List<E> list = this.map2.get(parent);
	//Judge whether there are child nodes under the current node. If not, create a new List
	if(list == null){
		list = new ArrayList<>();
		this.map2.put(parent,list);
	}
	list.add(item);
}

4.3.3 get the parent and child nodes of the current node

4.3.3.1 get parent node

/**
* Gets the parent node of the current node
*/
public E getParent(E item){
	return this.map.get(item);
}

4.3.3.2 obtaining child nodes

/**
* Get the child nodes of the current node
*/
public List<E> getChild(E item){
	return this.map2.get(item);
}

4.3.4 get the sibling node of the current node

/**
* Get the sibling node of the current node
*/
public List<E> getBrother(E item){
	//Gets the parent node of the current node
	E parent = this.getParent(item);
	//Gets all the child nodes of the current parent node
	List<E> list = this.getChild(parent);
	List<E> brother = new ArrayList<>();
		if(list != null){
			brother.addAll(list);
			brother.remove(item);
		}
	return brother;
}

4.3.5 get the ancestor node of the current node

/**
* Get the ancestor node of the current node
*/
public List<E> getForefathers(E item){
	//Gets the parent node of the current node
	E parent = this.getParent(item);
	//End recursive boundary condition
	if(parent == null){
		return new ArrayList<>();
	}
	//Call recursively to get the parent node of the current node's parent node again
	List<E> list = this.getForefathers(parent);
	//Add all node elements recursively to the returned List
	list.add(parent);
	return list;
}

4.3.6 get the descendant nodes of the current node

/**
* Get the descendants of the current node
*/
public List<E> getGrandChildren(E item){
	//Store elements in all descendant nodes
	List<E> list = new ArrayList<>();
	//Get the child nodes of the current node
	List<E> child = this.getChild(item);
	//End recursive boundary condition
	if (child == null){
		return list;
	}
	//Traverse child nodes
	for(int i=0;i<child.size();i++){
		//Gets the element in the node
		E ele = child.get(i);
		List<E> temp = this.getGrandChildren(ele);
		list.add(ele);
		list.addAll(temp);
	}
	return list;
}

4.3.7 testing custom containers

public static void main(String[] args) {
	//Instantiate container
	MyTree<String> myTree = new MyTree<>();
	//Add element
	myTree.add("root","biology");
	myTree.add("biology","Botany");
	myTree.add("biology","animal");
	myTree.add("biology","Fungi");
	myTree.add("animal","vertebrate");
	myTree.add("animal","Chordate animal");
	myTree.add("animal","coelenterate");
	myTree.add("vertebrate","mammal");
	myTree.add("vertebrate","fish");
	myTree.add("mammal","cat");
	myTree.add("mammal","cattle");
	myTree.add("mammal","people");
	System.out.println("---------Get parent node---------");
	String parent = myTree.getParent("fish");
	System.out.println(parent);
	System.out.println("---------Get child nodes---------");
	
	List<String> child= myTree.getChild("animal");
	for(int i=0;i<child.size();i++){
		System.out.println(child.get(i));
	}
	System.out.println("---------Get sibling node---------");
	List<String> brother = myTree.getBrother("vertebrate");
	for(int i=0;i<brother.size();i++){
		System.out.println(brother.get(i));
	}
	System.out.println("---------Get ancestor node---------");
	List<String> foreFathers = myTree.getForefathers("people");
	for(int i=0;i<foreFathers.size();i++){
		System.out.println(foreFathers.get(i));
	}
	System.out.println("---------Get descendant node---------");
	List<String> grandChildren = myTree.getGrandChildren("root");
	for(int i =0;i<grandChildren.size();i++){
		System.out.println(grandChildren.get(i));
	}
}