Drawing out: we learned linear tables and trees earlier. The linear table is limited to the relationship between a direct precursor and a direct successor; The tree can only have one direct precursor, that is, the parent node. However, when we need to represent many to many relationships, we need to use the data structure of graph.
There are two representations of graphs: two-dimensional array representation (adjacency matrix); Linked list representation (adjacency list).
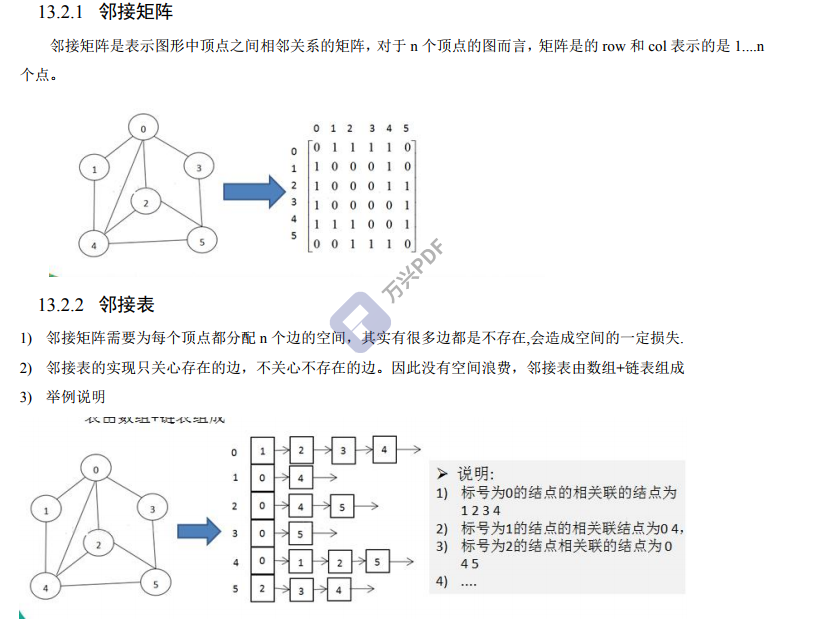
In the adjacency matrix, if two vertices are connected, it is 1; if they are not connected, it is zero.
Traversal of graph:
There are two strategies. 1. Depth First Search. 2. Breadth first search.
Depth first traversal idea: depth first traversal is a vertical cutting idea. The idea is to access the current vertex first, and then use this vertex as the initial vertex to access the first adjacent vertex of the vertex. It can be understood as follows: each time you access the current vertex, you first access the first adjacent vertex of the current vertex. Such an access strategy is to give priority to vertical mining, rather than horizontal access to all adjacent nodes of a node. It can be seen that depth first traversal needs to be realized through recursion.
Breadth first traversal idea: breadth first traversal is similar to a hierarchical search process. Breadth first traversal needs to use a queue to maintain the order of visited nodes, so as to access the adjacent nodes of these nodes in this order.
Next, let me give an example to illustrate the idea of depth first traversal

Next, let's talk about the breadth first traversal idea with the same example:

The difference between the two: depth first is to traverse to the end; Breadth first is like a net, step by step.
This is the main difference between the two
Steps of depth first traversal:
- Access the initial node v and mark node v as accessed.
- Find the first adjacent node w of node v.
- If w exists, continue with 4. If w does not exist, return to step 1 and continue from the next node of v.
- If W is not accessed, perform depth first traversal recursion on w (that is, treat w as another v, and then proceed to step 123)
- Find the next adjacent node of the w adjacent node of node v and go to step 3
Breadth first traversal steps:
- Access the initial node v and mark node v as accessed.
- Node v in queue
- When the queue is not empty, continue to execute, otherwise the algorithm ends.
- Out of the queue, get the queue header u.
- Find the first adjacent node w of node u.
- If the adjacent node w of node u does not exist, go to step 3; Otherwise, the loop performs the following three steps:
6.1 if node w has not been accessed, access node W and mark it as accessed.
6.2 node w entering the queue.
6.3 find the next adjacent node w of node u after the adjacent node W, and go to step 6.
The specific implementation code is attached. You can feel it carefully through the code.
package com.liu.chart;
import java.util.ArrayList;
import java.util.LinkedList;
/**
* @author liuweixin
* @create 2021-09-20 8:50
*/
//chart
public class VertexChart {
ArrayList<String> VertexList;
int[][] edges;//Used to store the relationship between vertices
int numOfEdges;//Indicates the number of edges
public static void main(String[] args) {
// String[] data = new String[]{"A", "B", "C", "D", "E"};
String[] data = new String[]{"1", "2", "3", "4", "5", "6", "7", "8"};
VertexChart vertexChart = new VertexChart(data.length);
for (String value : data) {
vertexChart.addVertex(value);
}
// vertexChart.addEdge(0,1,1);
// vertexChart.addEdge(0,2,1);
// vertexChart.addEdge(1,2,1);
// vertexChart.addEdge(1,3,1);
// vertexChart.addEdge(1,4,1);
vertexChart.addEdge(0, 1, 1);
vertexChart.addEdge(0, 2, 1);
vertexChart.addEdge(1, 3, 1);
vertexChart.addEdge(1, 4, 1);
vertexChart.addEdge(2, 5, 1);
vertexChart.addEdge(2, 6, 1);
vertexChart.addEdge(3, 7, 1);
vertexChart.addEdge(4, 7, 1);
vertexChart.addEdge(5, 6, 1);
vertexChart.show();
System.out.println();
vertexChart.dfs();//Depth first traversal: 1-2-4-8-5-3-6-7
System.out.println();
vertexChart.bfs();//Breadth first traversal: 1-2-3-4-5-6-7-8
}
public VertexChart(int VertexCount) {
edges = new int[VertexCount][VertexCount];
VertexList = new ArrayList<String>(VertexCount);
numOfEdges = 0;
}
/**
* Encapsulation of breadth first methods
*/
public void bfs(){
boolean[] isVisited = new boolean[VertexList.size()];
//The reason for adding this loop is that the data may be distributed on two or even more graphs, so we need to traverse all the data in breadth first
//If the data is distributed on a single graph, this cycle is not required
for (int i = 0; i < VertexList.size(); i++) {//Breadth first traversal of all data
if(!isVisited[i]){//Determine whether you have visited
bfs(isVisited,i);//Perform breadth first traversal
}
}
}
/**
*Breadth first
* @param isVisited Is it accessed
* @param i Initial Node
*/
public void bfs(boolean[] isVisited, int i){
int u;//Indicates the subscript corresponding to the head node of the queue
int w;//Adjacent node w
//Queue, which records the access order of nodes
LinkedList queue = new LinkedList();
//Access node and output node information
System.out.print(VertexList.get(i)+ " ");
//Mark as accessed
isVisited[i]=true;
//Add node to queue
queue.addLast(i);
while (!queue.isEmpty()){
//Fetch the subscript of the header node of the queue
u=(Integer)queue.removeFirst();
//Get the subscript w of the first adjacent node
w=getFirstNeighbor(u);
while (w!=-1){//find
//Have you visited
if(!isVisited[w]){
System.out.print(VertexList.get(w)+" ");
//Mark already accessed
isVisited[w]=true;
//Join the team
queue.addLast(w);
}
//Take u as the leading point and find the next adjacent contact after w
w=getNextNeighbor(u,w);//It shows breadth first
}
}
}
//Encapsulate the depth first traversal method
public void dfs() {
boolean[] isVisited = new boolean[VertexList.size()];
//The reason for adding this loop is that the data may be distributed on two or even more graphs, so we need to implement depth first traversal of all data
//If the data is distributed on a single graph, this cycle is not required
for (int i = 0; i < VertexList.size(); i++) {//Depth first traversal of all data
if(!isVisited[i]){//Determine whether you have visited
dfs(isVisited, 0);//Depth first
}
}
}
/**
* Depth first traversal
*
* @param isVisited Is it accessed
* @param i Initial Node
*/
public void dfs(boolean[] isVisited, int i) {
System.out.print(VertexList.get(i) + " ");
isVisited[i] = true;//Setting this point has been accessed
//Get the subscript of the first adjacent node of the node
int index = getFirstNeighbor(i);
while (index != -1) {//If the loop can come in, it indicates that there is a next adjacent node
if (!isVisited[index]) {//If the node has not been accessed
//Recursive traversal + backtracking
dfs(isVisited, index);
}
//If the node has been accessed
index = getNextNeighbor(i, index);
}
}
/**
* The next adjacent node is obtained according to the subscript of the adjacent node of the previous node
*
* @param v1
* @param v2
* @return
*/
public int getNextNeighbor(int v1, int v2) {
for (int i = v2 + 1; i < VertexList.size(); i++) {
if (edges[v1][i] > 0) {
return i;
}
}
return -1;
}
/**
* The first adjacent node of the subscript is obtained
*
* @param index
* @return If it is found, the subscript value is returned. If it is not found, it returns - 1
*/
public int getFirstNeighbor(int index) {
for (int i = 0; i < VertexList.size(); i++) {
if (edges[index][i] == 1) {
return i;
}
}
return -1;
}
/**
* Show adjacency matrix of graph
*/
public void show() {
for (int[] arr : edges) {
for (int data : arr) {
System.out.print(data + " ");
}
System.out.println();
}
}
/**
* Gets the number of vertices
*
* @return Returns the number of vertices
*/
public int getVexCount() {
return VertexList.size();
}
/**
* Get the number of edges
*
* @return Returns the number of edges
*/
public int getNumOfEdges() {
return numOfEdges;
}
/**
* Returns the relationship between the corresponding two vertices
*
* @param v1 Subscript of the first vertex
* @param v2 Subscript of the second vertex
* @return If 1 is returned, it indicates that it can be connected; If 0 is returned, it means it is not connected
*/
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
/**
* Gets the vertex value of the corresponding subscript
*
* @param index Corresponding subscript
* @return Returns the vertex value
*/
public String getVertex(int index) {
return VertexList.get(index);
}
/**
* Store the vertex data in the List
*
* @param data
*/
public void addVertex(String data) {
VertexList.add(data);
}
/**
* Represents the relationship between vertices
*
* @param v1 Indicates the subscript of the point, that is, the number of vertices
* @param v2 The lower edge corresponding to the second vertex
* @param weight The relationship between the two. If it is 1, it means that the two are connected; If it is 0, it means that the two are not connected.
*/
public void addEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
}