preface
Hello, I'm bigsai. I haven't seen you for a long time. I miss you very much!
Recently, a little friend complained to me that he didn't meet LRU. He said that he knew that he had been asked about LRU a long time ago, but he thought he wouldn't meet it, so he didn't prepare for it for the time being.
Unfortunately, I really got it! His mood at the moment can be proved by a picture:

He said that he finally stumbled to write an inefficient LRU, and the interviewer didn't look very satisfied... Then he really GG.
To prevent this pit from being encountered again in the future, I stepped on it with you today. At the beginning, I also used a more common method for this problem, but although a good method is not very difficult, it took me a long time to think of it. Although it took too much time and was not worth it, I finally figured it out and shared this process with you (only from the perspective of algorithm, not from the perspective of operating system).

Understand LRU
To design an LRU, do you need to know what an LRU is?
LRU, the full English name is Least Recently Used, which translates into the longest unused algorithm. It is a commonly used page replacement algorithm.
When it comes to page replacement algorithm, it has a great relationship with OS. We all know that the speed of memory is relatively fast, but the capacity of memory is very limited. It is impossible to load all pages into memory, so we need a strategy to pre put commonly used pages into memory.
However, no one knows which memory the process will access next time, and can't effectively know (we don't have the function to predict the future at present), so some page replacement algorithms are only idealized but can't be realized (yes, it's the optimal replacement algorithm). Then the common algorithms that must be returned are FIFO (first in, first out) and LRU (not used for the longest time recently).
LRU is not difficult to understand. It is to maintain a container with a fixed size. The core is get() and put().

Let's take a look at the two operations of LRU:
Initialization: LRUCache(int capacity) initializes LRU cache with positive integer as capacity.
Query: get(int key). Find out whether there is a value corresponding to the current key from your designed data structure. If so, return the corresponding value, and update the key record as the most recently used. If not, return - 1.
Insert / update: put(int key,int value) may insert a key value or update a key value. If the key value is already stored in the container, only the corresponding value value needs to be updated and marked as the latest. If the container does not have this value, consider whether the container is full. If it is full, delete the pair of key values that have not been used for the longest time.
The process here can give you an example, for example
Capacity size is 2: [ "put", "put", "get", "put","get", "put","get","get","get"] [ [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
The process is as follows:
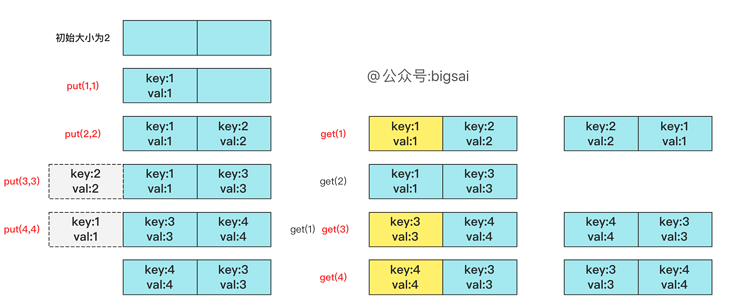
Details that are easy to ignore include:
- put() has an updated operation. For example, put(3,3),put(3,4) will update the operation with key 3.
- get() may not be able to query, but it will also update the longest unused order.
- If the container is not full, put may update but will not delete it; if the container is full and put is inserted, consider deleting the longest unused key value.
What should we do with the above rule?
If you only use a List similar to a List, you can store key value pairs in sequence. We think it is relatively long in front of the List (0 subscript is the front), and it is relatively new after the List. We may design the following operations:
If you want to get:
Traverse the List one by one to check whether there is a key value pair of the key. If there is, directly return the value of the corresponding key. If not, return - 1
If you want to put:
Traverse the List. If there is a key value pair for the key, delete the key value decisively, and finally insert the key value pair uniformly at the end.
If there is no corresponding key and the List container has reached the full, delete the key value in the first position decisively.
Using a List may require two (one key and one value) or a List of Node nodes (key and value are attributes). Consider this time complexity:
put operation: O(n) and get operation: O(n) both operations need the linear complexity of the enumeration list. The efficiency is true. It's a little hip pulling. It certainly can't. I won't write such code.

Hash initial optimization
From the above analysis, we can confidently write the LRU, but now we need to consider an optimization.
If we introduce the hash table into the program, there must be some optimization. If we store the key value in the hash table, the operation of querying whether it exists can be optimized to O(1), but the complexity of deleting, inserting or updating the location may still be O(n). Let's analyze it together:
The longest unused sequence must be an ordered sequence to store, either a sequential list (array) or a linked list. If the ArrayList implemented by an array stores the longest unused sequence.
If the ArrayList deletes the longest unused (first) key value, the new key is hit and becomes the latest used (delete first and then insert the end) operation is O(n).
Similarly, most of the operations of LinkedList are also O(n), such as deleting the first element because of the data structure O(1).
You find that your optimization space is actually very, very small, but there is still progress. You are just stuck. You don't know how to optimize the Double O(1) operation. I'll release the code of this version for your reference (if you ask in the interview, you can't write it like this)
class LRUCache {
Map<Integer,Integer>map=new HashMap<>();
List<Integer>list=new ArrayList<>();
int maxSize;
public LRUCache(int capacity) {
maxSize=capacity;
}
public int get(int key) {
if(!map.containsKey(key))//Does not exist return - 1
return -1;
int val=map.get(key);
put(key,val);//It's important to update the location to the latest!
return val;
}
public void put(int key, int value) {
//If the key exists, you can update it directly
if (map.containsKey(key)) {
list.remove((Integer) key);
list.add(key);
} else {//If it does not exist, insert it to the last, but if the capacity is full, delete the first (longest)
if (!map.containsKey(key)) {
if (list.size() == maxSize) {
map.remove(list.get(0));
list.remove(0);
}
list.add(key);
}
}
map.put(key, value);
}
}Hash + double linked list
As we know above, we can directly find this element with hash, but it is difficult to delete! It is very laborious to use List.
In more detail, due to the deletion of List, the deletion and insertion of Map is still very efficient.
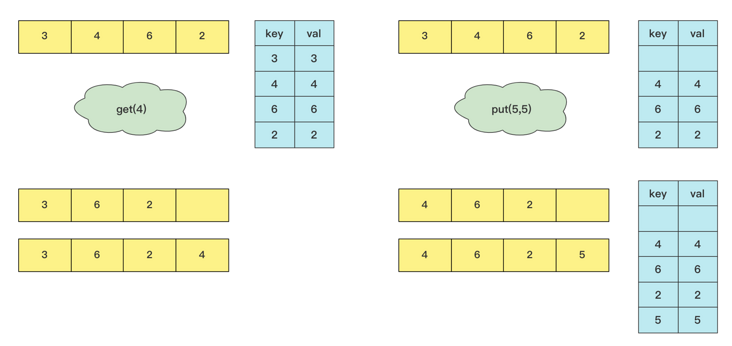
In the above case, we hope to quickly delete any element in the List with high efficiency. What should we do if we can only locate it at most with the help of hash, but can't delete it?
Hash + double linked list!
We save the key Val data into a Node class, and then each Node knows the left and right nodes and directly stores it in the Map when inserting the linked list, so that the Map can directly return the Node when querying. The double linked list knows the left and right nodes and can directly delete the Node in the double linked list.
Of course, for efficiency, the double linked list implemented here has the leading node (the head pointer points to an empty node to prevent exceptions such as deletion) and the tail pointer.
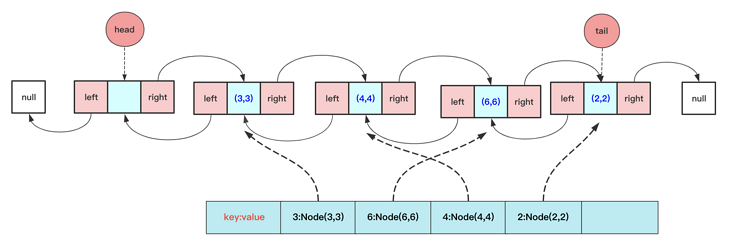
In this case, you need to be able to write a linked list and a double linked list. The addition, deletion and modification of the double linked list have been clearly written. Don't worry, guys. I've sorted it out here:
Single linked list: https://mp.weixin.qq.com/s/Cq98GmXt61-2wFj4WWezSg
Double linked list: https://mp.weixin.qq.com/s/h6s7lXt5G3JdkBZTi01G3A
That is, you can directly get the corresponding Node in the double linked list through HashMap, and then delete it according to the relationship between the front and back nodes. During this period, you can consider some special cases such as null, tail pointer deletion and so on.
The specific implementation code is:
class LRUCache {
class Node {
int key;
int value;
Node pre;
Node next;
public Node() {
}
public Node( int key,int value) {
this.key = key;
this.value=value;
}
}
class DoubleList{
private Node head;// Head node
private Node tail;// Tail node
private int length;
public DoubleList() {
head = new Node(-1,-1);
tail = head;
length = 0;
}
void add(Node teamNode)// Default tail node insertion
{
tail.next = teamNode;
teamNode.pre=tail;
tail = teamNode;
length++;
}
void deleteFirst(){
if(head.next==null)
return;
if(head.next==tail)//If the deleted one happens to be tail, notice that the tail pointer moves in front
tail=head;
head.next=head.next.next;
if(head.next!=null)
head.next.pre=head;
length--;
}
void deleteNode(Node team){
team.pre.next=team.next;
if(team.next!=null)
team.next.pre=team.pre;
if(team==tail)
tail=tail.pre;
team.pre=null;
team.next=null;
length--;
}
public String toString() {
Node team = head.next;
String vaString = "len:"+length+" ";
while (team != null) {
vaString +="key:"+team.key+" val:"+ team.value + " ";
team = team.next;
}
return vaString;
}
}
Map<Integer,Node> map=new HashMap<>();
DoubleList doubleList;//Storage order
int maxSize;
LinkedList<Integer>list2=new LinkedList<>();
public LRUCache(int capacity) {
doubleList=new DoubleList();
maxSize=capacity;
}
public void print(){
System.out.print("maplen:"+map.keySet().size()+" ");
for(Integer in:map.keySet()){
System.out.print("key:"+in+" val:"+map.get(in).value+" ");
}
System.out.print(" ");
System.out.println("listLen:"+doubleList.length+" "+doubleList.toString()+" maxSize:"+maxSize);
}
public int get(int key) {
int val;
if(!map.containsKey(key))
return -1;
val=map.get(key).value;
Node team=map.get(key);
doubleList.deleteNode(team);
doubleList.add(team);
return val;
}
public void put(int key, int value) {
if(map.containsKey(key)){// This key already exists. Delete it and update it regardless of its length
Node deleteNode=map.get(key);
doubleList.deleteNode(deleteNode);
}
else if(doubleList.length==maxSize){//Does not contain and is less than
Node first=doubleList.head.next;
map.remove(first.key);
doubleList.deleteFirst();
}
Node node=new Node(key,value);
doubleList.add(node);
map.put(key,node);
}
}
In this way, a get and put LRU with O(1) complexity is written!
Epilogue
After reading the problem solution, I found that LinkedHashMap in Java is almost this data structure! A few lines to solve, but the general interviewer may not agree. He still hopes that everyone can write a double linked list by hand.
class LRUCache extends LinkedHashMap<Integer, Integer>{
private int capacity;
public LRUCache(int capacity) {
super(capacity, 0.75F, true);
this.capacity = capacity;
}
public int get(int key) {
return super.getOrDefault(key, -1);
}
public void put(int key, int value) {
super.put(key, value);
}
@Override
protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
return size() > capacity;
}
}Although hash + double linked list came up with it without looking at the problem solution, it really took a long time to think of this point. It was really rare in the past. Efficient handwritten LRU is really and completely mastered today!
However, in addition to LRU, other page replacement algorithms, whether written or interview, are also very high-frequency. Please comb them yourself when you have time.
First official account: bigsai reprint, please place the author and the original (this) link, daily attendance, welcome to play card together, learning and communication!