Binary tree is a common data structure in our daily learning. During the interview and study, we will inevitably encounter some algorithm problems related to binary tree. Today, I brought you some classic binary tree basic algorithm problems. Let's have a look!
catalogue
1. Check whether the two trees are the same
3. Maximum depth of binary tree
7. Construct a binary tree according to the pre order and middle order
1. Check whether the two trees are the same
① Title Description
Give you the root nodes p # and q of two binary trees, and write a function to check whether the two trees are the same. If two trees are structurally identical and the nodes have the same value, they are considered to be the same. (source: LeetCode)
Example: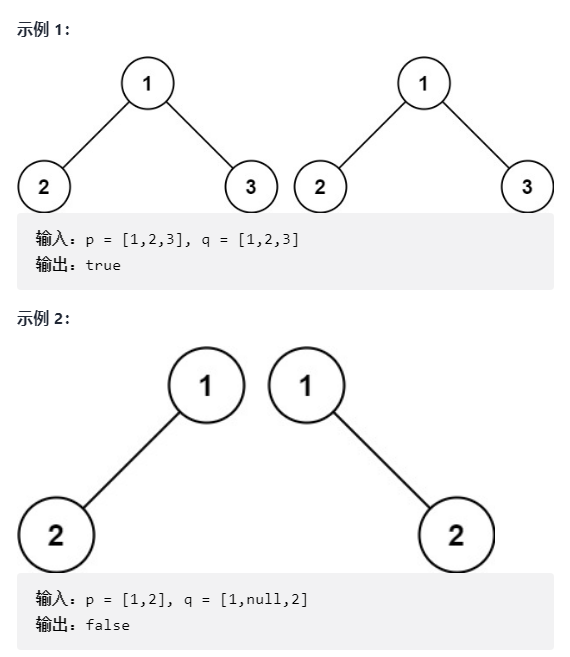
② train of thought analysis
According to the description of the topic, when we check whether the two binary trees are the same, we can first check whether the structure is the same. Then it can be basically divided into the following situations:
I One of the root nodes of the two trees is empty and the other is not: false
II Both trees are empty: true
III Neither tree is empty:
1. Same value: check subtree
2. Different values: false
③ Problem solving code
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p != null && q == null) {
return false;
} else if(p == null && q != null) {
return false;
}else if(p == null && q == null) {
return true;
}
if(p.val != q.val) {
return false;
}
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}2. A subtree of another tree
① Title Description
Here are two binary trees, root and subRoot. Check whether the root contains subtrees with the same structure and node values as the subRoot. If it exists, return true; Otherwise, false is returned. A subtree of a binary tree tree includes a node of the tree and all descendants of this node. A tree can be regarded as its own. (source: LeetCode)
Example:
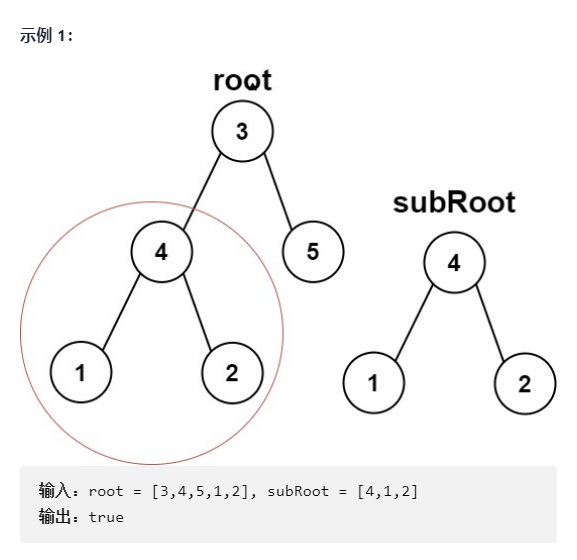
② train of thought analysis
According to the title description, we can divide the following steps when checking whether the subRoot is a root subtree:
I Check whether the two trees are the same (the code is the first question)
1. Same: true
2. Differences:
① Judge whether the root is null (if not, the null pointer may be abnormal if the left and right subtrees are referenced below)
② Recursive self left subtree and right subtree
③ Problem solving code
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(isSametree(root, subRoot)) {
return true;
} else if(root == null) {
return false;
}
return isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
}
public static boolean isSametree(TreeNode p, TreeNode q) {
if(p == null && q != null || p != null && q == null) {
return false;
} else if(p == null && q == null) {
return true;
}
if(p.val != q.val) {
return false;
}
return isSametree(p.left, q.left) && isSametree(p.right, q.right);
}3. Maximum depth of binary tree
① Title Description
Given a binary tree, find its maximum depth. The depth of the binary tree is the number of nodes on the longest path from the root node to the farthest leaf node. Note: leaf nodes refer to nodes without child nodes. (source: LeetCode)
Example:

② train of thought analysis
According to the description of the topic, the first thing we think of should be sequence traversal, and the number of layers can be counted, but the sequence seems to be a little useful here. We can think like this: if a tree traverses to the left, it will return 0 if it traverses to an empty node. At the same time, if it traverses to the right, it will also return 0 if it encounters an empty node; Then, when the leaf node traverses down, the left and right are empty, so the depth of the subtree should be only the leaf node itself. Another case: if one of the left and right is not 0 or neither is 0, then we should take its maximum value. Let's sort out our ideas:
I Verify that root is empty
1. Null: returns 0
2. Not empty: recursively calculate the depth of the left and right subtrees
① Returns the maximum depth of the left and right subtrees plus the current root node itself
③ Problem solving code
public int maxDepth(TreeNode root) {
if(root == null) {
return 0;
}
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return Math.max(left, right) + 1;
}4. Balanced binary tree
① Title Description
Given a binary tree, judge whether it is a highly balanced binary tree. In this question, a height balanced binary tree is defined as: the absolute value of the height difference between the left and right subtrees of each node of a binary tree does not exceed 1. (source: LeetCode)
Example:
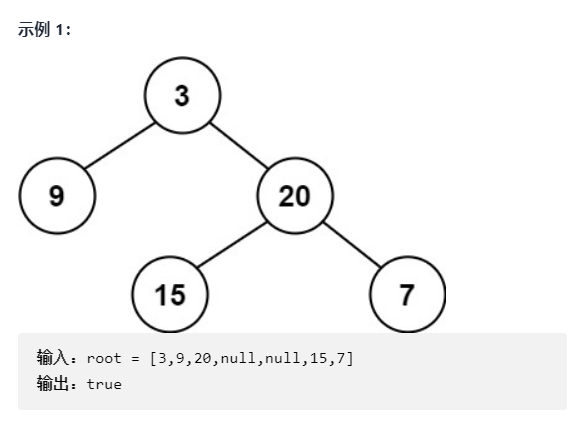
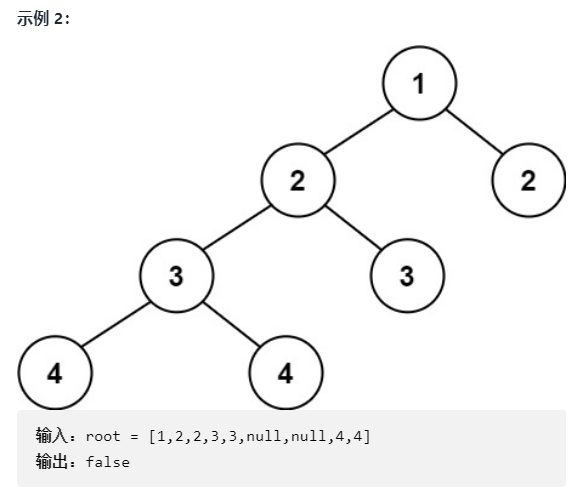
② train of thought analysis
We first check whether the root node is empty. If the root node is not empty, we ask whether the left and right subtrees meet the definition of balanced binary tree. Note: if a tree is a balanced binary tree, its subtree must be a balanced binary tree. After knowing this truth, we can recursively check the subtree. If it is not satisfied, it means that the whole tree is not a balanced binary tree.
I Check whether the root is empty
Null: returns true;
Not empty:
1. Recursively calculate the depth of left and right subtrees
2. Judge whether the left and right subtrees are greater than 0 and whether the depth difference between the left and right subtrees is less than 2
Less than 2:
①. Returns the current subtree depth
Greater than or equal to 2:
① Return - 1
If the final return value is a positive number, it represents a balanced binary tree
③ Problem solving code
public boolean isBalanced(TreeNode root) {
if(root == null) {
return true;
}
return high(root) >= 0;
}
public int high(TreeNode root) {
if(root == null) {
return 0;
}
int left = high(root.left);
int right = high(root.right);
if(left >= 0 && right >= 0 && Math.abs(left - right) < 2) {
return Math.max(left, right) + 1;
} else {
return -1;
}
}5. Symmetric binary tree
① Title Description
Give you the root node of a binary tree # root and check whether it is axisymmetric. (source: LeetCode)
Example:
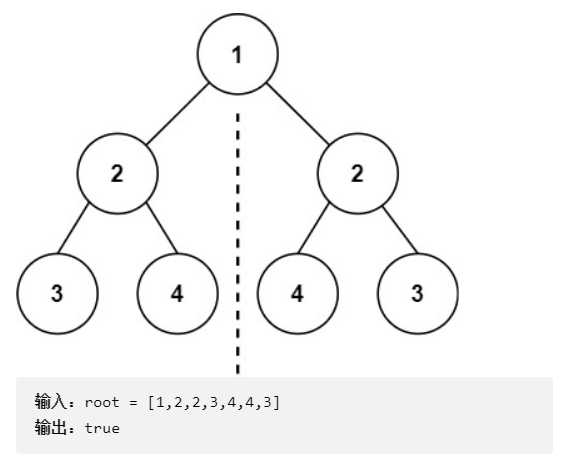
② thinking analysis
This problem is relatively simple. You only need to recurse the left and right subtrees, first judge the empty situation, and then judge whether the values are the same. If you find that it is not satisfied, you can directly return false.
③ Problem solving code
public boolean isSymmetric(TreeNode root) {
if(root == null) {
return true;
}
return isS(root.left, root.right);
}
public static boolean isS(TreeNode r1, TreeNode r2) {
if(r1 == null && r2 != null || r1 != null && r2 == null) {
return false;
}
if(r1 == null && r2 == null) {
return true;
}
if(r1.val != r2.val) {
return false;
}
return isS(r1.left, r2.right) && isS(r1.right, r2.left);
}6. Recent public ancestors
① Title Description
Given a binary tree, find the nearest common ancestor of two specified nodes in the tree. The definition of nearest common ancestor is: "for two nodes p and q with root tree T, the nearest common ancestor is expressed as a node X. if x is the ancestor of p and q and the depth of X is as large as possible, a node can also be its own ancestor. (source: LeetCode))
Example:
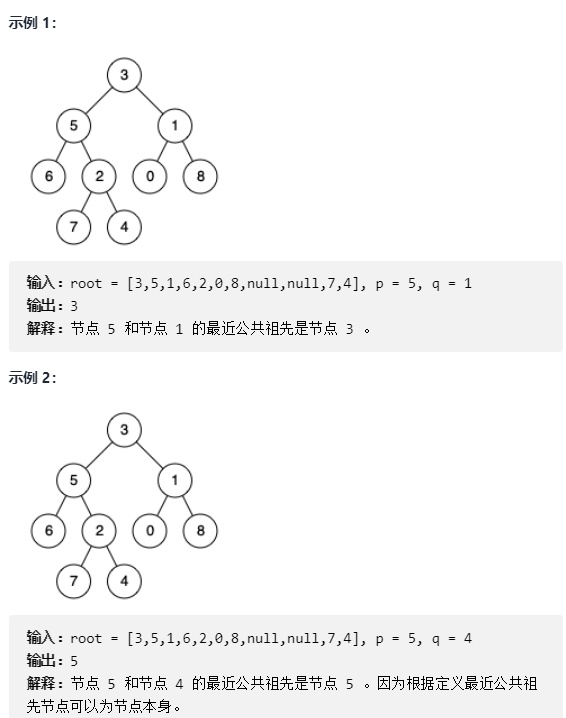
② Train of thought analysis
We first judge whether the current root node is empty. If the root node is empty, we directly return the empty node, indicating that the ancestor node cannot be found. If the current root node is not empty, we judge whether the root node is the same as a node we are looking for. We can divide the root node into three categories: 1 p. q two nodes are distributed in the left and right subtrees of a node, then the node is their nearest common ancestor. 2.p is the common ancestor of q. 3.q is the common ancestor of P.
I Determine whether root is empty:
1. Null: returns null
2. Not empty:
① Judge whether it is equal to one of p or q. if it is equal, it will directly return to the current node
② Unequal, start traversing the subtree left and right to judge which side p and q are on;
③ According to the return value, if both the left and right returns are empty, it means that it is not in the tree, and we also return empty. There is a non empty value on the left and right. Return a non empty value. If the left and right are not empty, it means that the current node is the ancestor node and returns directly.
③ Problem solving code
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) {
return null;
}
if(root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null && right != null) {
return right;
} else if(left != null && right == null) {
return left;
} else if(left == null && right == null) {
return null;
}
return root;
}In addition, there is another way to solve the problem: find out the path of the tree to p and q, and then convert it into a linked list to find the common intersection;
code:
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) {
return root;
}
Stack<TreeNode> sta1 = new Stack<>();
Stack<TreeNode> sta2 = new Stack<>();
findPath(root, p, sta1);
findPath(root, q, sta2);
int size = Math.abs(sta1.size() - sta2.size());
if(sta1.size() > sta2.size()) {
for(int i = 0; i < size; i++) {
sta1.pop();
}
} else {
for(int i = 0; i < size; i++) {
sta2.pop();
}
}
TreeNode ance = null;
while(sta1.size() != 0) {
TreeNode t1 = sta1.pop();
TreeNode t2 = sta2.pop();
if(t1 == t2) {
ance = t1;
break;
}
}
return ance;
}
public static boolean findPath(TreeNode root, TreeNode tar, Stack<TreeNode> sta) {
if(root == null) {
return false;
}
if(root == tar) {
sta.push(root);
return true;
}
sta.push(root);
boolean bool = findPath(root.left, tar, sta);
if(bool) {
return true;
} else {
bool = findPath(root.right, tar, sta);
}
if(bool) {
return true;
}
sta.pop();
return false;
}7. Construct a binary tree according to the pre order and middle order
① Title Description
Given two integer arrays pre and in, where pre is the preorder traversal of the binary tree and in is the inorder traversal of the same tree, please construct the binary tree and return its root node. (source: LeetCode)
Example:
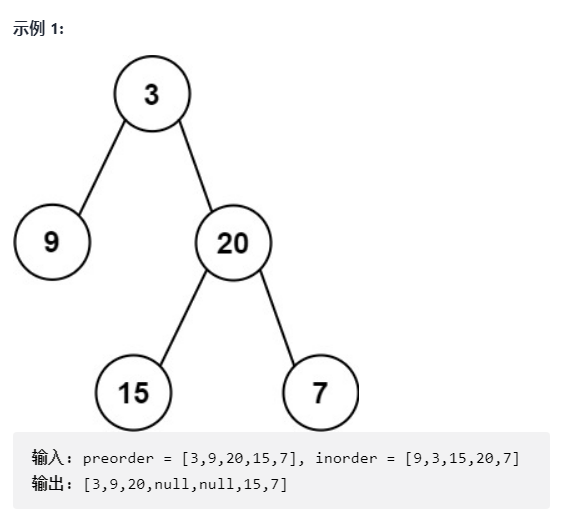
② train of thought analysis
We should first understand two things: 1 Preorder traversal is a collection of all roots 2 If a specified root is found in the middle order traversal, the middle order traversal of its left subtree is on the left and the middle order traversal of the right tree is on the right. According to the above conclusion: we can define two references. The first one starts from the subscript 0 of the former ordinal number group, and the second one finds the value of the first reference in the middle order sequence, that is, the value of the root. Then the middle order sequence is divided into left and right parts, which are matched with the left and right subtrees with just roots. And so on.
③ Problem solving code
int x = 0;
public TreeNode buildTree(int[] pre, int[] in) {
int left = 0;
int right = in.length - 1;
int val = pre[x];
x++;
int pivot = find(in, val, left, right);
if(pivot == -1) {
return null;
}
TreeNode cur = new TreeNode(val);
cur.left = build(pre, in, left, pivot - 1);
cur.right = build(pre, in, pivot + 1, right);
return cur;
}
public TreeNode build(int[] pre, int[] in, int left, int right) {
if(left > right) {
return null;
}
int val = pre[x];
x++;
int pivot = find(in, val, left, right);
if(pivot == -1) {
return null;
}
TreeNode cur = new TreeNode(val);
cur.left = build(pre, in, left, pivot - 1);
cur.right = build(pre, in, pivot + 1, right);
return cur;
}
public int find(int[] in, int val, int left, int right) {
for(int i = left; i <= right; i++) {
if(in[i] == val) {
return i;
}
}
return -1;
}The above is all the content of today. It's not easy to create. If you like it, please praise it!