1, Types of binary trees

1. Full binary tree

Except that the last layer has no child nodes, all nodes on each layer have two child node binary trees (if the depth is k, there are 2^k-1 nodes).

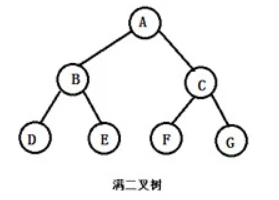
2. Complete binary tree

Let the depth of a binary tree be H. Except for layer h, the number of nodes in other layers reaches the maximum, and all nodes in layer H (the lowest layer) are continuously concentrated on the far left. This layer contains 1~ 2^h -1 nodes..

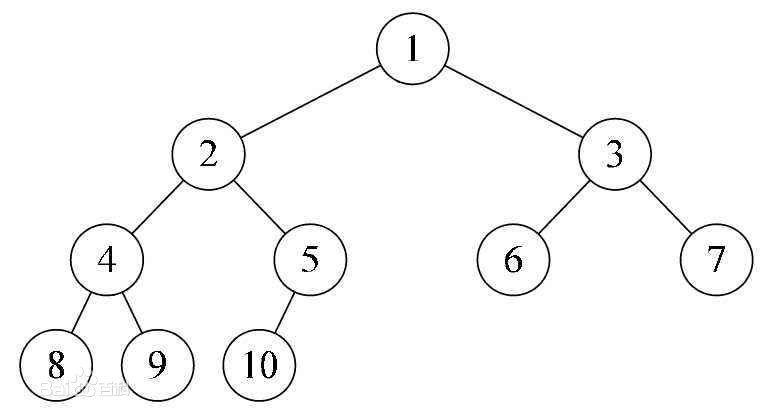
3. Binary search tree (binary search tree, binary sort tree)

Binary search tree is a numerical and ordered tree. If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node; If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of its root node; Its left and right subtrees are also binary sort trees.

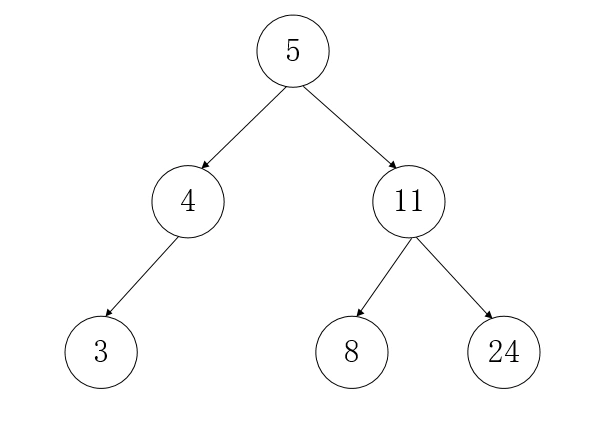
The binary search tree will have balance problems:

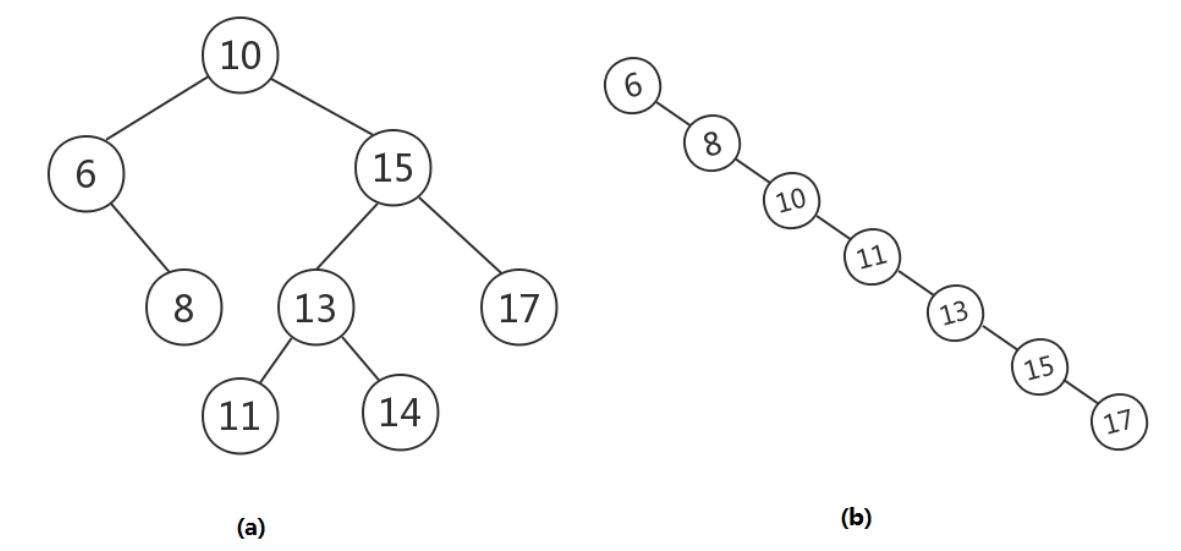
After multiple insertions and deletions, the binary search tree may lead to the structure of the above right figure: the search performance is already linear. Therefore, when using the binary search tree, we should also consider maintaining the structure of the above left figure as much as possible and avoiding the structure of the above right figure, that is, the so-called "balance" problem.

In order to solve this situation, the balanced binary search tree that I will talk about below appears.  

4. Balanced binary search tree (AVL tree)

AVL tree also stipulates that the left node is smaller than the root node and the right node is larger than the root node. It also stipulates that the height difference between the left subtree and the right subtree shall not exceed 1, which ensures that it will not become a linear linked list. AVL tree mainly solves the balance problem through left rotation and right rotation.

2, Creation of binary tree

//Initialization list form, initialization node
struct TreeNode{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode():val(0),left(nullptr),right(nullptr){}
    TreeNode(int x):val(x),left(nullptr),right(nullptr){}
    TreeNode(int x,TreeNode* left,TreeNode* right):val(x),left(left),right(right){}
};

//Construction of complete binary tree based on array
TreeNode *creatMytree(vector<int>& Mytree,int index,int len){
    if(index>=len)  return nullptr;
    TreeNode *t=new TreeNode(Mytree[index]);
    t->left=creatMytree(Mytree,index*2+1,len);
    t->right=creatMytree(Mytree,index*2+2,len);
    return t;
}

//Create any binary tree according to the previous traversal
TreeNode* deserialize_dfs(list<string>& dataArray){
    if(!dataArray.size() ) return nullptr;
    if(dataArray.front()=="None"){
        dataArray.erase(dataArray.begin());
        return nullptr;
    }
    TreeNode* node=new TreeNode(stoi(dataArray.front()));
    dataArray.erase(dataArray.begin());
    node->left=deserialize_dfs(dataArray);
    node->right=deserialize_dfs(dataArray);
    return node;
}

int main()
{
    //Create a complete binary tree from an array
    vector<int> Mytree={5,4,6,1,2,7,8};
    int len=Mytree.size();
    TreeNode *root=creatMytree(Mytree,0,len);

    //Create any binary tree according to the previous traversal
    list<string> dataArray={"1","2","4","None","None","None","3","None","None"};
    TreeNode *root1=deserialize_dfs(dataArray);

    getchar();
    return 0;
}

3, Traversal of binary tree

There are several ways to traverse a binary tree:

1. Depth first traversal

Preorder traversal (recursive method, iterative method): 5 4 1 2 6 7 8

Middle order traversal (recursive method, iterative method): left, middle and right # 1 4 2 5 7 6 8

Post order traversal (recursive method, iterative method): left and right middle 1 2 4 7 8 6 5

2. Breadth first traversal

Hierarchical traversal (iterative method): 5 4 6 1 2 7 8

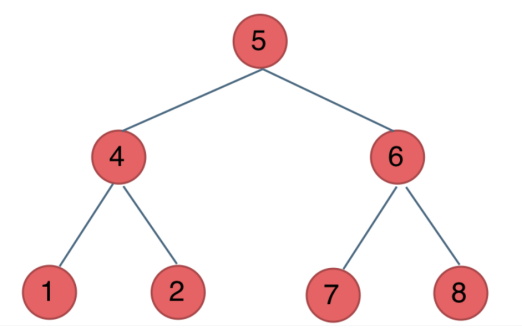
The code is as follows:

//Preorder traversal: left and right
//1. Recursive method
void preorderTraversal(TreeNode *cur,vector<int>& res){
    if(!cur) return;
    res.push_back(cur->val);
    preorderTraversal(cur->left,res);
    preorderTraversal(cur->right,res);
}
//2. Iterative method
void preorderStk(TreeNode *cur,vector<int>& res){
    stack<TreeNode*> stk;
    while(cur || !stk.empty()){
        while(cur){
            res.push_back(cur->val);    //in
            stk.push(cur);
            cur=cur->left;  //Left
        }
        cur=stk.top();
        stk.pop();
        cur=cur->right; //right
    }
    
}

//Middle order traversal: left, middle and right
//1. Recursive method
void inorderTraversal(TreeNode *cur,vector<int>& res){
    if(!cur) return;
    inorderTraversal(cur->left,res);
    res.push_back(cur->val);
    inorderTraversal(cur->right,res);
}
//2. Iterative method
void inorderStk(TreeNode *cur,vector<int>& res){
    stack<TreeNode*> stk;
    while(cur || !stk.empty()){
        while(cur){
            stk.push(cur);
            cur=cur->left;  //Left
        }
        cur=stk.top();
        stk.pop();
        res.push_back(cur->val);    //in
        cur=cur->right; //right
    }
    
}

//Post order traversal: left and right middle
//1. Recursive method
void postorderTraversal(TreeNode *cur,vector<int>& res){
    if(!cur) return;
    postorderTraversal(cur->left,res);
    postorderTraversal(cur->right,res);
    res.push_back(cur->val);
}
//2. Iterative method
void postorderStk(TreeNode *cur,vector<int>& res){
    stack<TreeNode*> stk;
    TreeNode* pre;
    while(cur || !stk.empty()){
        while(cur){
            stk.push(cur);
            cur=cur->left;  //Left
        }
        cur=stk.top();
        stk.pop();
        if(cur->right==nullptr || cur->right==pre){//cur can be put into res only when the right node is empty or res has been put into the right node before
            res.push_back(cur->val);    //in
            pre=cur;
            cur=nullptr; //Avoid repeated placement of cur
        }
        else{
            stk.push(cur);//If there are still nodes in the right subtree that have not been traversed, cur will be put on the stack again
            cur=cur->right; //right
        }
    }
    
}

//level traversal 
vector<vector<int>> levelOrder(TreeNode *root){
    vector<vector<int>> res;
    vector<int> temp;
    queue<TreeNode*> q;
    q.push(root);
    while(!q.empty()){
        int size=q.size();
        for(int i=0;i<size;i++){
            TreeNode *node=q.front();
            q.pop();
            if(node->left){
                q.push(node->left);
            }
            if(node->right){
                q.push(node->right);
            }
            temp.push_back(node->val);
        }
        res.push_back(temp);
        temp.clear();
    }
    return res;
} 

4, Common binary tree related questions

101. Symmetric binary tree

//Judge whether it is a symmetric binary tree
class Solution {
public:
    bool compare(TreeNode* l,TreeNode* r){
        if(!l&&!r) return true;
        else if(!l||!r) return false;
        return (l->val==r->val) && compare(l->left,r->right) && compare(l->right,r->left);
    }
    bool isSymmetric(TreeNode* root) {
        return compare(root,root);
    }
};

104. Maximum depth of binary tree 

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root) return 0;
        return max(maxDepth(root->left),maxDepth(root->right))+1;
    }
};

226. Flip binary tree

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root) return nullptr;
        swap(root->left,root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }
};

110. Balanced binary tree 

//Judge whether it is a balanced binary tree
class Solution {
public:
    int depth(TreeNode* root){
        if(!root) return 0;
        return max(depth(root->left),depth(root->right))+1;
    }
    bool isBalanced(TreeNode* root) {
        if(!root) return true;
        return (abs(depth(root->left)-depth(root->right))<=1) && isBalanced(root->left) && isBalanced(root->right);
    }
};

98. Verify binary search tree

class Solution {
public:
    bool search(TreeNode* root,long long low,long long high){
        if(!root)
            return true;
        if(root->val>=high||root->val<=low)
            return false;
        return search(root->left,low,root->val)&&search(root->right,root->val,high);
    }
    bool isValidBST(TreeNode* root) {
        return search(root,LONG_MIN,LONG_MAX);
    }
};

 617. Merge binary tree

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1==nullptr)  return root2;
        if(root2==nullptr)  return root1;
        TreeNode* merged=new TreeNode(root1->val+root2->val);
        merged->left=mergeTrees(root1->left,root2->left);
        merged->right=mergeTrees(root1->right,root2->right);
        return merged;
    }
};

 114. Expand the binary tree into a linked list

class Solution {
public:
    void flatten(TreeNode* root) {
        vector<TreeNode*>l;
        preorderTraversal(root,l);
        int size=l.size();
        for(int i=1;i<size;i++)
        {
            TreeNode *pre=l[i-1],*cur=l[i];
            pre->left=nullptr;
            pre->right=cur;
        }
    }
    void preorderTraversal(TreeNode* root,vector<TreeNode*> &l) {
        if(!root)
            return;
        l.push_back(root);
        preorderTraversal(root->left,l);
        preorderTraversal(root->right,l);
    }
};

105. Construct binary tree from preorder and inorder traversal sequences

class Solution {
public:
    TreeNode* myTree(const unordered_map<int,int>& hashmap,vector<int>& preorder, vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if(preorder_left>preorder_right) return nullptr;
        int preorder_root=preorder[preorder_left];
        int pIndex=hashmap.at(preorder_root);
        TreeNode* root=new TreeNode(preorder_root);
        int left_size=pIndex-inorder_left;
        root->left=myTree(hashmap,preorder,inorder,preorder_left+1,preorder_left+left_size,inorder_left,pIndex-1);
        root->right=myTree(hashmap,preorder,inorder,preorder_left+left_size+1,preorder_right,pIndex+1,inorder_right);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        unordered_map<int,int> hashmap;
        for(int i=0;i<inorder.size();i++){
            hashmap[inorder[i]]=i;
        }
        return myTree(hashmap,preorder,inorder,0,preorder.size()-1,0,inorder.size()-1);
    }
};