catalogue
1. Check whether the two trees are the same
2. Judge whether a tree is a subtree of another tree
3. Judge whether a tree is a balanced binary tree
5.2 sequence traversal returns the nodes of each layer
6.1 nearest common ancestor of binary tree
6.2 find the nearest common ancestor method 2 find the intersection of the linked list:
7. Input a binary search tree and convert the binary search tree into a sorted two-way linked list
8. Construct binary tree through preorder traversal and inorder traversal
9. The binary tree is constructed by post order traversal and middle order traversal
10. Construction and traversal of binary tree
11. Non recursive preorder traversal
12. Sequence traversal in non recursive implementation
13. Non recursive post order traversal
1. Check whether the two trees are the same
public boolean isSameTree(TreeNode p,TreeNode q){
if((p == null && q != null) || (p != null && q == null)){
return false;
}
if(p == null && q == null){
return true;
}
if(p.val != q.val){
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}2. Judge whether a tree is a subtree of another tree
public boolean isSameTree(TreeNode p, TreeNode q) {
if ((p == null && q != null) || (p != null && q == null)) {
return false;
}
if (p == null && q == null) {
return true;
}
if (p.val != q.val) {
return false;
}
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
public boolean isSubTree(TreeNode root, TreeNode subRoot) {
if (root == null || subRoot == null) {
return false;
}
if (isSameTree(root, subRoot)) {
return true;
}
if (isSameTree(root.left, subRoot)) {
return true;
}
if (isSameTree(root.right, subRoot)) {
return true;
}
return false;
}
3. Judge whether a tree is a balanced binary tree
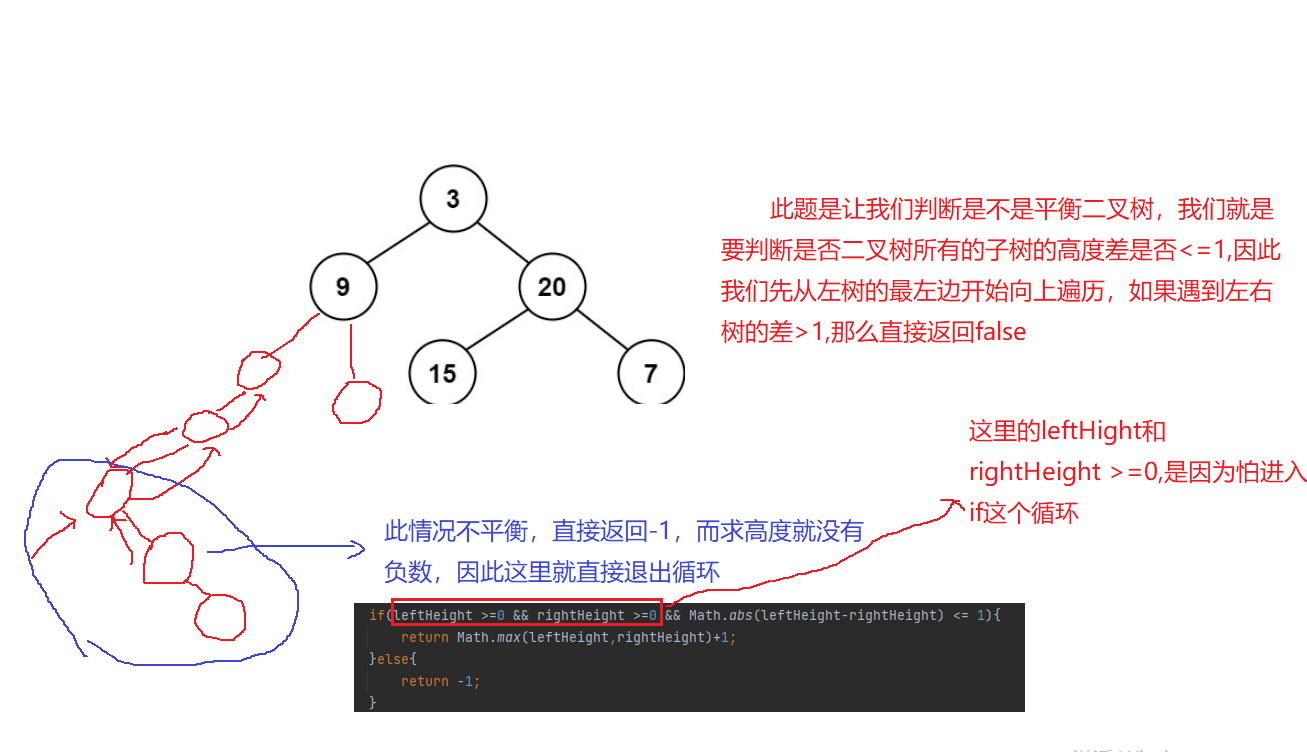
public int height(TreeNode root){
if(root == null){
return 0;
}
int leftHeight = height(root.left);
int rightHeight = height(root.right);
if(leftHeight >=0 && rightHeight >=0 && Math.abs(leftHeight-rightHeight) <= 1){
return Math.max(leftHeight,rightHeight)+1;
}else{
return -1;
}
}
public boolean isBalanced(TreeNode root){
if(root == null){
return true;
}
return height(root) > 0;
}4. Symmetric binary tree
public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){
if((leftTree == null && rightTree != null)||(leftTree != null && rightTree == null)){
return false;
}
//Empty nodes are also symmetrical
if(leftTree == null && rightTree == null){
return true;
}
if(leftTree.val != rightTree.val){
return false;
}
return isSymmetricChild(leftTree.left,rightTree.right) && isSymmetricChild(leftTree.right,rightTree.left);
}
//Symmetric binary tree
public boolean isSymmetric(TreeNode root){
if(root == null){
return true;
}
return isSymmetricChild(root.left,root.right);
}5.1 sequence traversal
public void levelOrder1(TreeNode root){
Queue<TreeNode> queue = new LinkedList<>();
if(root == null){
return;
}
queue.offer(root);
while (! queue.isEmpty()){
TreeNode cur = queue.poll();
System.out.println(cur.val+" ");
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
}5.2 sequence traversal returns the nodes of each layer
public List<List<Integer>> levelOrder2(TreeNode root){
List<List<Integer>> ret = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
if(root == null){
return ret;
}
queue.offer(root);
while (! queue.isEmpty()){
int size = queue.size();
List<Integer> list = new ArrayList<>();
while (size != 0){
TreeNode cur = queue.poll();
list.add(cur.val);
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
size--;
}
ret.add(list);,//After the nodes of each layer are completed, they are placed in the list
}
return ret;
}6.1 nearest common ancestor of binary tree
Method 1:

//Find common ancestor method 1 and treat it as a binary search tree
public TreeNode lowestCommonAncestor1(TreeNode root,TreeNode p,TreeNode q){
if(root == null){
return null;
}
if(root == p || root == q){
return root;
}
TreeNode leftT = lowestCommonAncestor1(root.left,p,q);
TreeNode rightT = lowestCommonAncestor1(root.right,p,q);
if(leftT != null && rightT != null){
return root;
}else if(leftT != null){
return leftT;
}else {
return rightT;
}
}6.2 find the nearest common ancestor method 2 find the intersection of the linked list:
//Root: root node: specified node stack: store the path from the root node to the specified node
public boolean getPath(TreeNode root,TreeNode node,Stack<TreeNode> stack){
if(root == null || node == null){
return false;
}
stack.push(root);
if(root == node){
return true;
}
boolean flg = getPath(root.left,node,stack);
if(flg == true){
return true;
}
flg = getPath(root.right,node,stack);
if(flg == true){
return true;
}
stack.pop();
return false;
}
public TreeNode lowestCommonAncestor2(TreeNode root,TreeNode p,TreeNode q){
if(root == null){
return null;
}
Stack<TreeNode> stack1 = new Stack<>();
getPath(root,p,stack1);
Stack<TreeNode> stack2 = new Stack<>();
getPath(root,p,stack2);
int size1 = stack1.size();
int size2 = stack2.size();
if(size1 > size2){
int size = size1 - size2;
while (size != 0){
stack1.pop();
size--;
}
while (!stack1.isEmpty() && !stack2.isEmpty()){
//Determine the addresses of two
if(stack1.peek() == stack2.peek()){
return stack1.pop();
}else {
stack1.pop();
stack2.pop();
}
}
}else{
int size = size2 - size1;
while (size != 0){
stack2.pop();
size--;
}
while (!stack1.isEmpty() && !stack2.isEmpty()){
//Determine whether the addresses of two are the same
if(stack1.peek() == stack2.peek()){
return stack1.pop();
}else {
stack1.pop();
stack2.pop();
}
}
}
return null;
}
7. Input a binary search tree and convert the binary search tree into a sorted two-way linked list

//Enter a binary search tree and convert the binary search tree into a sorted two-way linked list
//Middle order traversal
TreeNode prev = null;
public void inorder(TreeNode pCur){
if(pCur == null){
return;
}
inOrder(pCur.left);
pCur.left = prev;
if(prev != null){
prev.right = pCur;
}
prev = pCur;
//Print
//System.out.println(pCur.val+" ");
inorder(pCur.right);
}
public TreeNode Convert(TreeNode pRootOfTree){
if(pRootOfTree == null){
return null;
}
inorder(pRootOfTree);
TreeNode head = pRootOfTree;
while (head.left != null){
head = head.left;
}
return head;
}8. Construct binary tree through preorder traversal and inorder traversal
Note: the following preIndex should be written on the outside to prevent the end of the cycle. After going back, you can't remember the current position

//The binary tree is constructed by preorder traversal and inorder traversal
public int preIndex = 0;
public TreeNode createTreeByPandI(int[] preorder,int[] inorder,int inbegin,int inend ){
//Recursive termination condition. If this condition is met, there is no left tree or right tree
if(inbegin > inend){
return null;
}
TreeNode root = new TreeNode(preorder[preIndex]);//Before construction, traverse the first node
int rootIndex = findIndexOfI(inorder,inbegin,inend,preorder[preIndex]);//Find the location of the root node in the middle order traversal
if(rootIndex == -1){
return null;
}
preIndex++;
root.left = createTreeByPandI(preorder,inorder,inbegin,rootIndex-1);
root.right = createTreeByPandI(preorder,inorder,rootIndex+1,inend);
return root;
}
private int findIndexOfI(int[] inorder,int inbegin,int inend,int key){
for (int i = inbegin; i <=inend ; i++) {
if(inorder[i] == key){
return i;
}
}
return -1;
}
public TreeNode buildTree(int[] preorder,int[] inorder){
if(preorder == null || inorder == null){
return null;
}
return createTreeByPandI(preorder,inorder,0,inorder.length-1);
}9. The binary tree is constructed by post order traversal and middle order traversal
Similar to the above, it only needs simple modification:
//The binary tree is constructed according to post order traversal and middle order traversal
public int postIndex = 0;
public TreeNode createTreeByPandI(int[] inorder, int[] postorder,int inbegin,int inend){
if(inbegin > inend){
return null;
}
//Define the first node in the preorder traversal
TreeNode root = new TreeNode(postorder[postIndex]);
//Find the location of the root node in the middle order traversal
int rootIndex = findIndex(inorder,inbegin,inend,postorder[postIndex]);
if(rootIndex == -1){
return null;
}
postIndex--;
//Traverse the right, then the left
root.right = createTreeByPandI(inorder,postorder,rootIndex+1,inend);
root.left = createTreeByPandI(inorder,postorder,inbegin,rootIndex-1);
return root;
}
public int findIndex(int[] inorder,int begin,int inend,int key){
for(int i = begin;i <= inend;i++){
if(inorder[i] == key){
return i;
}
}
return -1;
}
public TreeNode buildTree(int[] postorder, int[] inorder) {
if(postorder == null || inorder == null){
return null;
}
postIndex = inorder.length-1;
return createTreeByPandI(postorder,inorder,0,inorder.length-1);
}
}10. Construction and traversal of binary tree
import java.util.*;
//Build node
class TreeNode{
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val){
this.val = val;
}
}
public class Main{
public static int i =0;
public static TreeNode createNode(String str){
//Create a new root node, root, because you have to create a new node every time you come back. So leave it empty
TreeNode root = null;
if(str.charAt(i) != '#'){
root = new TreeNode(str.charAt(i));
i++;
root.left = createNode(str);
root.right = createNode(str);
}else{
i++;
}
return root;
}
//Middle order traversal
public static void inOrder(TreeNode root){
if(root == null){
return;
}
inOrder(root.left);
System.out.print(root.val+" ");
inOrder(root.right);
}
public static void main(String[] arg){
Scanner in = new Scanner(System.in);
//hasNextLine does not end when it encounters a space
//hasNext ends when a space is encountered
while(in.hasNextLine()){
String str = in.nextLine();
TreeNode root = createNode(str);
inOrder(root);
}
}
}11. Non recursive preorder traversal
void preOrderNor(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
System.out.print(cur.val + " ");
cur = cur.left;
}
TreeNode top = stack.pop();
cur = top.right;
}
}12. Sequence traversal in non recursive implementation
void inOrderNor(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.pop();
System.out.print(top.val+" ");
cur = top.right;
}
}13. Non recursive post order traversal

public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ret = new ArrayList();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode prev = null;
while(cur != null || !stack.isEmpty()){
while(cur != null){
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.peek();
if(top.right == null || top.right == prev){
stack.pop();
ret.add(top.val);
prev = top;//Point to the pop-up node
}else{
cur = top.right;
}
}
return ret;
}