Differential constraint system
What is differential constraint system
Difference constraint system refers to a method to solve the following multivariate primary inequality system, in which (y1,y2... yn are constants), which is called difference because each inequality of multivariate primary inequality system is about the difference between two independent variables
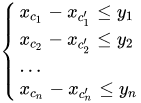
There are two general questions:
- Find a set of solutions of (x1,x2,... xn) that meet the conditions
- Find the maximum or minimum value of a certain X or some x that meet the conditions
Find a set of solutions of (x1,x2,... xn) that meet the conditions
For this inequality group, we can find that it is either no solution or infinite solution, because if there is a group of solutions that satisfy the inequality group, adding or subtracting the same number from all x will certainly satisfy the inequality group
Q: How to solve it?
Here we take an inequality to see: x i − x j < = c x_i-x_j<=c xi−xj<=c
For item shifting simplification: x i < = x j + c x_i<=x_j+c xi<=xj+c
It can be found that this form is similar to the shortest path relaxation operation. It is written in the form of inequality: d i s [ i ] < = d i s [ j ] + c dis[i]<=dis[j]+c Dis [i] < = dis [j] + c is equivalent to establishing an edge with a weight of c between j and I, which will be satisfied after finding the shortest circuit d i s [ i ] < = d i s [ j ] + c dis[i]<=dis[j]+c Dis [i] < = dis [J] + C, because it is the basic property of the shortest path problem, we can build all inequalities into a graph by connecting edges, and run a single source shortest path on this graph
Q: Single source is the shortest. Who is the source?
In order to ensure that all inequalities are satisfied, that is, all edges must be traversed, we need to establish a super source point 0 or n+1 as the source point, and he must connect an edge with a weight of 0 with all points, that is, dis [i] < = dis[0] + 0. Point 0 is not the required point, so no matter what the value of dis[0] is, In the case of no solution, there is still no solution. As we mentioned above, it doesn't matter to change the relative size. Generally speaking, we will make dis[0] = 0. If the size of the problem to be solved is greater than or equal to 0, we just need to take the minimum value from 1 to n and subtract the minimum value from the values of all points
Q: When is there no solution?
Let's start with the conclusion: the presence of a negative ring represents no solution
Let's prove:
Suppose there is a heap condition as follows:
x
1
<
=
x
2
+
c
1
x
2
<
=
x
3
+
c
2
.
.
.
x
n
<
=
x
1
+
c
n
x1<=x2+c1\\ x2<=x3+c2\\ ...\\ xn<=x1+cn
x1<=x2+c1x2<=x3+c2...xn<=x1+cn
By scaling the inequality, we can get:
x
1
<
=
x
1
+
∑
i
=
1
n
c
i
Namely
∑
i
=
1
n
c
i
>
=
0
x1<=x1+ \sum_ {I = 1} ^ {n}{c_i} \ \ i.e. \ sum_ {i=1}^{n}{c_i}>=0
X1 < = X1 + i=1 Σ n ci, i=1 Σ n ci > = 0
This is a condition we get from the inequality. Obviously, the inequality I wrote is a ring, and the sum of the weights of the ring is
∑
i
=
1
n
c
i
\sum_{i=1}^{n}{c_i}
Σ i=1n ci, if there is a negative ring, it does not meet the condition, and there is no solution
Q: Problem solving steps?
- Convert the input conditions to form, such as x v < = x u + c x_v<=x_u+c xv < = Xu + c, and then build an edge with the weight of c from u to v
- Take a super source point 0 and build an edge with i weight 0 from 0, 1 < = i < = n
- Run SPFA, if there is a negative loop, it means there is no solution, otherwise output dis[i]
Let's take a board question and see how the code is written
P5960 [template] differential constraint algorithm
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 1000000007
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
typedef long long ll;
typedef pair <int,int> pii;
#define MAX 300000 + 50
int n, m;
int a, b, c;
int tot;
int head[MAX];
struct ran{
int to, nex, val;
}tr[MAX];
inline void add(int u, int v, int c){
tr[++tot].to = v;
tr[tot].val = c;
tr[tot].nex = head[u];
head[u] = tot;
}
bool vis[MAX];
int dis[MAX];
int cnt[MAX];
void SPFA(){
queue<int>q;
for(int i = 1; i <= n; ++i){
vis[i] = 1;
q.push(i);
}
while (!q.empty()) {
int u = q.front();q.pop();vis[u] = 0;
for(int i = head[u]; i; i = tr[i].nex){
int v = tr[i].to;
if(dis[v] > dis[u] + tr[i].val){
dis[v] = dis[u] + tr[i].val;
cnt[v] = cnt[u] + 1;
if(cnt[v] >= n){//Negative ring
cout << "NO" << endl;
return;
}
if(!vis[v]){
vis[v] = 1;
q.push(v);
}
}
}
}
for(int i = 1; i <= n; ++i)cout << dis[i] << ' ';
cout << endl;
}
void work(){
cin >> n >> m;
while (m--) {
cin >> a >> b >> c;
add(b, a, c);
}
SPFA();
}
int main(){
io;
work();
return 0;
}
Find the maximum or minimum value of a certain X or some x that meet the conditions
Generally speaking, the first case is relatively simple and board, so on this basis, there will be some restrictions. For example, when dis[0] = w has an unknown number, after establishing the super source point, you will get x 1 , x 2 , . . . , x n < = w x_1,x_2,...,x_n<=w x1,x2,..., A set of solutions of xn < = w, with the limitation of this condition, can be obtained by running the shortest path x 1 , x 2 , . . . , x n < = w x_1,x_2,...,x_n<=w x1,x2,..., The maximum value of the solution under the condition of xn < = W.
The certificate is as follows:
for instance:
x
1
<
=
x
2
+
2
x
1
<
=
x
2
+
3
x
1
<
=
x
2
+
4
x
2
=
0
x_1<=x_2+2\\ x_1<=x_2 + 3\\ x_1<=x_2 + 4\\ x2 = 0
x1<=x2+2x1<=x2+3x1<=x2+4x2=0
The result of the shortest run is
x
1
<
=
2
x_1<=2
x1 < = 2, which is obviously
x
1
x_1
The maximum value of x1. X1 can only take a value less than or equal to 2, which is the maximum value
Q: What about the minimum?
We only need to shift the inequality to construct the case of > = to run the longest road once
x
1
<
=
x
2
+
c
1
turn
change
by
x
2
>
=
x
1
−
c
1
x
2
<
=
x
3
+
c
2
turn
turn
by
x
3
>
=
x
2
−
c
2
.
.
.
x
n
<
=
x
1
+
c
n
turn
change
become
x
1
>
=
x
n
−
c
n
x_ 1<=x_ 2+c_ 1 to X_ 2>=x_ 1-c_ 1\ x_ 2<=x_ 3+c_ 2 to X_ 3>=x_ 2-c_ 2\ ...\ x_ n<=x_ 1+c_ Convert n to X_ 1>=x_ n-c_ n
X1 < = x2 + c1 to x2 > = x1 − c1 x2 < = x3 + c2 to x3 > = x2 − c2 Xn < = X1 + CN converted to X1 > = xn − cn
x v > = x u − c x_v>=x_u-c xv > = Xu − c can be converted into an edge with a weight of - c from u to v in the longest path
Just run the longest way. If there is a positive ring, there is no solution
Q: How to solve the problem:
-
The first question is whether to find the minimum value or the maximum value
-
If it is to find the minimum value, it means to run the longest road, and we construct the inequality of > =
If it is to find the maximum value, it means that it is to run the shortest path, and we construct the inequality of < =
-
Then establish the super source point, run the shortest or longest way, and pay attention to the situation without solution
P6145 [USACO20FEB]Timeline G
Title Description:
Milking was carried out n times in m days, and the i milking was not earlier than Si days. In addition, there are c requirements (a, b, x), which means that the b milking is at least X days after the end of the a milking
What is the earliest date of each milking
Idea:
First of all, to see the earliest date is to find the minimum value, which is to run the longest road, so we need to establish the inequality of > =
The first condition is converted to inequality: d i s [ i ] > = S i dis[i]>= S_i dis[i]>=Si
The second condition is converted to inequality: d i s [ b ] > = d i s [ a ] + x dis[b] >= dis[a] + x dis[b]>=dis[a]+x
We can create a super source point 0,dis[0] = 0, so that the first condition can be converted into d i s [ i ] > = d i s [ 0 ] + S i dis[i] >= dis[0]+S_i Dis [i] > = dis [0] + Si, it can be seen that an edge with the weight of Si is established from 0 to I. the second condition can be seen that an edge with the weight of x is established from a to b, and then run the longest road
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define inf 0x3f3f3f3f
#define mod 1000000007
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
typedef long long ll;
typedef pair <int,int> pii;
#define MAX 300000 + 50
int n, m, k, s;
int a, b, c;
int tot;
int head[MAX];
struct ran{
int to, nex, val;
}tr[MAX];
inline void add(int u, int v, int c){
tr[++tot].to = v;
tr[tot].val = c;
tr[tot].nex = head[u];
head[u] = tot;
}
ll dis[MAX];
bool vis[MAX];
void SPFA(){
queue<int>q;
mem(dis, -inf);
q.push(0);dis[0] = 0;vis[0] = 1;
while (!q.empty()) {
int u = q.front();q.pop();vis[u] = 0;
for(int i = head[u]; i; i = tr[i].nex){
int v = tr[i].to;
if(dis[v] < dis[u] + tr[i].val){
dis[v] = dis[u] + tr[i].val;
if(!vis[v]){
q.push(v);
vis[v] = 1;
}
}
}
}
for(int i = 1; i <= n; ++i)cout << dis[i] << endl;
}
void work(){
cin >> n >> m >> k;
for(int i = 1; i <= n; ++i){
cin >> s;
add(0, i, s);
}
while (k--) {
cin >> a >> b >> c;
add(a, b, c);
}
SPFA();
}
int main(){
io;
work();
return 0;
}
summary
-
It is difficult to check the map under construction with score constraints
-
Run the longest road when seeking the maximum value and convert it into the form of > =
When seeking the minimum value, run the shortest circuit and convert it into the form of < =
-
There is no solution if there is a negative loop when running the shortest circuit
There is no solution if there is a positive ring when running the longest road
-
Special drawing method:
Let a[i] be the value of the ith position, and find the prefix sum[i] = sum[i - 1] + a[i], which can realize the mapping of inequalities about interval weights. At this time, there is a most basic relationship: 0 < = s u m [ i ] − s u m [ i − 1 ] < = 1 0<=sum[i] - sum[i - 1]<=1 0 < = sum[i] − sum[i − 1] < = 1. Other relationships should be explored according to the topic
-
In the case of equal sign only, it should be noted that two-way edges should be established, such as: x 1 = x 2 + c x1=x2+c x1=x2+c, which should be converted into inequalities such as X1 < = x2 + C and X2 < = x1-c. whether to use the less than sign or the greater than sign depends on the subject requirements