preface
This note mainly introduces the function of autograd module in pytorch, mainly involves the code under torch/autograd, and does not involve the underlying C + + implementation. The source code involved in this article is subject to PyTorch 1.7.
- torch.autograd.function (back propagation of function)
- torch.autograd.functional (back propagation of computational graph)
- torch.autograd.gradcheck (numerical gradient check)
- torch.autograd.anomaly_mode (detect error generation path during automatic derivation)
- torch.autograd.grad_mode (set whether gradient is required)
- model.eval() and torch no_ grad()
- torch.autograd.profiler (provides function level statistics)
torch.autograd.function (back propagation of function)
When we build a network, we usually use NN provided by pytorch Module (such as nn.Conv2d, nn.ReLU, etc.) as the basic unit. These modules usually wrap the autograd function as part of the real implementation. For example, NN Relu actually uses torch nn. functional. relu(F.relu):
from torch.nn import functional as F
class ReLU(Module):
__constants__ = ['inplace']
inplace: bool
def __init__(self, inplace: bool = False):
super(ReLU, self).__init__()
self.inplace = inplace
def forward(self, input: Tensor) -> Tensor:
return F.relu(input, inplace=self.inplace)The F.relu type here is function. If another layer is stripped, the function type of the actual package is builtin_function_or_method, which is also the part that really completes the operation. These parts are usually implemented in C + + (such as ATen). So far, we know that the operation part of a model is composed of autograd functions. Forward and backward are defined in these autograd functions to describe the process of forward and gradient back transmission. After combination, the forward and gradient back transmission of the whole model can be realized. In torch autograd. The function class defined in function is the base class. We can implement the custom autograd function. The implemented function needs to include forward and backward methods. Take Exp and GradCoeff as examples to explain:
class Exp(Function): # Calculate e^x for this layer
@staticmethod
def forward(ctx, i): # Model forward
result = i.exp()
ctx.save_for_backward(result) # Save the required contents for backward use, and the required results will be saved in saved_tensors tuple; Only tensor type variables can be saved here. If other type variables (Int, etc.), ctx can be directly assigned as member variables, or the saving effect can be achieved
return result
@staticmethod
def backward(ctx, grad_output): # Model gradient back propagation
result, = ctx.saved_tensors # Take out the result saved in forward
return grad_output * result # Calculate gradient and return
# Try to use
x = torch.tensor([1.], requires_grad=True) # You need to set the requirements of the tensor_ Only when the grad property is True can gradient backpropagation be performed
ret = Exp.apply(x) # Use the apply method to call the custom autograd function
print(ret) # tensor([2.7183], grad_fn=<ExpBackward>)
ret.backward() # Reverse gradient
print(x.grad) # tensor([2.7183])The forward direction of exp function is very simple. You can directly call the member method exp of tensor. In reverse, we know

Therefore, we use it directly

Multiply by grad_ The gradient is output. We found that our custom function Exp performs forward and reverse correctly. At the same time, we also note that the results obtained from the front and back include grad_fn attribute, which points to the function used to calculate its gradient (i.e. the backward function of Exp). This will be explained in more detail in the next section. Next, let's look at another function, GradCoeff, whose function is to multiply the backscattering gradient by a user-defined coefficient.
class GradCoeff(Function):
@staticmethod
def forward(ctx, x, coeff): # Model forward
ctx.coeff = coeff # Save coeff as a member variable of ctx
return x.view_as(x)
@staticmethod
def backward(ctx, grad_output): # Model gradient back propagation
return ctx.coeff * grad_output, None # The number of outputs of backward should be the same as the number of inputs of forward. Here, coeff does not need gradient, so it returns None
# Try to use
x = torch.tensor([2.], requires_grad=True)
ret = GradCoeff.apply(x, -0.1) # The forward needs to provide both x and coeff, and set coeff to - 0.1
ret = ret ** 2
print(ret) # tensor([4.], grad_fn=<PowBackward0>)
ret.backward()
print(x.grad) # tensor([-0.4000]), the gradient has been multiplied by the corresponding coefficienttorch.autograd.functional (back propagation of computational graph)
In the previous section, we described the back propagation of a single function and how to write a custom autograd function. In this section, we briefly introduce the interface of computing graph back propagation provided in pytorch.
In the training process, we usually use prediction and groundtruth label to calculate loss (the type of loss is Tensor), and then call loss.. Backward() performs gradient backpropagation. The backward method of tensor class actually calls torch autograd. Backward interface. This python interface implements the back propagation of computational graph level.
class Tensor(torch._C._TensorBase)
def backward(self, gradient=None, retain_graph=None, create_graph=False):
relevant_args = (self,)
...
torch.autograd.backward(self, gradient, retain_graph, create_graph)
# gradient: the shape is consistent with tensor, which can be understood as the intermediate result of chain derivation. If tensor is scalar, it can be omitted (1 by default)
# retain_graph: gradient accumulation during multiple back propagation. The intermediate cache of back propagation will be emptied. To perform multiple back propagation, you need to specify retain_graph=True to save these caches.
# create_graph: a calculation diagram is also established for the process of back propagation, which can be used to calculate the second-order derivativeIn the implementation of pytorch, autograd will record all operations that generate the current variable with the user's operation, and establish a directed acyclic graph (DAG). The operation Function is recorded in the figure, and the position of each variable in the figure can be determined by its grad_ The position of FN attribute in the figure is inferred. In the process of back propagation, autograd traces the source from the current variable (root node F) along this graph, and the gradient of all leaf nodes can be calculated by using the chain derivation rule. Each Function of forward propagation operation has its corresponding back propagation Function to calculate the gradient of each input variable. The Function name of these functions usually ends with Backward. We construct a simplified calculation diagram and take it as an example for a brief introduction.
A = torch.tensor(2., requires_grad=True) B = torch.tensor(.5, requires_grad=True) E = torch.tensor(1., requires_grad=True) C = A * B D = C.exp() F = D + E print(F) # Tensor (3.7183, grad_fn = < AddBackward0 >) prints the calculation results, and you can see the grad of F_ FN points to AddBackward, that is, the operation that generates F print([x.is_leaf for x in [A, B, C, D, E, F]]) # [True, True, False, False, True, False] print whether it is a leaf node, created by the user, and requires_ Nodes with grad set to True are leaf nodes print([x.grad_fn for x in [F, D, C, A]]) # [< addbackward0 object at 0x7f972de8c7b8 >, < expbackward0 object at 0x7f972de8c278 >, < mulbackward0 object at 0x7f972de8c2b0 >, none] grad of each variable_ FN points to the backward function that generates its operator and grad of leaf node_ FN is empty print(F.grad_fn.next_functions) # ((< expiated object at 0x7f972de8c390 >, 0), (< AccumulateGrad object at 0x7f972de8c5f8 >, 0)) since F = D + E, F.grad_fn.next_functions also has two terms, corresponding to D and e variables respectively. The first term in each tuple corresponds to grad of the corresponding variable_ FN, the second item indicates that the corresponding variable is the output that produces its op. E is a leaf node without grad_fn, but there is a gradient accumulation function, i.e. AccumulateGrad (because there are many gradients during reverse transmission, it needs to be accumulated) F.backward(retain_graph=True) # Carry out gradient reverse transmission print(A.grad, B.grad, E.grad) # tensor(1.3591) tensor(5.4366) tensor(1.) The gradient of each variable is calculated, which is consistent with that obtained by derivation print(C.grad, D.grad) # None None to save space, the gradient of the intermediate node will not be retained after the gradient reverse transmission is completed
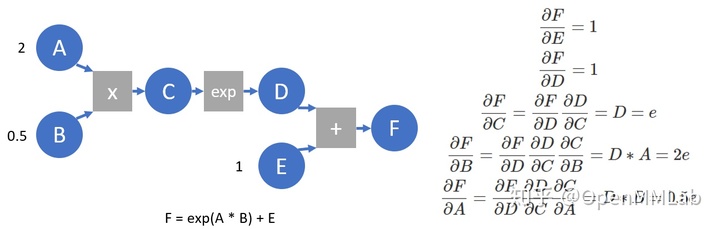
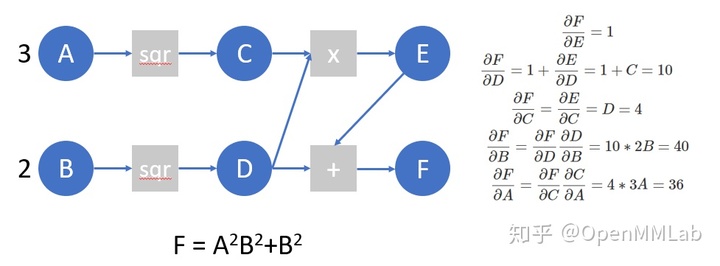
Let's take another look at the following calculation diagram and simulate the work done by autograd on this calculation diagram:
A = torch.tensor([3.], requires_grad=True) B = torch.tensor([2.], requires_grad=True) C = A ** 2 D = B ** 2 E = C * D F = D + E F.manual_grad = torch.tensor(1) # We use manual_grad indicates that when the structure of the calculation graph is known, we simulate the gradient calculated manually by the autograd process D.manual_grad, E.manual_grad = F.grad_fn(F.manual_grad) C.manual_grad, tmp2 = E.grad_fn(E.manual_grad) D.manual_grad = D.manual_grad + tmp2 # Here, we first complete the gradient accumulation on D, and then reverse transmission A.manual_grad = C.grad_fn(C.manual_grad) B.manual_grad = D.grad_fn(D.manual_grad) # (tensor([24.], grad_fn=<MulBackward0>), tensor([40.], grad_fn=<MulBackward0>))
Next, we write a simple function, perform autograd on this calculation diagram, and verify whether the result is correct:
# This example can only be used when each op produces only one output, and the efficiency is very low (because for a node, the gradient returned this time is directly transmitted to the leaf node without waiting for all gradients to be transmitted back to this node each time)
def autograd(grad_fn, gradient):
auto_grad = {}
queue = [[grad_fn, gradient]]
while queue != []:
item = queue.pop()
gradients = item[0](item[1])
functions = [x[0] for x in item[0].next_functions]
if type(gradients) is not tuple:
gradients = (gradients, )
for grad, func in zip(gradients, functions):
if type(func).__name__ == 'AccumulateGrad':
if hasattr(func.variable, 'auto_grad'):
func.variable.auto_grad = func.variable.auto_grad + grad
else:
func.variable.auto_grad = grad
else:
queue.append([func, grad])
A = torch.tensor([3.], requires_grad=True)
B = torch.tensor([2.], requires_grad=True)
C = A ** 2
D = B ** 2
E = C * D
F = D + E
autograd(F.grad_fn, torch.tensor(1))
print(A.auto_grad, B.auto_grad) # tensor(24., grad_fn=<UnbindBackward>) tensor(40., grad_fn=<AddBackward0>)
# This autograd can also act on the model written. We will see that it produces the same results as the backward provided by pytorch
from torch import nn
class MLP(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(10, 5)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(5, 2)
self.fc3 = nn.Linear(5, 2)
self.fc4 = nn.Linear(2, 2)
def forward(self, x):
x = self.fc1(x)
x = self.relu(x)
x1 = self.fc2(x)
x2 = self.fc3(x)
x2 = self.relu(x2)
x2 = self.fc4(x2)
return x1 + x2
x = torch.ones([10], requires_grad=True)
mlp = MLP()
mlp_state_dict = mlp.state_dict()
# Customize autograd
mlp = MLP()
mlp.load_state_dict(mlp_state_dict)
y = mlp(x)
z = torch.sum(y)
autograd(z.grad_fn, torch.tensor(1.))
print(x.auto_grad) # tensor([-0.0121, 0.0055, -0.0756, -0.0747, 0.0134, 0.0867, -0.0546, 0.1121, -0.0934, -0.1046], grad_fn=<AddBackward0>)
mlp = MLP()
mlp.load_state_dict(mlp_state_dict)
y = mlp(x)
z = torch.sum(y)
z.backward()
print(x.grad) # tensor([-0.0121, 0.0055, -0.0756, -0.0747, 0.0134, 0.0867, -0.0546, 0.1121, -0.0934, -0.1046])python uses dynamic graph, and its calculation graph is built from scratch every time forward propagation, so it can use python control statements (such as for, if, etc.) to create calculation graph according to requirements. Here is an example:
def f(x):
result = 1
for ii in x:
if ii.item()>0: result=ii*result
return result
x = torch.tensor([0.3071, 1.1043, 1.3605, -0.3471], requires_grad=True)
y = f(x) # y = x[0]*x[1]*x[2]
y.backward()
print(x.grad) # tensor([1.5023, 0.4178, 0.3391, 0.0000])
x = torch.tensor([ 1.2817, 1.7840, -1.7033, 0.1302], requires_grad=True)
y = f(x) # y = x[0]*x[1]*x[3]
y.backward()
print(x.grad) # tensor([0.2323, 0.1669, 0.0000, 2.2866])The previous example used tensor Backward () interface (call autograd.backward internally). Let's introduce the jacobian() and hessian() interfaces provided by autograd and use them directly for automatic differentiation. The inputs of these two functions are the operation function (accept the input tensor and return the output tensor) and the input tensor, which returns the jacobian and hessian matrices. For the jacobian interface, the input and output can be n-dimensional tensors. For the hessian interface, the output must be a scalar. The tensor shape returned by jacobian is output_dim x input_dim (if the function output is scalar, output_dim can be omitted), and the tensor returned by hessian is input_dim x input_dim. In addition, the two automatic differential interfaces support the operation function to receive and output multiple tensors at the same time.
from torch.autograd.functional import jacobian, hessian
from torch.nn import Linear, AvgPool2d
fc = Linear(4, 2)
pool = AvgPool2d(kernel_size=2)
def scalar_func(x):
y = x ** 2
z = torch.sum(y)
return z
def vector_func(x):
y = fc(x)
return y
def mat_func(x):
x = x.reshape((1, 1,) + x.shape)
x = pool(x)
x = x.reshape(x.shape[2:])
return x ** 2
vector_input = torch.randn(4, requires_grad=True)
mat_input = torch.randn((4, 4), requires_grad=True)
j = jacobian(scalar_func, vector_input)
assert j.shape == (4, )
assert torch.all(jacobian(scalar_func, vector_input) == 2 * vector_input)
h = hessian(scalar_func, vector_input)
assert h.shape == (4, 4)
assert torch.all(hessian(scalar_func, vector_input) == 2 * torch.eye(4))
j = jacobian(vector_func, vector_input)
assert j.shape == (2, 4)
assert torch.all(j == fc.weight)
j = jacobian(mat_func, mat_input)
assert j.shape == (2, 2, 4, 4)In the previous example, we have introduced autograd Backward() saves only the gradient of leaf nodes in order to save space. If we want to know the gradient of the output about an intermediate result, we can choose to use autograd Grad () interface or hook mechanism:
A = torch.tensor(2., requires_grad=True)
B = torch.tensor(.5, requires_grad=True)
C = A * B
D = C.exp()
torch.autograd.grad(D, (C, A)) # (tensor(2.7183), tensor(1.3591)), the returned gradient is tuple type, and the grad interface supports gradient calculation for multiple variables
def variable_hook(grad): # hook is registered on tensor, and the input is the gradient transmitted back to this tensor
print('the gradient of C is: ', grad)
A = torch.tensor(2., requires_grad=True)
B = torch.tensor(.5, requires_grad=True)
C = A * B
hook_handle = C.register_hook(variable_hook) # Register hook on intermediate variable C
D = C.exp()
D.backward() # Printing during reverse transmission: the gradient of C is: tensor(2.7183)
hook_handle.remove() # If it is no longer needed, you can remove this hooktorch.autograd.gradcheck (numerical gradient check)
After writing your own autograd function, you can use the gradcheck and grad gradgradcheck interfaces provided in gradcheck to compare the gradient calculated by numerical value with the gradient calculated by derivation, so as to check whether the backward is written correctly. With function

As an example, it is obtained by numerical method

The gradient of the point is:

. In the following example, we implement the Sigmoid function ourselves and use gradcheck to check whether the backward is written correctly.
class Sigmoid(Function):
@staticmethod
def forward(ctx, x):
output = 1 / (1 + torch.exp(-x))
ctx.save_for_backward(output)
return output
@staticmethod
def backward(ctx, grad_output):
output, = ctx.saved_tensors
grad_x = output * (1 - output) * grad_output
return grad_x
test_input = torch.randn(4, requires_grad=True) # tensor([-0.4646, -0.4403, 1.2525, -0.5953], requires_grad=True)
torch.autograd.gradcheck(Sigmoid.apply, (test_input,), eps=1e-3) # pass
torch.autograd.gradcheck(torch.sigmoid, (test_input,), eps=1e-3) # pass
torch.autograd.gradcheck(Sigmoid.apply, (test_input,), eps=1e-4) # fail
torch.autograd.gradcheck(torch.sigmoid, (test_input,), eps=1e-4) # failWe found that when eps is 1e-3, both the Sigmoid we wrote and the builtin Sigmoid built in torch can pass the gradient check, but when eps drops to 1e-4, neither can pass. Under the general intuition, when calculating the numerical gradient, the smaller the eps, the value obtained should be closer to the real gradient. The abnormal phenomenon here is caused by the error caused by the accuracy of the machine: test_ The type of input is torch Float32, therefore, when the eps is too small, there is a large accuracy error (eps is taken as the divisor when calculating the numerical gradient), so there is a large gap between the eps and the real accuracy. Will test_ After the input is changed to the tensor of float64, this phenomenon no longer occurs. This also reminds us that when writing backward, we should consider some properties of numerical calculation and retain more accurate results as far as possible.
test_input = torch.randn(4, requires_grad=True, dtype=torch.float64) # tensor([-0.4646, -0.4403, 1.2525, -0.5953], dtype=torch.float64, requires_grad=True) torch.autograd.gradcheck(Sigmoid.apply, (test_input,), eps=1e-4) # pass torch.autograd.gradcheck(torch.sigmoid, (test_input,), eps=1e-4) # pass torch.autograd.gradcheck(Sigmoid.apply, (test_input,), eps=1e-6) # pass torch.autograd.gradcheck(torch.sigmoid, (test_input,), eps=1e-6) # pass
torch.autograd.anomaly_mode (detect error generation path during automatic derivation)
It can be used to detect the error generation path during automatic derivation with the help of with autograd detect_ Anomaly (): or torch autograd. set_ detect_ Anomaly (true) to enable:
>>> import torch
>>> from torch import autograd
>>>
>>> class MyFunc(autograd.Function):
...
... @staticmethod
... def forward(ctx, inp):
... return inp.clone()
...
... @staticmethod
... def backward(ctx, gO):
... # Error during the backward pass
... raise RuntimeError("Some error in backward")
... return gO.clone()
>>>
>>> def run_fn(a):
... out = MyFunc.apply(a)
... return out.sum()
>>>
>>> inp = torch.rand(10, 10, requires_grad=True)
>>> out = run_fn(inp)
>>> out.backward()
Traceback (most recent call last):
Some Error Log
RuntimeError: Some error in backward
>>> with autograd.detect_anomaly():
... inp = torch.rand(10, 10, requires_grad=True)
... out = run_fn(inp)
... out.backward()
Traceback of forward call that caused the error: # Trace where the error occurred was detected
File "tmp.py", line 53, in <module>
out = run_fn(inp)
File "tmp.py", line 44, in run_fn
out = MyFunc.apply(a)
Traceback (most recent call last):
Some Error Log
RuntimeError: Some error in backwardtorch.autograd.grad_mode (set whether gradient is required)
In the process of information, we don't want autograd to derive tensor, because it needs to cache many intermediate structures and increase additional memory / video memory overhead. In information, turning off automatic derivation can improve the speed to a certain extent and save a lot of memory and video memory (the saved part is not limited to the part originally used for gradient storage). We can use grad_ Troch in mode no_ Grad() to turn off automatic derivation:
from torchvision.models import resnet50
import torch
net = resnet50().cuda(0)
num = 128
inp = torch.ones([num, 3, 224, 224]).cuda(0)
net(inp) # If torch is not turned on no_ grad(),batch_ When the size is 128, it will OOM (on 1080 Ti)
net = resnet50().cuda(1)
num = 512
inp = torch.ones([num, 3, 224, 224]).cuda(1)
with torch.no_grad(): # Open torch no_ Batch after grad()_ When the size is 512, you can still run information (save more than 4 times of video memory)
net(inp)model.eval() and torch no_ grad()
These two items are actually irrelevant. They need to be opened in the process of information: model Eval() enables BatchNorm, Dropout and other module s in the model to adopt eval mode to ensure the correctness of the information result, but it does not save video memory; torch.no_grad() declares that it does not calculate gradients, saving a lot of memory and video memory.
torch.autograd.profiler (provides function level statistics)
import torch
from torchvision.models import resnet18
x = torch.randn((1, 3, 224, 224), requires_grad=True)
model = resnet18()
with torch.autograd.profiler.profile() as prof:
for _ in range(100):
y = model(x)
y = torch.sum(y)
y.backward()
# NOTE: some columns were removed for brevity
print(prof.key_averages().table(sort_by="self_cpu_time_total"))The output includes CPU time, proportion, call times and other information (since a kernel may call other kernels, Self CPU refers to the time consumed by itself (excluding the time consumed by other kernels being called)):
--------------------------------------------- ------------ ------------ ------------ ------------ ------------ ------------
Name Self CPU % Self CPU CPU total % CPU total CPU time avg # of Calls
--------------------------------------------- ------------ ------------ ------------ ------------ ------------ ------------
aten::mkldnn_convolution_backward_input 18.69% 1.722s 18.88% 1.740s 870.001us 2000
aten::mkldnn_convolution 17.07% 1.573s 17.28% 1.593s 796.539us 2000
aten::mkldnn_convolution_backward_weights 16.96% 1.563s 17.21% 1.586s 792.996us 2000
aten::native_batch_norm 9.51% 876.994ms 15.06% 1.388s 694.049us 2000
aten::max_pool2d_with_indices 9.47% 872.695ms 9.48% 873.802ms 8.738ms 100
aten::select 7.00% 645.298ms 10.06% 926.831ms 7.356us 126000
aten::native_batch_norm_backward 6.67% 614.718ms 12.16% 1.121s 560.466us 2000
aten::as_strided 3.07% 282.885ms 3.07% 282.885ms 2.229us 126900
aten::add_ 2.85% 262.832ms 2.85% 262.832ms 37.350us 7037
aten::empty 1.23% 113.274ms 1.23% 113.274ms 4.089us 27700
aten::threshold_backward 1.10% 101.094ms 1.17% 107.383ms 63.166us 1700
aten::add 0.88% 81.476ms 0.99% 91.350ms 32.625us 2800
aten::max_pool2d_with_indices_backward 0.86% 79.174ms 1.02% 93.706ms 937.064us 100
aten::threshold_ 0.56% 51.678ms 0.56% 51.678ms 30.399us 1700
torch::autograd::AccumulateGrad 0.40% 36.909ms 2.81% 258.754ms 41.072us 6300
aten::empty_like 0.35% 32.532ms 0.63% 57.630ms 6.861us 8400
NativeBatchNormBackward 0.32% 29.572ms 12.48% 1.151s 575.252us 2000
aten::_convolution 0.31% 28.182ms 17.63% 1.625s 812.258us 2000
aten::mm 0.27% 24.983ms 0.32% 29.522ms 147.611us 200
aten::stride 0.27% 24.665ms 0.27% 24.665ms 0.583us 42300
aten::mkldnn_convolution_backward 0.22% 20.025ms 36.33% 3.348s 1.674ms 2000
MkldnnConvolutionBackward 0.21% 19.112ms 36.53% 3.367s 1.684ms 2000
aten::relu_ 0.20% 18.611ms 0.76% 70.289ms 41.346us 1700
aten::_batch_norm_impl_index 0.16% 14.298ms 15.32% 1.413s 706.254us 2000
aten::addmm 0.14% 12.684ms 0.15% 14.138ms 141.377us 100
aten::fill_ 0.14% 12.672ms 0.14% 12.672ms 21.120us 600
ReluBackward1 0.13% 11.845ms 1.29% 119.228ms 70.134us 1700
aten::as_strided_ 0.13% 11.674ms 0.13% 11.674ms 1.946us 6000
aten::div 0.11% 10.246ms 0.13% 12.288ms 122.876us 100
aten::batch_norm 0.10% 8.894ms 15.42% 1.421s 710.700us 2000
aten::convolution 0.08% 7.478ms 17.71% 1.632s 815.997us 2000
aten::sum 0.08% 7.066ms 0.10% 9.424ms 31.415us 300
aten::conv2d 0.07% 6.851ms 17.78% 1.639s 819.423us 2000
aten::contiguous 0.06% 5.597ms 0.06% 5.597ms 0.903us 6200
aten::copy_ 0.04% 3.759ms 0.04% 3.980ms 7.959us 500
aten::t 0.04% 3.526ms 0.06% 5.561ms 11.122us 500
aten::view 0.03% 2.611ms 0.03% 2.611ms 8.702us 300
aten::div_ 0.02% 1.973ms 0.04% 4.051ms 40.512us 100
aten::expand 0.02% 1.720ms 0.02% 2.225ms 7.415us 300
AddmmBackward 0.02% 1.601ms 0.37% 34.141ms 341.414us 100
aten::to 0.02% 1.596ms 0.04% 3.871ms 12.902us 300
aten::mean 0.02% 1.485ms 0.10% 9.204ms 92.035us 100
AddBackward0 0.01% 1.381ms 0.01% 1.381ms 1.726us 800
aten::transpose 0.01% 1.297ms 0.02% 2.035ms 4.071us 500
aten::empty_strided 0.01% 1.163ms 0.01% 1.163ms 3.877us 300
MaxPool2DWithIndicesBackward 0.01% 1.095ms 1.03% 94.802ms 948.018us 100
MeanBackward1 0.01% 974.822us 0.16% 14.393ms 143.931us 100
aten::resize_ 0.01% 911.689us 0.01% 911.689us 3.039us 300
aten::zeros_like 0.01% 884.496us 0.11% 10.384ms 103.843us 100
aten::clone 0.01% 798.993us 0.04% 3.687ms 18.435us 200
aten::reshape 0.01% 763.804us 0.03% 2.604ms 13.021us 200
aten::zero_ 0.01% 689.598us 0.13% 11.919ms 59.595us 200
aten::resize_as_ 0.01% 562.349us 0.01% 776.967us 7.770us 100
aten::max_pool2d 0.01% 492.109us 9.49% 874.295ms 8.743ms 100
aten::adaptive_avg_pool2d 0.01% 469.736us 0.10% 9.673ms 96.733us 100
aten::ones_like 0.00% 460.352us 0.01% 1.377ms 13.766us 100
SumBackward0 0.00% 399.188us 0.01% 1.206ms 12.057us 100
aten::flatten 0.00% 397.053us 0.02% 1.917ms 19.165us 100
ViewBackward 0.00% 351.824us 0.02% 1.436ms 14.365us 100
TBackward 0.00% 308.947us 0.01% 1.315ms 13.150us 100
detach 0.00% 127.329us 0.00% 127.329us 2.021us 63
torch::autograd::GraphRoot 0.00% 114.731us 0.00% 114.731us 1.147us 100
aten::detach 0.00% 106.170us 0.00% 233.499us 3.706us 63
--------------------------------------------- ------------ ------------ ------------ ------------ ------------ ------------
Self CPU time total: 9.217sReference
[1] Automatic differentiation package - torch.autograd — PyTorch 1.7.0 documentation
[2] Autograd