summary
HashMap allows null keys and values.
Hashtable does not allow null values or null keys. NullPointerException will be thrown.
The time complexity of get put is constant.
HashMap has two parameters that affect its performance: initial capacity, initial capacity and load factor. Capacity refers to the number of bucket s, that is, the length of the array. The load factor controls how full it can be. The default is 0.75, which better balances the cost of time and space.
When the number of elements exceeds load factor * current capacity, capacity expansion will be triggered. The size of the initial capacity should be specified according to the actual use. If only a few elements are expected, set a smaller initial capacity instead of using the default value of 16; If a large number of elements are expected to be stored, please set a large initial capacity at the beginning rather than allow it to expand multiple times, which will affect the performance of put.
/** * The default initial capacity - MUST be a power of two. * The default initial capacity (number of barrels) must be a power of 2 */ static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16 /** * The maximum capacity, used if a higher value is implicitly specified * by either of the constructors with arguments. * MUST be a power of two <= 1<<30. * Maximum capacity that can be specified by the construction method (number of barrels) < = 1 < < 30 */ static final int MAXIMUM_CAPACITY = 1 << 30; /** * The load factor used when none specified in constructor. * Default load factor */ static final float DEFAULT_LOAD_FACTOR = 0.75f;
HashMap is not synchronized. If multiple threads access an instance at the same time, and at least one thread modifies the Map structurally, it must be synchronized externally. Structural modification is the operation of adding or deleting one or more elements; Modifying the value associated with an existing key is not a structural modification. In other words, adding and deleting are structured modifications, while updating is not. Available Collections can be wrapped into synchronized maps:
Map m = Collections.synchronizedMap(new HashMap(...));
==The collection views of HashMap are all fail fast== For example, the return values of keySet(), entrySet(), and values() methods.
Why not always use the red black tree, but set a threshold 8?
Treenodes are mainly sorted by hashCode. If hashcodes are the same, they will be compared by type. Refer to comparableClassFor(), compareComparables().
Because treenodes are about twice the size of regular nodes, they are used only when there are enough nodes in the container_ THRESHOLD = 8.
When they become too small (due to deletion or resize), they are converted back to normal nodes.
TreeNode is rarely used when hashcodes are evenly distributed.
0: 0.60653066
1: 0.30326533
2: 0.07581633
3: 0.01263606
4: 0.00157952
5: 0.00015795
6: 0.00001316
7: 0.00000094
8: 0.00000006
more: less than 1 in ten million
Implementation of Node
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
}
Why is the hash() method designed like this
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
The reason why the hashCode is shifted to the right by 16 bits and then XOR with itself is to increase the disturbance. int accounts for 4 bytes = 32 bits, index = (tab.length - 1) & hash is used to get the subscript when tab When the length is less than 16 bits, only the low bit of hash will be used in the calculation of subscript. If the high bit is not taken into account, the probability of hash conflict is relatively high. Let the upper 16 bits and the lower 16 bits XOR first, and then the result to the upper tab Length - 1, so that both high and low bits participate in the calculation. If the disturbance is increased, the probability of hash conflict will be smaller.
null hash is equal to 0.
tableSizeFor() returns a power greater than or equal to 2 of cap
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
2N is represented in binary, that is, 1 followed by N zeros. 2N - 1 is n consecutive ones.
// Power 2 = 4 100 11 // Power 4 = 16 10000 1111 ...
Our basic idea is: set all bits after the highest 1 of the digital cap to 1, and then add one to the result to get 2N. However, the premise of this method is that the cap itself cannot be 2N, because this will lead to the wrong result of 2 * cap.
// Positive example: suppose cap is 50 0011 0010 0011 1111 + 0000 0000 = 0100 0000 = 64
// Counterexample: suppose cap is 16 0001 0000 0001 1111 + 0000 0001 0010 0000 = 32
In order to solve the 2N problem of cap itself, we can let int n = cap - 1, perform the above operation with N, and finally add one. In this way, after calculation, the result is still cap.
// Assuming cap is 16, then n = cap - 1 = 15 0001 0000 - 0000 0001 = 0000 1111 // Set the low position to one and actually did nothing 0000 1111 + 0000 0001 = 0001 0000 = 16
How to set the low order to one
n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16;
N | = n > > > 1, n is not equal to zero, so there must be a highest one. We only consider the highest one, and the operation is equivalent to 1x | 01x = 11x. X represents any 0 or 1, which can ensure that the highest one has two adjacent ones:
001xxxxxxxxxxxxx | 001xxxxxxxxxxxx = 0011xxxxxxxxxxxx
N | = n > > > 2, the two highest ones have been obtained in the previous step. This operation can ensure four consecutive ones, 11x | 0011x = 1111x:
0011xxxxxxxxxxxx | 0011xxxxxxxxxx = 001111xxxxxxxxxx
N | = n > > > 4 also repeat the above operation. 1111x | | 0000 1111x = 1111 1111x will get 8 consecutive ones:
001111xxxxxxxxxx | 001111xxxxxx = 0011111111xxxxxx
n |= n >>> 8; n |= n >>> 16; 16 and 32 consecutive ones will be obtained respectively. Since cap is of int type and has 32 bits in total, it needs to be executed to n | = n > > > 16.
Instance variable
// Main memory, which is a power of 2, is initialized when it is used for the first time transient Node<K,V>[] table; // Return value of entrySet() method transient Set<Map.Entry<K,V>> entrySet; // Number of stored elements transient int size; // The number of times the Map is structurally modified to implement the fail fast mechanism transient int modCount; // Threshold of resize = capacity * load factor int threshold; // Load factor final float loadFactor;
Construction method
table [] is delayed initialization. It is not really initialized until put (initialized through the resize() method). Different construction methods will lead to different branches when resizing.
Nonparametric construction method
// loadFactor = 0.75;
// threshold = 0; It will enter the third branch of resize
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
Incoming initial capacity, load factor
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
// If the incoming capacity is too large, the maximum capacity of 1 < < 30 is used
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
// Taking the power greater than or equal to 2 of initialCapacity will enter the second branch of resize
// The return value of tableSizeFor is actually capacity, which is stored in threshold
// You can see from the comment (initial capacity was placed in threshold) in the second branch of resize
this.threshold = tableSizeFor(initialCapacity);
}
Incoming Map
// loadFactor = 0.75;
public HashMap(Map<? extends K, ? extends V> m) {
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);
}
putMapEntries
putMapEntries() will be called by the constructor method and putAll() method.
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
// There are elements in the passed in map
int s = m.size();
if (s > 0) {
// This branch indicates that it is the first put element
// It is possible to call the constructed method
// It can also be instantiated without releasing any elements, and then invoked the putAll() method.
if (table == null) { // pre-size
// According to the reverse calculation capacity of loadFactor, + 1.0F is to round up
float ft = ((float)s / loadFactor) + 1.0F;
// Judge whether the capacity is too large. If it is too large, take the maximum capacity
int t = ((ft < (float)MAXIMUM_CAPACITY) ?
(int)ft : MAXIMUM_CAPACITY);
// Threshold is the old threshold. After recalculating the capacity, the old threshold may not be applicable and needs to be recalculated
if (t > threshold)
threshold = tableSizeFor(t);
}
else if (s > threshold)
resize();
// Put the elements in the specified map into this
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
K key = e.getKey();
V value = e.getValue();
putVal(hash(key), key, value, false, evict);
}
}
}
put,putIfAbsent
Insert or update the key value pair and return the old value associated with the key. null is returned in two cases:
- There was no key
- There was a key, but the old value associated with it was null
Therefore, the return value of the put() method cannot be used to judge whether the key exists. containsKey() must be used.
// Calculate the hash first, and then call putVal()
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
public V putIfAbsent(K key, V value) {
return putVal(hash(key), key, value, true, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node<K,V>[] tab;
Node<K,V> p;
// n is the length of the table array and i is the subscript
int n, i;
// If the table is null or its length is 0, it needs to be expanded (or initialized) before inserting elements
// Only the first insertion will enter this if
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// I = (n - 1) & hash compute subscript
// p is the head of the linked list
// If the position is empty, insert it directly
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// If the location is not empty, you need to traverse the linked list to find the node with key
// If the target node can be found, directly update value to the new value
// If it cannot be found, a new node needs to be added at the end of the linked list
else {
// e represents the target node finally found, which may be empty (there is no target node)
Node<K,V> e;
K k;
// Judge whether the key of p (the head of the linked list) is equal to the key
// The following judgment is equivalent to p.hash = = hash & & objects equals(key, p.key)
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// If equal, assign p to e
e = p;
// Red black tree node
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// In the first if, you have judged the head node of the linked list
// Here, the linked list is traversed from the next Node of the Node to find the Node whose key is equal to the key,
// If the target node can be found, directly update value to the new value
// If it cannot be found, a new node needs to be added at the end of the linked list
// At the same time, binCount is used to record the number of nodes in the linked list in order to upgrade the linked list to a red black tree
for (int binCount = 0; ; ++binCount) {
// Traversed to the end of the linked list, and finally failed to find the target node
if ((e = p.next) == null) {
// Build a new node and append it to the tail of the linked list (tail interpolation method)
p.next = newNode(hash, key, value, null);
// binCount is the number of nodes in the original linked list, excluding the new nodes just inserted,
// binCount + 1 is the number of nodes in the current linked list
// This if judgment is equivalent to if (bincount + 1 > = tree if_threshold)
// After inserting a new node, the length > = 8 will be treelized
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// Judge whether the key of e is equal to the key. If it is equal, the target node is found. Directly jump out of the loop and update value to a new value
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
// If it is not the target node, continue to traverse
// p = e; Equivalent to p = p.next (because e = p.next)
p = e;
}
}
// e == null indicates that the target node is not found. A new node is added at the end of the linked list, and finally null is returned
// e != null indicates that a node with a key equal to key is found, the value needs to be updated, and finally the old value is returned
if (e != null) { // existing mapping for key
V oldValue = e.value;
// onlyIfAbsent is true, which means that put is executed only when the key does not exist, otherwise nothing is done
// In other words, just insert, not update
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
// Number of structural modifications plus one
++modCount;
// Total elements plus one
// If the threshold value is exceeded after insertion, capacity expansion is performed
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
resize
Will be called in two cases:
- Initialization, that is, initializing the main array when adding elements for the first time
- When the space is insufficient and the capacity needs to be expanded
When copy ing the elements of the old array to the new array, there is no violent calculation, but because the size of the array is always 2N, and it is doubled to 2N+1 during capacity expansion. Therefore, the elements in the bucket either stay at the original index position (assuming the index is i), or move 2N right to the bucket with index (i + old capacity). The following examples are given:
Index calculation formula I = (table.length - 1) & hash. After capacity expansion, there is only table The length changed from 2N to 2N+1. We know that 2N is represented in binary as 1 followed by N zeros. 2N - 1 is expressed as binary, which is n consecutive ones. For example, the array length is 32 before capacity expansion and 64 after capacity expansion:
// 32 (5th power of 2), 64 (6th power of 2) It depends on this one ↓ 0010 0000 32 0100 0000 64 0001 1111 31 0011 1111 63 ↑ It depends on this one
Whether the results of 31 & hash and 63 & hash are the same (whether to stay in the original index position) only depends on whether the 6th bit is 0 or 1, and this bit can be judged by hash & 32, that is, if ((e.hash & oldcap) = = 0) in the source code. If it is equal to 0, it will stay in the original index position (i), and if not, it will be placed in the new index position (i + oldCap). For example, 67 and 100:
// 67 original index 3 new index 3 0100 0011 & 0001 1111 31 --------------- 0000 0011 3 0100 0011 & 0011 1111 63 --------------- 0000 0011 3 // 100 original index 4 new index 36 0110 0100 & 0001 1111 31 --------------- 0000 0100 4 0110 0100 & 0011 1111 63 --------------- 0010 0100 36
final Node<K,V>[] resize() {
// Old array
Node<K,V>[] oldTab = table;
// Old capacity - length of old array
int oldCap = (oldTab == null) ? 0 : oldTab.length;
// Old capacity expansion threshold
int oldThr = threshold;
// New capacity and new capacity expansion threshold (0 by default)
int newCap, newThr = 0;
// The old array is not empty, that is, it is not initialized, but the capacity expansion caused by insufficient space
if (oldCap > 0) {
// The old array has exceeded the maximum allowed capacity
if (oldCap >= MAXIMUM_CAPACITY) {
// Set the capacity expansion threshold to the maximum value of Integer and return the old array
// The real capacity expansion is not triggered, and will not be triggered in the future, because it has reached the maximum value
threshold = Integer.MAX_VALUE;
return oldTab;
}
// Newcap = oldcap < < 1. The new capacity is twice the old capacity
// newCap < MAXIMUM_ Capacity, and oldcap > = 16, double the capacity expansion threshold
// When oldcap > = maximum_ When capability or oldcap < 16, it will enter the following if (newThr == 0)
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// The new threshold is twice the old threshold
newThr = oldThr << 1; // double threshold
}
// When the parameter construction method is called and the initial capacity initialCapacity is passed in, it will enter this branch,
// Because the construction method stores the calculated capacity (power of 2) into the threshold, oldcap = = 0 & & oldthr > 0
// Part code this threshold = tableSizeFor(initialCapacity);
else if (oldThr > 0) // initial capacity was placed in threshold
// The initial capacity is put into the threshold variable
// Because oldThr stores the initial capacity, all can be used directly
newCap = oldThr;
// Calling the parameterless construction method will enter this branch
// Because the parameterless construction method does not initialize table [], threshold, so oldcap = = 0 & & oldthreshold = = 0
else { // zero initial threshold signifies using defaults
// An initial threshold of zero indicates that the default value is used
// The new capacity is 16 and the new threshold is 12 = 0.15 * 16
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// Handle oldcap > = maximum in the above oldcap > 0 branch_ Capacity or oldcap < 16
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
// New threshold
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
// New array
table = newTab;
// Move the nodes of the old array to the new array
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
// Only when there are nodes in the bucket, assign the chain header node in the bucket to e
if ((e = oldTab[j]) != null) {
// It is better to set the old GC element to null
oldTab[j] = null;
// There is only one node in the bucket. Directly calculate the subscript and put it into the new array
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// There are multiple nodes in the bucket, and the structure is a red black tree
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
// There are multiple nodes in the bucket, and the structure is a linked list
else { // preserve order
// According to the principle mentioned above, the node can either stay in the original index position J or move to the new index position j + oldCap
// Therefore, the original linked list will be divided into two linked lists, one at index j and the other at index j + oldCap
// Low order linked list, that is, the head and tail of the linked list at position j
Node<K,V> loHead = null, loTail = null;
// The high-order linked list, that is, the head and tail of the linked list at j + oldCap
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// Traverse the linked list. According to the judgment of e.hash & oldcap, if it is equal to 0, it will be added to the linked list lo, otherwise it will be added to the linked list hi
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// Put the lo linked list into the j position of the array
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
// Put the hi linked list into the j + oldCap position of the array
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
get,getOrDefault
Similar to put(), null is returned in two cases:
- There was no key
- There was a key, but the value associated with it was null
Therefore, the return value of the get() method cannot be used to determine whether the key exists. containsKey() must be used.
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
public V getOrDefault(Object key, V defaultValue) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? defaultValue : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// If the array is empty or the node cannot be found according to the subscript, null will be returned directly. Otherwise, traverse the linked list to find the node with the same key
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// The head of the linked list is the target node, which is returned directly
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// If there are multiple nodes in the linked list, traverse the search
if ((e = first.next) != null) {
// Red black tree structure
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// Linked list structure
do {
// If it is the target node, it returns directly
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
// If it is not the target node, continue to traverse
} while ((e = e.next) != null);
}
}
return null;
}
containsKey
containsKey must be used to determine whether the key exists
public boolean containsKey(Object key) {
return getNode(hash(key), key) != null;
}
remove
remove(key) deletes the associated entry of the specified key and returns the value of the deleted entry. As with put(), there are two cases where null is returned.
remove(key, value) deletes the entry with key and value, and returns true when it is successfully deleted.
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
public boolean remove(Object key, Object value) {
return removeNode(hash(key), key, value, true, true) != null;
}
// Does matchValue need to match value
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
// If the array is empty or the node cannot be found according to the subscript, return null directly. Otherwise, traverse the linked list to find the target
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
// Node represents the target node finally found
Node<K,V> node = null, e;
K k; V v;
// First, judge whether the chain header is the target node
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// If yes, assign it to node
node = p;
// There are other nodes in the header chain that are not targets
else if ((e = p.next) != null) {
// Red black tree structure
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
// Linked list structure
else {
// Traverse to find the target node
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
// If found, assign it to node and exit the loop
node = e;
break;
}
// p represents the previous node of e and node
p = e;
// If it cannot be found, continue to traverse
} while ((e = e.next) != null);
}
}
// node != null means that the target node is found (via key) and (does not need to match value or value is matched)
// ! matchValue indicates that no matching value is required
// (v = node. Value) = = value | (value! = null & & value. Equals (V)) indicates that value matches
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// Red black tree delete node
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
// If the chain header is the target node, let the next node of the head node be the chain header
else if (node == p)
tab[index] = node.next;
// If other nodes are target nodes, delete the target node node
else
p.next = node.next;
// Number of structural modifications plus one
++modCount;
// Element data minus one
--size;
afterNodeRemoval(node);
// Returns the deleted target node
return node;
}
}
return null;
}
clear
Simple and crude, empty the array directly
public void clear() {
Node<K,V>[] tab;
modCount++;
if ((tab = table) != null && size > 0) {
size = 0;
for (int i = 0; i < tab.length; ++i)
tab[i] = null;
}
}
containsValue
Whether to include the specified value. Direct double for loop lookup.
A Map may contain a tree node TreeNode. Why can it be traversed as a linked list?
Because treenode extensions LinkedHashMap Entry, and entry extensions HashMap Node, the red black tree node also maintains a two-way linked list.
public boolean containsValue(Object value) {
Node<K,V>[] tab; V v;
if ((tab = table) != null && size > 0) {
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next) {
if ((v = e.value) == value ||
(value != null && value.equals(v)))
return true;
}
}
}
return false;
}
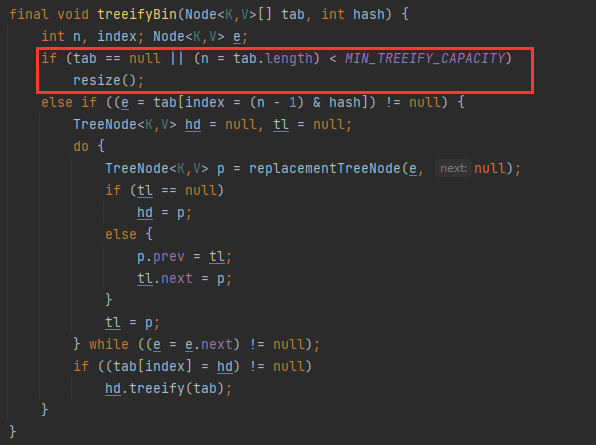
Tree condition
There are two conditions for tree formation:
- Number of elements in bucket > = tree ify_ Threshold (8), as mentioned in the previous put() method
- The length of the array should be > = min_ TREEIFY_ Capability (64), if less than MIN_TREEIFY_CAPACITY will trigger capacity expansion instead of tree