catalogue
1, Definition and introduction of heap
2, How to store binary heap with array?
3, Insert an element into the maximum heap Shift up
4, Remove the element from the maximum heap Shift Down
1, Definition and introduction of heap
Heap is a special data structure in computer science. A heap is usually an array object that can be seen as a tree.
Heap is a binary tree implemented by array. The heap always satisfies the following properties:
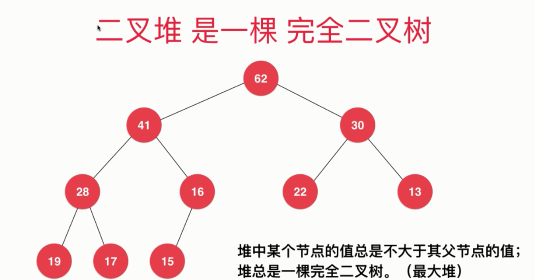
- The value of a node in the heap is always not greater than or less than the value of its parent node.
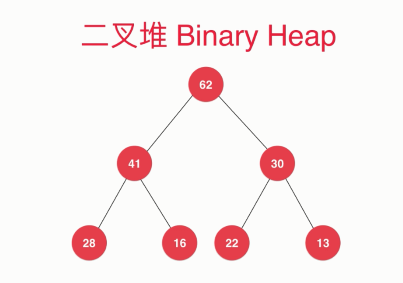
- Heap is always a complete binary tree.
Heap is a nonlinear data structure, equivalent to a one-dimensional array, with two direct successors.
The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap. Common piles include binary pile, Fibonacci pile, etc.
Usage scenario of heap:
- Build priority queue
- Support heap sorting
- Quickly find the minimum (or maximum) value in a set
Next, we mainly analyze a most classic Binary Heap, Binary Heap, and only realize the maximum heap.
Binary heap corresponds to a binary tree. The so-called binary tree is that each node can only have two child nodes at most.
Characteristics of binary tree corresponding to binary heap (maximum heap):
- The value of any node is always no greater than the value of its parent node.
- Must be a complete binary tree.
The so-called complete binary tree is that (1) except for the last layer, the number of nodes in other layers must be the maximum. For a binary tree, the first layer has at most one node, the second layer has at most two nodes, and the third layer has at most four nodes. (2) In the last layer, although the number of nodes may not be the maximum, all nodes must be concentrated on the left.
2, How to store binary heap with array?
Using array to realize binary heap is a very classic implementation‘
We can use arrays to store a binary heap precisely because the heap is a complete binary tree. We can try to label each node of the complete binary tree from top to bottom and from left to right with a serial number, as shown in the figure below. The top node is 1, the lower layer is 2 and 3, the lower layer is 4, 5, 6 and 7, and so on. It is equivalent to marking the sequence number from top to bottom according to the sequence, and then from left to right in each layer.
After labeling the serial number in this way, we can find that for each node, the serial number of the left child node is twice its serial number, and the serial number of the right child node is twice its serial number plus 1.
It should also be noted that here the serial number of the root node is declared as 1. If we declare the serial number of the root node as 0, and so on 0, 1, 2, 3, 4, 5 and 6. At this time, there are similar properties. At this time, the specific calculation rules of the left and right child nodes will change, but there are still corresponding laws. Interested students can try to find this law by themselves.
However, for the heap, a classic implementation is that the root node is marked from 1. In this way, we can store all these data in the array, and the corresponding serial numbers we just marked are the indexes in the array.
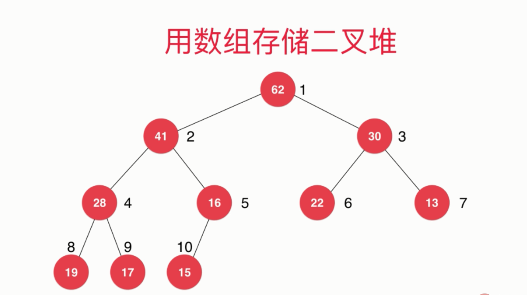
Therefore, the binary heap in the figure above can be stored with the following array.

Note that the 0 index is not used here,
Now that we have such an array, we can easily use the formula we talked about before to find each element in the array, its corresponding left child node element and right child node element. Similarly, we can also find the parent element of each element of the array.
parent(i) = i / 2 / / find the parent node element of i element. Here, the computer division is used. If it cannot be divided, round it down.
left child(i) = 2 * i / / find the left child node element of i element.
right child(i) = 2 * i + 1 / / find the right child node element of i element.
The overall framework of binary heap code implementation is as follows:
public class MaxHeap<T> {
private T[] data;
private int count;
/**
* Constructor to construct an empty heap that can hold capacity elements
* @param capacity
*/
public MaxHeap(int capacity){
data = (T[]) new Object[capacity];
}
/**
* Returns the number of elements in the heap
* @return
*/
public int size(){
return count;
}
/**
* Returns a Boolean value indicating whether the heap is empty
* @return
*/
public boolean isEmpty(){
return count == 0;
}
/**
* Test MaxHeap
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
MaxHeap<Integer> maxHeap = new MaxHeap<Integer>(100);
System.out.println("maxHeap size: " + maxHeap.size());
}
}3, Insert an element into the maximum heap Shift up
Let's take a look at the dynamic demonstration first:
Now there is an existing heap, as shown below.
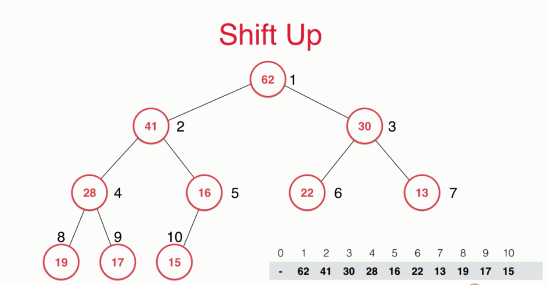
If there is a new element 52, it needs to be added to the maximum heap. From the above analysis, we know that we use a data to implement this heap. Adding a new element to the maximum heap is equivalent to adding an element at the end of the array. At this time, 52 is added to the position with index 11, which means that the maximum heap becomes as follows.
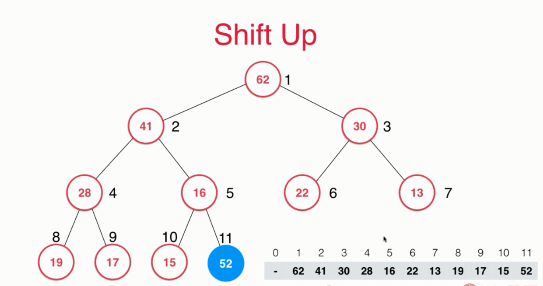
However, you should note that the binary tree like this does not meet the definition of the maximum heap, so next we need to perform some column operations to maintain the definition of the maximum heap. What exactly should we do?
In fact, this process is very simple. Before we add new elements, the whole binary tree is a maximum heap, so the problem must appear on the newly added elements. What we need to do is to adjust the newly added elements to the appropriate position so that the whole binary tree still maintains the nature of maximum heap. So how do we adjust this order?
Compare the newly added element with its parent element. If the parent node element is smaller than the newly added element, which violates the definition of the maximum heap, exchange the positions of the two elements. After the exchange is completed, the binary tree becomes as follows.
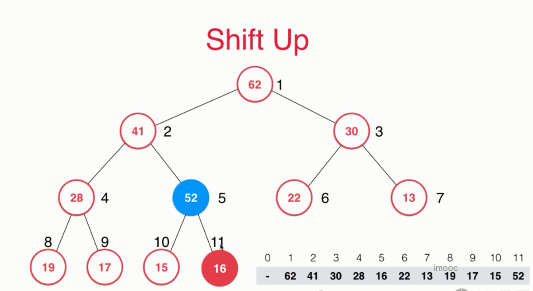
At this time, the new element is the subtree of the root node and has met the definition of maximum heap. In the next step, the new element 52 and its parent node element may not meet the definition of maximum heap. Therefore, at this time, the newly added element 52 is compared with its parent node element 42 to see whether the original parent node is smaller than the new element. Here, the parent node element 41 is smaller than the new element 52, so they have to exchange positions. Now our binary tree looks like this.
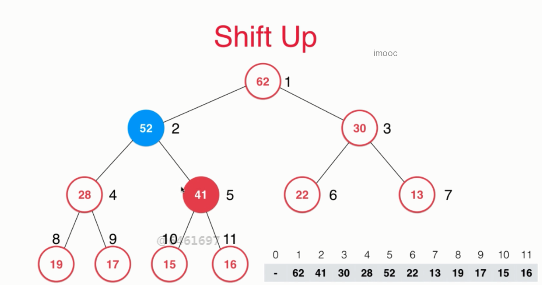
At this time, the new element is the subtree of the root node and still maintains the nature of the maximum heap. Now, in this state, the new element 52 has reached a new position, and it may violate the definition of the maximum heap with its parent node element. Therefore, you need to compare the new element with its parent node element again. 52 is smaller than 62. At this time, you don't need to exchange the positions of the two elements.
After these column operations, we still maintain the definition of the maximum heap of the whole binary tree. We can see that the new element 52 gradually rises from the bottom layer, which is the Shift Up process we want to analyze. In this way, we successfully added new elements to the maximum heap. Let's take a look at the specific code implementation.
/**
* In heap related operations, you need to compare the size of elements in the heap, so E extends Comparable
* @param <E>
*/
public class MaxHeap<E extends Comparable> {
protected E[] data;
protected int count;
protected int capacity;
/**
* Constructor to construct an empty heap that can hold capacity elements
* @param capacity
*/
public MaxHeap(int capacity){
data = (E[]) new Comparable[capacity + 1];
count = 0;
this.capacity = capacity;
}
/**
* Returns the number of elements in the heap
* @return
*/
public int size(){
return count;
}
/**
* Returns a Boolean value indicating whether the heap is empty
* @return
*/
public boolean isEmpty(){
return count == 0;
}
/**
* Inserts a new element into the maximum heap
* @param t
*/
public void insert(E e){
if(count < capacity){
data[count + 1] = e;
count++;
shiftUp(count);
}
}
/**
* The maximum heap core auxiliary function moves the newly inserted element to the appropriate position.
* @param k
*/
private void shiftUp(int k){
while(k > 1 && data[k / 2].compareTo(data[k]) < 0){
swap(k / 2, k);
k = k / 2;
}
}
private void swap(int i, int j){
E temp = data[i];
data[i] = data[j];
data[j] = data[i];
}
}
4, Remove the element from the maximum heap Shift Down
First, let's take a look at the operation flow of Shift Down.
Assume that the following binary tree is the current maximum heap state.
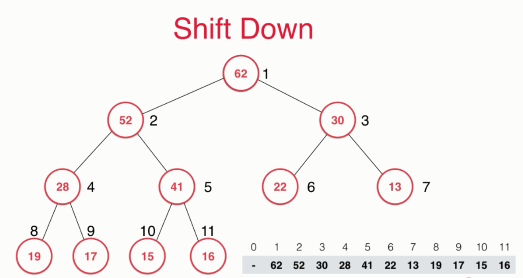
If we want to take an element from the heap, we should pay attention here. Take out an element from the heap, and only the element of the root node can be taken out. For the largest heap, it is equivalent to taking out the element with the highest priority (maximum value).
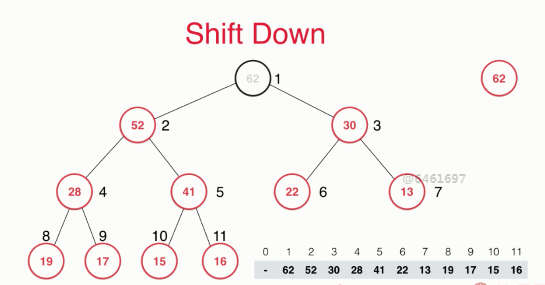
So now we have a missing element in the whole heap. How to fill this element?
The answer is very simple. We just need to put the last element of the whole heap in the position of the first element of the whole heap. At this time, the whole heap is still a complete binary tree,
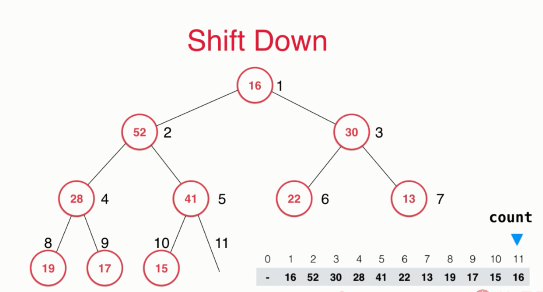
In the previous code implementation, there is a count member variable to describe how many elements are in the current heap. At this time, count --. In this example, the element 16 with index 11 can not be moved. We have set count as the bound in subsequent operations, so the element with index 11 will not be accessed.
In this way, first, we take out an element from the whole heap and still keep it as a complete binary tree. However, we can see that the complete binary tree is not a maximum heap at this time, because we take an element from the bottom and put it on the top. At this time, the root node element is not the maximum value in the whole heap and will be smaller than its child nodes. So the next thing we need to do is to adjust the position of these elements to maintain the nature of the maximum heap.
This adjustment process is actually to move the element of the root node down step by step, and finally find its appropriate position. This is why Shift Down is added to this operation.
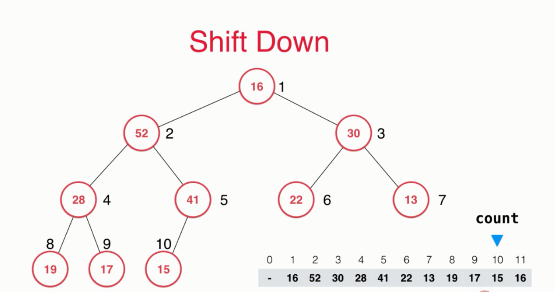
Next, let's take a look at the dynamic demonstration of the whole operation.
Here we move element 16 downward, but it can be left or right, so in which direction?
First compare the sizes of the left child node and the right child node, and then compare the larger child node element with this element. If the larger child node element is larger, exchange the positions of the two elements. Otherwise, do not exchange the positions, and end the whole Shift Down operation. Or when the element is already at the lowest level (without child nodes), you also need to end the whole Shift Down operation.
In this example, the left node element 52 is larger than the right node element 30, and the left node element 52 is larger than the element 16, so the element 16 is replaced with the left node element 52. Because after such replacement, it can be ensured that element 52 is larger than element 16 and element 32.
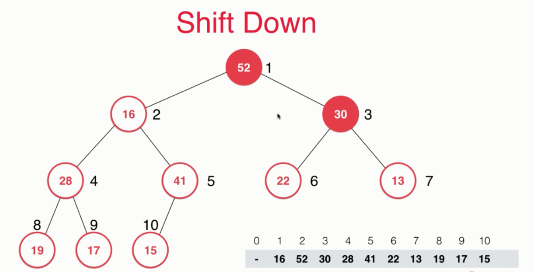
Next, we continue to move down and compare the left and right child node elements 28 and 41 of element 16. The right node element 41 is larger than the left node element 28, and the right node element 41 is larger than the element 16. Therefore, element 16 and right child node element 41 exchange positions.
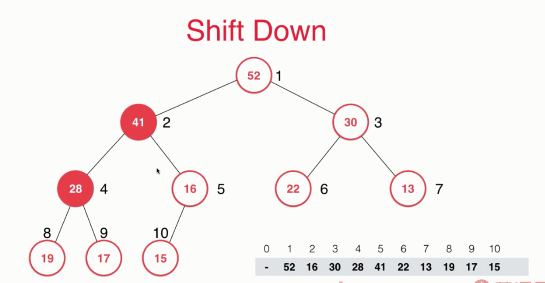
At this time, element 16 continues to compare with its child node elements. At this time, element 16 has only left child nodes, so only element 16 and left child node element 15 need to be compared. Element 16 is larger than left child node element 15, so no exchange is required. So far, our Shift Down operation is over.
At this time, our maximum heap successfully exits an element 62, and then continues to maintain the nature of the maximum heap through the Shift Down operation. Next, if we want to push out the element, the root element 52 will be pushed out. Then element 15 will be replaced, and then through some column Shift Down operations to maintain the nature of the maximum heap.
Let's take a look at the specific code implementation.
/**
* In heap related operations, you need to compare the size of elements in the heap, so E extends Comparable
* @param <E>
*/
public class MaxHeap<E extends Comparable> {
protected E[] data;
protected int count;
protected int capacity;
/**
* Constructor to construct an empty heap that can hold capacity elements
* @param capacity
*/
public MaxHeap(int capacity){
data = (E[]) new Comparable[capacity + 1];
count = 0;
this.capacity = capacity;
}
/**
* Returns the number of elements in the heap
* @return
*/
public int size(){
return count;
}
/**
* Returns a Boolean value indicating whether the heap is empty
* @return
*/
public boolean isEmpty(){
return count == 0;
}
/**
* Inserts a new element into the maximum heap
* @param t
*/
public void insert(E e){
if(count < capacity){
data[count + 1] = e;
count++;
shiftUp(count);
}
}
/**
* The maximum heap core auxiliary function moves the newly inserted element to the appropriate position.
* @param k
*/
private void shiftUp(int k){
while(k > 1 && data[k / 2].compareTo(data[k]) < 0){
swap(k / 2, k);
k = k / 2;
}
}
/**
* Take out the largest element in the largest heap
* @return
*/
public E extractMax(){
if(count <= 0){
return null;
}
E e = data[1];
swap(1, count);
count --;
shiftDown(1);
return e;
}
/**
* The maximum heap core auxiliary function moves the elements of the root node to the appropriate position.
* @param k
*/
private void shiftDown(int k){
while(k * 2 <= count){ //Judge whether node k has child nodes. As long as there is a right node, there must be child nodes
int j = k * 2; //In this cycle, data[k] and data[j] exchange positions
if(j + 1 <= count && data[j + 1].compareTo(data[j]) > 0){
//There are right child nodes, and the right child node element is larger than the left child node element.
j ++;
}
// data[j] is the maximum of data[2*k] and data[2*k+1]
if(data[k].compareTo(data[j]) >= 0){
//Node k is already larger than all its child nodes and does not need to exchange locations.
break;
}
swap(k, j);
k = j;
}
}
private void swap(int i, int j){
E temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
5, Summary
Heap is a flexible and dynamic data structure, which can keep the maximum (or small) element of the root node after constantly adding and removing elements. Due to this feature, heap is very suitable for implementing priority queues and sorting (heap sorting).