Contravariant and covariant are C#4 new concepts. Many books and blogs have explained them. I don't think they have been explained clearly. After understanding them, we can define generic delegates and interfaces more accurately. Here I try to draw a diagram to analyze contravariant and covariant in detail.

Concept of change

We all know Net or in the world of OO, you can safely assign the reference of the subclass to the reference of the parent class, for example:

//Parent = child
string str = "string";
object obj = str;//Changed

C # also has the concept of genericity. Genericity is a further abstraction of the type system, which is higher than the above simple types. Reflecting the above changes in the parameters of generics is what we call the concept of inversion and covariance. By using in or out keywords on generic parameters, you can get the ability of inversion or covariance. Here are some examples of comparison:

Covariance (foo < parent > = foo < child >):

//Generic delegate:
public delegate T MyFuncA<T>();//Inversion and covariance are not supported
public delegate T MyFuncB<out T>();//Support covariance
 
MyFuncA<object> funcAObject = null;
MyFuncA<string> funcAString = null;
MyFuncB<object> funcBObject = null;
MyFuncB<string> funcBString = null;
MyFuncB<int> funcBInt = null;
 
funcAObject = funcAString;//Compilation failed. MyFuncA does not support inversion and covariance
funcBObject = funcBString;//Changed, covariant
funcBObject = funcBInt;//Compilation failed, value type does not participate in covariance or inversion
 
//generic interface 
public interface IFlyA<T> { }//Inversion and covariance are not supported
public interface IFlyB<out T> { }//Support covariance
 
IFlyA<object> flyAObject = null;
IFlyA<string> flyAString = null;
IFlyB<object> flyBObject = null;
IFlyB<string> flyBString = null;
IFlyB<int> flyBInt = null;
 
flyAObject = flyAString;//Compilation failed. IFlyA does not support inversion and covariance
flyBObject = flyBString;//Changed, covariant
flyBObject = flyBInt;//Compilation failed, value type does not participate in covariance or inversion
 
//Array:
string[] strings = new string[] { "string" };
object[] objects = strings;

Inverse (foo < subclass > = foo < parent >)

public delegate void MyActionA<T>(T param);//Inversion and covariance are not supported
public delegate void MyActionB<in T>(T param);//Support inverter
 
public interface IPlayA<T> { }//Inversion and covariance are not supported
public interface IPlayB<in T> { }//Support inverter
 
MyActionA<object> actionAObject = null;
MyActionA<string> actionAString = null;
MyActionB<object> actionBObject = null;
MyActionB<string> actionBString = null;
actionAString = actionAObject;//MyActionA does not support inversion and covariance. Compilation failed
actionBString = actionBObject;//Changed, reversed
 
IPlayA<object> playAObject = null;
IPlayA<string> playAString = null;
IPlayB<object> playBObject = null;
IPlayB<string> playBString = null;
playAString = playAObject;//IPlayA does not support inversion and covariance. Compilation failed
playBString = playBObject;//Changed, reversed

 

Here we see that some can change and some cannot. We should know the following points:

• Previous generic systems (or when there is no in/out keyword) cannot be "changed", whether it is "inverse" or "CIS".
• Currently, only the inversion and covariance of interfaces and delegates are supported, and classes and methods are not supported. But arrays also have covariance.
• Value types do not participate in inversion and covariance.

So what does in/out mean? Why do we have the ability to "change" by adding them? Should we add them when defining generic delegates or interfaces?

Originally, if the in keyword is added to the generic parameter as the generic modifier, the generic parameter can only be used as the input parameter of the method, or only write the parameter of the attribute, not as the return value of the method. In short, it can only be "in" and not out. The out keyword is the opposite.

When trying to compile the following generic interface that uses the in generic parameter as the return value of the method:

public interface IPlayB<in T>
{
    T Test();
}

The following compilation errors occurred:

Error {1} invalid variance: type parameter't 'must be a valid covariant on' covarianceandcontravariance. Iplayb < T >. Test() '. "T" is inverse.   

So far, we have roughly known the related concepts of inversion and covariance, so why can we "change" by limiting the generic parameter to in or out? Now try to draw pictures to explain the principle.

Covariance is not taken for granted, and inversion has no "inverse"

Let's first look at generic types that do not support inversion and covariance, assign subclasses to the parent class, and then execute the specific process of the parent class method. For such a simple example, the Test method:

public interface Base<T>
{
    T Test(T param);
}
public class Sub<T> : Base<T>
{
    public T Test(T param) { return default(T); }
}
Base<string> b = new Sub<string>();
b.Test("");

Its actual process is as follows:

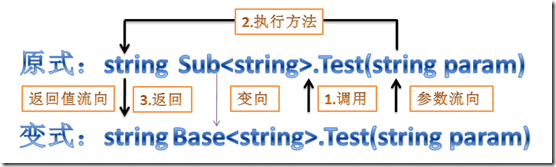
That is, calling the method of the parent class is actually calling the method of the child class. It can be seen that this method can be called safely, which requires two conditions: 1 The method parameters of the variant (parent) can be safely converted to the parameters of the original formula (child); 2. The return value of the original formula (sub) can be safely converted to the return value of the variant. Unfortunately, the flow direction of the parameter is opposite to the flow direction of the return value, so it must not work for generic parameters that are both in and out, and one direction must not be safely converted. For example, for the above example, we try to "change":

Base<object> BaseObject = null;
Base<string> BaseString = null;
BaseObject = BaseString;//Compilation failed
BaseObject.Test("");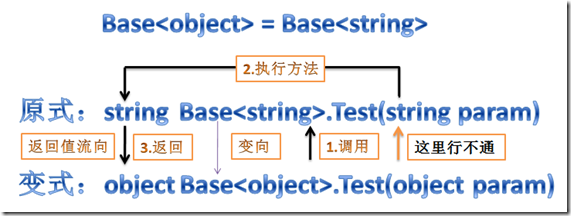

If we can understand here, it is not difficult for us to get the "actual flow chart" of inversion and covariance (remember, they have in/out restrictions):

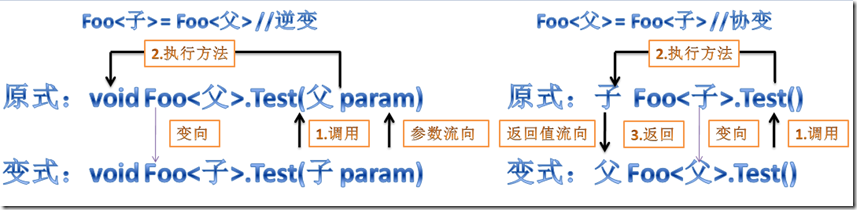
It can be seen that from the "actual flow chart", there is no "inversion" at all, which is inseparable from the fact that we can only safely assign the reference of the subclass to the reference of the parent class.

You should basically understand inversion and covariance here, but it's important to assemble your head This article There is a more advanced question, which is also answered in the original text. Here I understand it in the way of drawing above.

Illustration of the interaction between inversion and covariance

Do you know that the question is correct?

public interface IBar<in T> { }
//It should be in
public interface IFoo<in T>
{
    void Test(IBar<T> bar);
}
//Or out
public interface IFoo<out T>
{
    void Test(IBar<T> bar);
}

The answer is that if it is in, the compilation will fail and out will be correct (of course, it can be compiled without generic modifiers, but IFoo has no covariance ability). This means that when a generic type (IBar) with covariant (inverse) ability is used as a parameter of another generic type (IFoo), it affects the definition of its generic type (IFoo). At first glance, one of the traps thought to be in is that t is in the parameters of the Test method, so it is thought to be in. But the parameter of Test here is not t at all, but IBar < T >.

Let's draw a picture to understand it. Since out can pass, its "covariant flow chart" should be as follows:

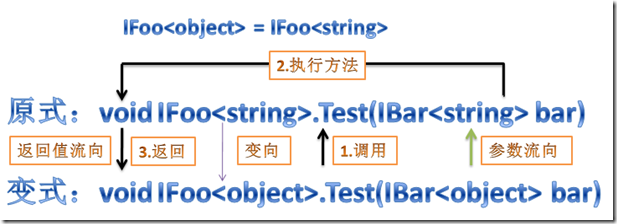
The figure is roughly the same as the previous ones, but understanding it should be opposite to the problem (the above problem is to define IBar first, and then IFoo). 1. We define an IFoo with covariant ability, which is the premise. 2. Yes, the above process is established. 3. The key point of this process is the parameter flow direction. In order to establish the whole process, IBar < string > = IBar < Object > must be established. Isn't this the inversion? The whole conclusion is that IFoo with covariant ability requires its generic parameter (IBar) to have inversion ability. In fact, it can also be understood from the arrow above, because the direction of the original formula and variant is opposite to that of the parameter, which leads to their opposite ability. This is what the assembly head article says: the covariant inverse exchange principle of method parameters. According to this principle, it is also easy to conclude that if the return value of the Test method is IBar < T > rather than a parameter, IBar < T > is required to have covariant ability, because the arrow of the return value is in the same direction as the arrow of the original formula and variant.