1, Demand

Please enter an expression calculation formula: [722-5 + 1-5 + 3-3] Click calculation [as shown below]

Excuse me: how does the bottom layer of the computer calculate the result? Note that it is not a simple operation to list the formula, because we look at the formula 7 * 2 * 2 - 5, but how the computer understands the formula (for the computer, what it receives is a string), we are discussing this problem. - > Stack

2, Introduction to stack

1. Stack (stack)
2. A stack is an ordered list of Filo first in last out.
3. Stack is a special linear table that restricts the insertion and deletion of elements in a linear table to the same end of the linear table. The end that allows insertion and deletion is the changing end, which is called the top of the stack, and the other end is the fixed end, which is called the bottom of the stack.
4. According to the definition of stack, the first element put into the stack is at the bottom of the stack, the last element put into the stack is at the top of the stack, while the deleted element is just the opposite. The last element put into the stack is deleted first, and the first element is deleted last

Graphically illustrate the concepts of pop and push:

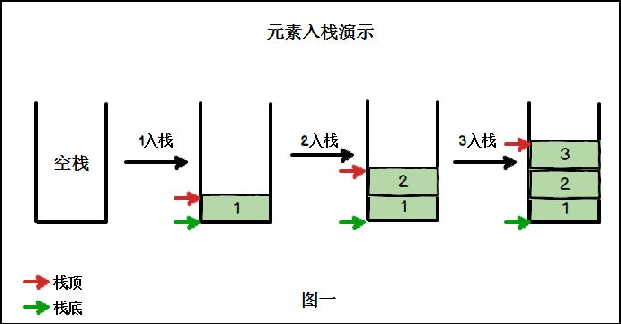
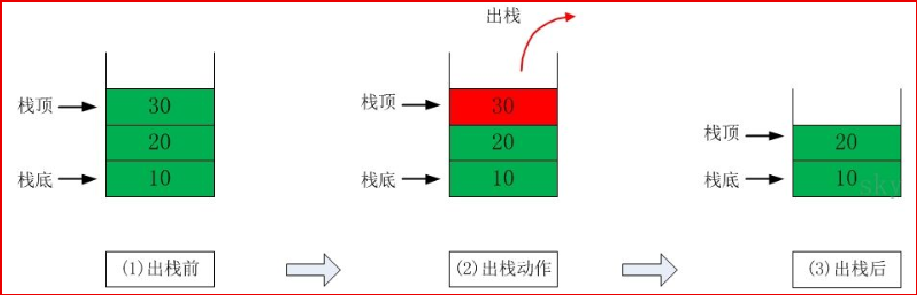
3, Application scenario of stack

1. Subroutine call: before jumping to the subroutine, the address of the next instruction will be stored in the stack until the subroutine is executed, and then the address will be taken out to return to the original program.
2. Handling recursive calls: similar to subroutine calls, except that in addition to storing the address of the next instruction, parameters, area variables and other data are also stored in the stack.
3. Expression conversion [infix expression to suffix expression] and evaluation (practical solution).
4. Traversal of binary tree.
5. depth first search method of graphics.

4, Quick start to stack

4.1 array simulation stack

Use the array to simulate the use of the stack. Since the stack is an ordered list, of course, the structure of the array can be used to store the data content of the stack. Next, we will use the array to simulate the operations such as out of the stack and in the stack.

Realize the analysis of ideas and draw a schematic diagram

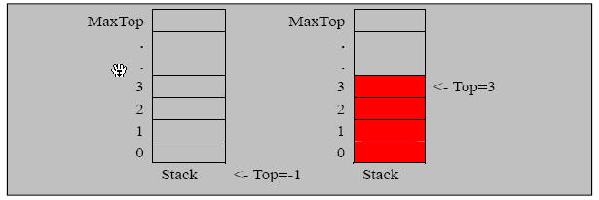
Thought analysis of realizing stack

1. Use arrays to simulate stacks
2. Define a top to represent the top of the stack and initialize it to - 1
3. When data is added to the stack, top++; stack[top] = data;
4. Stack out operation, int value = stack[top]; top–, return value

Code implementation:

//Define an ArrayStack to represent the stack
class ArrayStack {
	private int maxSize; // Stack size
	private int[] stack; // Array, array simulation stack, data is placed in the array
	private int top = -1;// Top represents the top of the stack and is initialized to - 1
	
	//constructor 
	public ArrayStack(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[this.maxSize];
	}
	
	//Stack full
	public boolean isFull() {
		return top == maxSize - 1;
	}
	//Stack empty
	public boolean isEmpty() {
		return top == -1;
	}
	//Stack push
	public void push(int value) {
		//First judge whether the stack is full
		if(isFull()) {
			System.out.println("Stack full");
			return;
		}
		top++;
		stack[top] = value;
	}
	//Out of stack - pop to return the data at the top of the stack
	public int pop() {
		//First judge whether the stack is empty
		if(isEmpty()) {
			//Throw exception
			throw new RuntimeException("Stack empty, no data~");
		}
		int value = stack[top];
		top--;
		return value;
	}
	//Display the stack [traversing the stack]. When traversing, you need to display data from the top of the stack
	public void list() {
		if(isEmpty()) {
			System.out.println("Stack empty, no data~~");
			return;
		}
		//Start from the top of the stack
		for(int i = top; i >= 0 ; i--) {
			System.out.printf("stack[%d]=%d\n", i, stack[i]);
		}
	}
	
}

4.2 linked list to simulate stack

public class LinkStackDemo {
    private int size;// Stack size
    private HeroNode head = new HeroNode(-1,"","");// Top represents the top of the stack and is initialized to - 1

    //Stack empty
    public boolean isEmpty() {
        return head.next == null;
    }
    //Stack push
    public void push(HeroNode node) {
        size++;
        node.next = head.next;
        head.next = node;
    }
    //Out of stack - pop to return the data at the top of the stack
    public HeroNode pop() {
        //First judge whether the stack is empty
        if(isEmpty()) {
            //Throw exception
            throw new RuntimeException("Stack empty, no data~");
        }
        HeroNode node = head.next;
        head.next = head.next.next;
        return node;
    }
    //Display the stack [traversing the stack]. When traversing, you need to display data from the top of the stack
    public void list() {
        if(isEmpty()) {
            System.out.println("Stack empty, no data~~");
            return;
        }
        //You need to display data from the top of the stack
        HeroNode temp = head;
        while (temp.next != null){
            System.out.println(temp.next);
            temp.next=temp.next.next;
        }
    }
}

class HeroNode {
    public int no;
    public String name;
    public String nickname;
    public HeroNode next; //Point to next node
    //constructor 
    public HeroNode(int no, String name, String nickname) {
        this.no = no;
        this.name = name;
        this.nickname = nickname;
    }
    //To display the method, we re toString
    @Override
    public String toString() {
        return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
    }
}

5, Stack implementation synthesis calculator (infix expression)

Use the stack to complete the calculation of the result of an expression
722-5+1-5+3-4 = ？

Train of thought analysis (diagram):

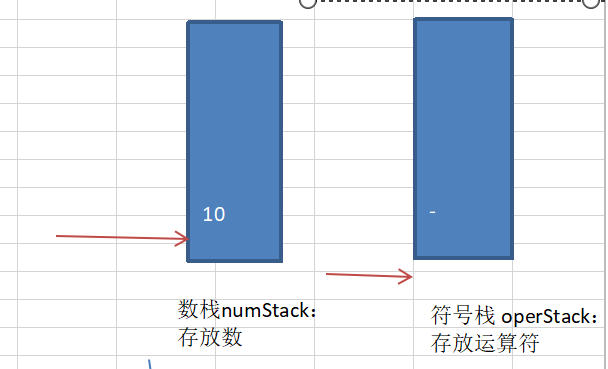
Calculation idea of using stack to complete expression

1. Traverse our expression through an index value (index)
2. If we find that it is a number, we will directly enter the number stack
3. If it is found that a symbol is scanned, it can be divided into the following situations
   3.1 if the current symbol stack is found to be empty, it will be directly put into the stack
   3.2 if there are operators in the symbol stack, compare them. If the priority of the current operator is less than or equal to that of the operator in the stack, you need to pop two numbers from the number stack, pop a symbol from the symbol stack, operate, get the result, put it into the number stack, and then put the current operator into the symbol stack,
   If the priority of the current operator is higher than that of the operator in the stack, it is directly put into the symbol stack
4. When the expression is scanned, pop out the corresponding numbers and symbols from the number stack and symbol stack in sequence and run
5. Finally, there is only one number in the number stack, which is the result of the expression

Cost realization:

package com.atguigu.stack;

public class Calculator {

	public static void main(String[] args) {
		//Complete the operation of the expression according to the previous teacher's ideas
		String expression = "7*2*2-5+1-5+3-4"; // 15 / / how to deal with the problem of multiple bits?
		//Create two stacks, number stack and one symbol stack
		ArrayStack2 numStack = new ArrayStack2(10);
		ArrayStack2 operStack = new ArrayStack2(10);
		//Define the relevant variables required
		int index = 0;//For scanning
		int num1 = 0; 
		int num2 = 0;
		int oper = 0;
		int res = 0;
		char ch = ' '; //Save the char obtained from each scan to ch
		String keepNum = ""; //Multi bit number for splicing
		//Start scan expression of while loop
		while(true) {
			//Get each character of expression in turn
			ch = expression.substring(index, index+1).charAt(0);
			//Judge what ch is and deal with it accordingly
			if(operStack.isOper(ch)) {//If operator
				//Judge whether the current symbol stack is empty
				if(!operStack.isEmpty()) {
					//If there are operators in the symbol stack, compare them. If the priority of the current operator is less than or equal to the operator in the stack, you need to pop out two numbers from the number stack,
					//pop out a symbol from the symbol stack, perform the operation, get the result, put it into the number stack, and then put the current operator into the symbol stack
					if(operStack.priority(ch) <= operStack.priority(operStack.peek())) {
						num1 = numStack.pop();
						num2 = numStack.pop();
						oper = operStack.pop();
						res = numStack.cal(num1, num2, oper);
						//Stack the result of the operation as a number
						numStack.push(res);
						//Then put the current operator on the symbol stack
						operStack.push(ch);
					} else {
						//If the priority of the current operator is higher than that of the operator in the stack, it is directly put into the symbol stack
						operStack.push(ch);
					}
				}else {
					//If it is empty, direct access symbol stack
					operStack.push(ch); // 1 + 3
				}
			} else { //If it is a number, it is directly put into the number stack
				
				//numStack.push(ch - 48); //? "1+3" '1' => 1
				//Analysis ideas
				//1. When processing multi digit numbers, if it cannot be found that it is a number, it will be immediately put into the stack, because it may be multi digit numbers
				//2. When processing numbers, you need to look at one bit after the index of the expression. If it is a number, it will be scanned. If it is a symbol, it will be put on the stack
				//3. Therefore, we need to define a variable string for splicing
				
				//Number of processing bits
				keepNum += ch;
				
				//If ch is already the last bit of expression, it is directly put on the stack
				if (index == expression.length() - 1) {
					numStack.push(Integer.parseInt(keepNum));
				}else{
				
					//Judge whether the next character is a number. If it is a number, continue scanning. If it is an operator, put it on the stack
					//Note that it's the last one, not the index++
					if (operStack.isOper(expression.substring(index+1,index+2).charAt(0))) {
						//If the last bit is an operator, put keepNum = "1" or "123" on the stack
						numStack.push(Integer.parseInt(keepNum));
						//important!!!!!!, keepNum empty
						keepNum = "";
						
					}
				}
			}
			//Let index + 1 and judge whether to scan to the end of expression
			index++;
			if (index >= expression.length()) {
				break;
			}
		}
		
		//When the expression is scanned, pop out the corresponding numbers and symbols from the number stack and symbol stack in sequence and run
		while(true) {
			//If the symbol stack is empty, the final result will be calculated, and there is only one number [result] in the number stack
			if(operStack.isEmpty()) {
				break;
			}
			num1 = numStack.pop();
			num2 = numStack.pop();
			oper = operStack.pop();
			res = numStack.cal(num1, num2, oper);
			numStack.push(res);//Push 
		}
		//pop out the last number of the stack, which is the result
		int res2 = numStack.pop();
		System.out.printf("expression %s = %d", expression, res2);
	}

}

//First create a stack and use it directly
//Define an ArrayStack2 representation stack, which needs to be extended
class ArrayStack2 {
	private int maxSize; // Stack size
	private int[] stack; // Array, array simulation stack, data is placed in the array
	private int top = -1;// Top represents the top of the stack and is initialized to - 1
	
	//constructor 
	public ArrayStack2(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[this.maxSize];
	}
	
	//Add a method to return the value at the top of the current stack, but it is not a real pop
	public int peek() {
		return stack[top];
	}
	
	//Stack full
	public boolean isFull() {
		return top == maxSize - 1;
	}
	//Stack empty
	public boolean isEmpty() {
		return top == -1;
	}
	//Stack push
	public void push(int value) {
		//First judge whether the stack is full
		if(isFull()) {
			System.out.println("Stack full");
			return;
		}
		top++;
		stack[top] = value;
	}
	//Out of stack - pop to return the data at the top of the stack
	public int pop() {
		//First judge whether the stack is empty
		if(isEmpty()) {
			//Throw exception
			throw new RuntimeException("Stack empty, no data~");
		}
		int value = stack[top];
		top--;
		return value;
	}
	//Display the stack [traversing the stack]. When traversing, you need to display data from the top of the stack
	public void list() {
		if(isEmpty()) {
			System.out.println("Stack empty, no data~~");
			return;
		}
		//You need to display data from the top of the stack
		for(int i = top; i >= 0 ; i--) {
			System.out.printf("stack[%d]=%d\n", i, stack[i]);
		}
	}
	//Returns the priority of the operator. The priority is determined by the programmer. The priority is expressed in numbers
	//The higher the number, the higher the priority
	public int priority(int oper) {
		if(oper == '*' || oper == '/'){
			return 1;
		} else if (oper == '+' || oper == '-') {
			return 0;
		} else {
			return -1; // Assume that the current expression is only +, -, */
		}
	}
	//Judge whether it is an operator
	public boolean isOper(char val) {
		return val == '+' || val == '-' || val == '*' || val == '/';
	}
	//computing method
	public int cal(int num1, int num2, int oper) {
		int res = 0; // res is used to store the calculation results
		switch (oper) {
		case '+':
			res = num1 + num2;
			break;
		case '-':
			res = num2 - num1;// Pay attention to the order
			break;
		case '*':
			res = num1 * num2;
			break;
		case '/':
			res = num2 / num1;
			break;
		default:
			break;
		}
		return res;
	}
	
}

6, Inverse calculator (Poland)

We have completed an inverse Polish calculator and are required to complete the following tasks:

1. Enter an inverse Polish expression (suffix expression), use stack, and calculate the result
2. It supports parentheses and multi digit integers, because here we mainly talk about data structures, so the calculator is simplified and only supports the calculation of integers.
3. Train of thought analysis

For example: (3 + 4) × The suffix expression corresponding to 5-6 is 3, 4 + 5 × 6 -, evaluate the suffix expression as follows:
1. Scan from left to right and press 3 and 4 into the stack;
2. Encounter the + operator, so pop up 4 and 3 (4 is the top element of the stack and 3 is the secondary top element), calculate the value of 3 + 4, get 7, and then put 7 on the stack;
3. Put 5 into the stack;
4. Next is × Operator, so pop up 5 and 7 and calculate 7 × 5 = 35, put 35 into the stack;
5. Stack 6;
6. Finally, the - Operator calculates the value of 35-6, i.e. 29, so as to obtain the final result

Code completion:

public class PolandNotation2 {

	public static void main(String[] args) {

		//First define the inverse Polish expression
		// (30+4)×5-6 => 30 4 + 5 × 6 - => 164
		// 4 * 5 - 8 + 60 + 8 / 2 => 4 5 * 8 - 60 + 8 2 / +
		// test 
		// Note for convenience, the numbers and symbols of the inverse Polish expression are separated by spaces 
		 String suffixExpression = "30 4 + 5 * 6 -"; 
		// thinking 
		// 1. First "30 4 + 5" ×  6 - "= > put in ArrayList 
		// 2. Pass the ArrayList to a method, traverse the ArrayList and complete the calculation with the stack 
		List<String> list = getListString(suffixExpression); 
		System.out.println("rpnList=" + list);
		int res = calculate(list); System.out.println("The result of the calculation is=" + res);
	}
	
	//Put an inverse Polish expression, and put the data and operators into the ArrayList in turn
	public static List<String> getListString(String suffixExpression) {
		//Split suffixExpression
		String[] split = suffixExpression.split(" ");
		List<String> list = new ArrayList<String>();
		for(String ele: split) {
			list.add(ele);
		}
		return list;
		
	}
	
	//Complete the operation of the inverse Polish expression
	/*
	 * 1)Scan from left to right and press 3 and 4 into the stack;
		2)Encounter the + operator, so pop up 4 and 3 (4 is the top element of the stack and 3 is the secondary top element), calculate the value of 3 + 4, get 7, and then put 7 on the stack;
		3)Put 5 into the stack;
		4)Next is × Operator, so pop up 5 and 7 and calculate 7 × 5 = 35, put 35 into the stack;
		5)Put 6 into the stack;
		6)Finally, the - Operator calculates the value of 35-6, i.e. 29, so as to obtain the final result
	 */
	
	public static int calculate(List<String> ls) {
		// To create a stack, you only need one stack
		Stack<String> stack = new Stack<String>();
		// Traversal ls
		for (String item : ls) {
			// Regular expressions are used here to extract numbers
			if (item.matches("\\d+")) { // The number of multiple bits matches
				// Push 
				stack.push(item);
			} else {
				// pop out two numbers, operate them, and then put them on the stack
				int num2 = Integer.parseInt(stack.pop());
				int num1 = Integer.parseInt(stack.pop());
				int res = 0;
				if (item.equals("+")) {
					res = num1 + num2;
				} else if (item.equals("-")) {
					res = num1 - num2;
				} else if (item.equals("*")) {
					res = num1 * num2;
				} else if (item.equals("/")) {
					res = num1 / num2;
				} else {
					throw new RuntimeException("Incorrect operator");
				}
				//Put res on the stack
				stack.push("" + res);
			}
			
		}
		//The last data left in the stack is the result of the operation
		return Integer.parseInt(stack.pop());
	}

}

7, Convert infix expression to suffix expression

As you can see, the suffix expression is suitable for calculation, but it is not easy for people to write it, especially when the expression is very long. Therefore, in the development, we need to convert the infix expression into the suffix expression.

Example: find infix expression 1 + ((2 + 3) × 4) - suffix expression of 5.

Ideas and diagrams:

1. Initialize two stacks: operator stack s1 and stack s2 for storing intermediate results;
2. Scan infix expression from left to right;
3. When encountering an operand, press it to s2;
4. When an operator is encountered, compare its priority with s1 stack top operator:
   1. If s1 is empty or the operator at the top of the stack is an open parenthesis "(", this operator will be directly put on the stack;
   2. Otherwise, if the priority is higher than the operator at the top of the stack, press the operator into s1;
   3. Otherwise, pop up the operator at the top of s1 stack and press it into s2, go to (4.1) again and compare it with the new operator at the top of s1 stack;
5. When parentheses are encountered:
   (1) If it is an open bracket "(", press s1 directly
   (2) If it is the closing parenthesis ")", the operators at the top of s1 stack will pop up in turn and press s2 until the left parenthesis is encountered. At this time, this pair of parentheses will be discarded
6. Repeat steps 2 through 5 until the rightmost part of the expression
7. Pop up the remaining operators in s1 and press them into s2
8. Pop up the elements in s2 in turn and output them. The reverse order of the result is the suffix expression corresponding to the infix expression

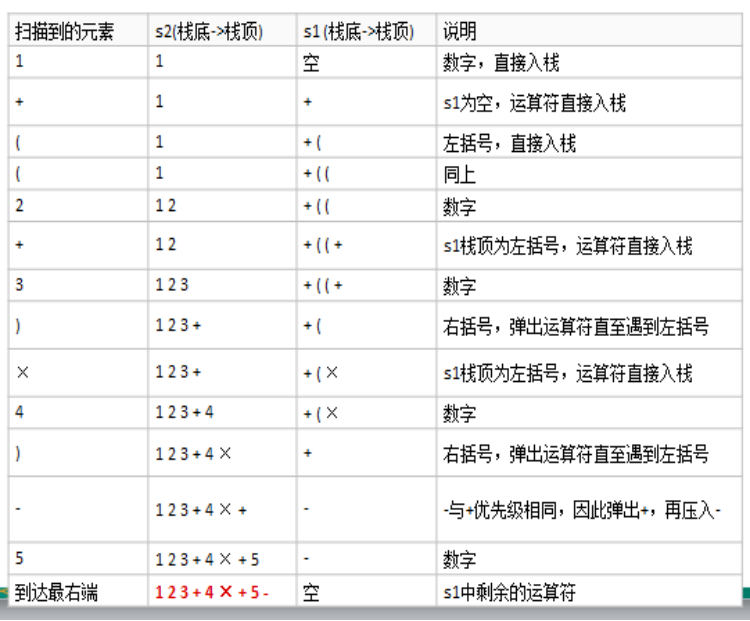
Note: some students may go deep into how this idea is deduced. In fact, it is deduced reversely from the previous example, so it is more troublesome to express. Just remember this idea.

8, Inverse Polish calculator (full version)

public class PolandNotation {

	public static void main(String[] args) {
		
		
		//Complete the function of converting an infix expression into a suffix expression
		//explain
		//1. 1+((2+3) × 4) - 5 = > turn to 1 2 3 + 4 × +  5 –
		//2. Because it is inconvenient to operate str directly, first put "1 + ((2 + 3) × 4) - 5 "=" List corresponding to the expression of infix
		//   I.e. "1 + ((2 + 3)) × 4)-5" => ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
		//3. List corresponding to infix expression = > list corresponding to suffix expression
		//   That is, ArrayList [1,+,(,(,2,+,3,),*,4,),-,5] = "ArrayList [1,2,3,+,4,*,+,5, –]
		
		String expression = "1+((2+3)*4)-5";//Note the expression 
		List<String> infixExpressionList = toInfixExpressionList(expression);
		System.out.println("Infix expression List=" + infixExpressionList); // ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
		List<String> suffixExpreesionList = parseSuffixExpreesionList(infixExpressionList);
		System.out.println("Corresponding to suffix expression List" + suffixExpreesionList); //ArrayList [1,2,3,+,4,*,+,5,–] 
		
		System.out.printf("expression=%d", calculate(suffixExpreesionList)); // ?
		
		
		
		/*
		
		//First define the inverse Polish expression
		//(30+4)×5-6  => 30 4 + 5 × 6 - => 164
		// 4 * 5 - 8 + 60 + 8 / 2 => 4 5 * 8 - 60 + 8 2 / + 
		//test 
		//Note for convenience, the numbers and symbols of the inverse Polish expression are separated by spaces
		//String suffixExpression = "30 4 + 5 * 6 -";
		String suffixExpression = "4 5 * 8 - 60 + 8 2 / +"; // 76
		//thinking
		//1. First put "3, 4 + 5" ×  6 - "= > put in ArrayList
		//2. Pass the ArrayList to a method to traverse the ArrayList and complete the calculation with the stack
		
		List<String> list = getListString(suffixExpression);
		System.out.println("rpnList=" + list);
		int res = calculate(list);
		System.out.println("The result of calculation is = "+ res);
		
		*/
	}
	
	
	
	//That is, ArrayList [1,+,(,(,2,+,3,),*,4,),-,5] = "ArrayList [1,2,3,+,4,*,+,5, –]
	//Method: List corresponding to infix expression = > List corresponding to suffix expression
	public static List<String> parseSuffixExpreesionList(List<String> ls) {
		//Define two stacks
		Stack<String> s1 = new Stack<String>(); // Symbol stack
		//Note: because s2 is a stack, there is no pop operation in the whole conversion process, and we need to output it in reverse order later
		//Therefore, it's troublesome. Here, we don't need stack < string > to directly use list < string > S2
		//Stack<String> s2 = new Stack<String>(); //  Stack S2 for storing intermediate results
		List<String> s2 = new ArrayList<String>(); // Lists2 for storing intermediate results
		
		//Traversal ls
		for(String item: ls) {
			//If it's a number, add s2
			if(item.matches("\\d+")) {
				s2.add(item);
			} else if (item.equals("(")) {
				s1.push(item);
			} else if (item.equals(")")) {
				//If it is the closing parenthesis ")", the operators at the top of s1 stack will pop up in turn and press s2 until the left parenthesis is encountered. At this time, this pair of parentheses will be discarded
				while(!s1.peek().equals("(")) {
					s2.add(s1.pop());
				}
				s1.pop();//!!!  Pop (out of s1 stack and eliminate parentheses
			} else {
				//When the priority of item is less than or equal to the top operator of s1 stack, pop up the top operator of s1 stack and add it to s2. Go to (4.1) again and compare it with the new top operator in s1
				//Problem: we lack a way to compare priorities
				while(s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item) ) {
					s2.add(s1.pop());
				}
				//You also need to push the item onto the stack
				s1.push(item);
			}
		}
		
		//Pop up the remaining operators in s1 and add s2
		while(s1.size() != 0) {
			s2.add(s1.pop());
		}

		return s2; //Note that because it is stored in the List, the output in order is the List corresponding to the corresponding suffix expression
		
	}
	
	//Method: convert infix expression to corresponding List
	//  s="1+((2+3)×4)-5";
	public static List<String> toInfixExpressionList(String s) {
		//Define a List to store the contents corresponding to infix expressions
		List<String> ls = new ArrayList<String>();
		int i = 0; //This is a pointer used to traverse the infix expression string
		String str; // Splicing of multi bit numbers
		char c; // Every time a character is traversed, it is put into c
		do {
			//If c is a non number, I need to add ls
			if((c=s.charAt(i)) < 48 ||  (c=s.charAt(i)) > 57) {
				ls.add("" + c);
				i++; //i need to move back
			} else { //If it is a number, multiple numbers need to be considered
				str = ""; //First set str to "" '0' [48] - [9 '[57]
				while(i < s.length() && (c=s.charAt(i)) >= 48 && (c=s.charAt(i)) <= 57) {
					str += c;//Splicing
					i++;
				}
				ls.add(str);
			}
		}while(i < s.length());
		return ls;//return
	}
	
	//Put an inverse Polish expression, and put the data and operators into the ArrayList in turn
	public static List<String> getListString(String suffixExpression) {
		//Split suffixExpression
		String[] split = suffixExpression.split(" ");
		List<String> list = new ArrayList<String>();
		for(String ele: split) {
			list.add(ele);
		}
		return list;
		
	}
	
	//Complete the operation of the inverse Polish expression
	/*
	 * 1)Scan from left to right and press 3 and 4 into the stack;
		2)Encounter the + operator, so pop up 4 and 3 (4 is the top element of the stack and 3 is the secondary top element), calculate the value of 3 + 4, get 7, and then put 7 on the stack;
		3)Put 5 into the stack;
		4)Next is × Operator, so pop up 5 and 7 and calculate 7 × 5 = 35, put 35 into the stack;
		5)Put 6 into the stack;
		6)Finally, the - Operator calculates the value of 35-6, i.e. 29, so as to obtain the final result
	 */
	
	public static int calculate(List<String> ls) {
		// To create a stack, you only need one stack
		Stack<String> stack = new Stack<String>();
		// Traversal ls
		for (String item : ls) {
			// Regular expressions are used here to extract numbers
			if (item.matches("\\d+")) { // The number of multiple bits matches
				// Push 
				stack.push(item);
			} else {
				// pop out two numbers, operate them, and then put them on the stack
				int num2 = Integer.parseInt(stack.pop());
				int num1 = Integer.parseInt(stack.pop());
				int res = 0;
				if (item.equals("+")) {
					res = num1 + num2;
				} else if (item.equals("-")) {
					res = num1 - num2;
				} else if (item.equals("*")) {
					res = num1 * num2;
				} else if (item.equals("/")) {
					res = num1 / num2;
				} else {
					throw new RuntimeException("Incorrect operator");
				}
				//Put res on the stack
				stack.push("" + res);
			}
			
		}
		//The last data left in the stack is the result of the operation
		return Integer.parseInt(stack.pop());
	}

}

//Writing a class Operation can return the priority corresponding to an operator
class Operation {
	private static int ADD = 1;
	private static int SUB = 1;
	private static int MUL = 2;
	private static int DIV = 2;
	
	//Write a method to return the corresponding priority number
	public static int getValue(String operation) {
		int result = 0;
		switch (operation) {
		case "+":
			result = ADD;
			break;
		case "-":
			result = SUB;
			break;
		case "*":
			result = MUL;
			break;
		case "/":
			result = DIV;
			break;
		default:
			System.out.println("The operator does not exist" + operation);
			break;
		}
		return result;
	}
	
}