1.Codeforces 961F k-substrings

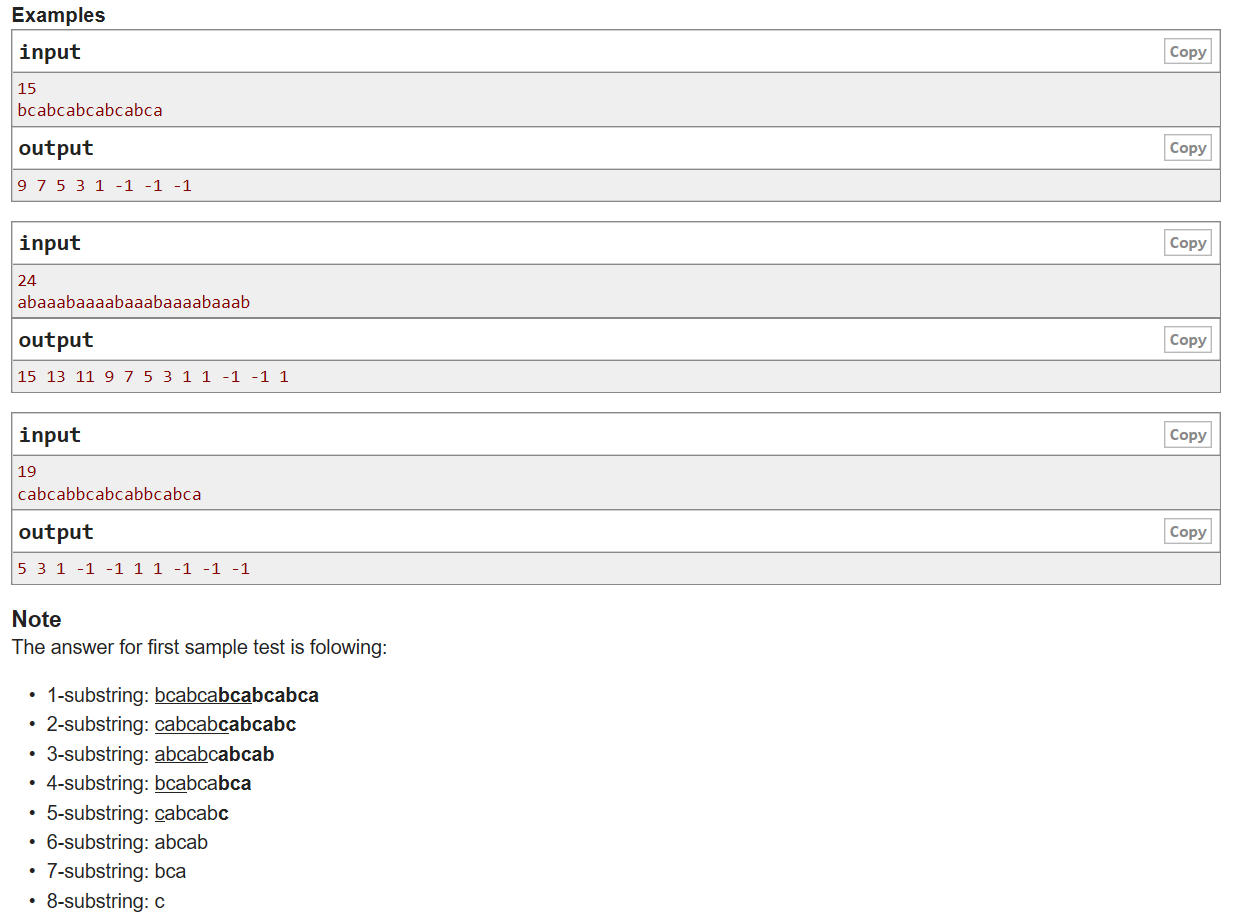
Main idea: given a string, for all its substrings    K − substrings    k-substrings\;k − substrings, ask its prefix and suffix the same maximum length, and the length must be odd, if not, then it is    1    \; - 1 \; - 1.    K − substrings    k-substrings\;k − substrings are defined as follows: for each string, delete    i   i\;i characters at the beginning and end of each string.

Design idea: for this problem, we consider using the string     Hash\;Hash to solve. First, consider the simple enumeration idea, that is, for a substring, enumerate all odd prefixes and suffixes from large to small, and then judge whether they are equal according to Hash value. In the worst case, the complexity will reach   O(n2)   O(n^2)\;O(n2), even if   4s   4s\;4s is not enough. Observe the characteristics of strings. When calculating the maximum common prefix and suffix of   I ⁩ i\;i, because each substring shrinks from two ends to the middle, there is such a result as   res[i] − 2 ≤ res[i+1]   res[i]-2 ≤ res[i+1]\;res[i] − 2 ≤ res[i+1], as shown in the following figure:

- 2. res[i+1]+2\;res[i] ≤ res[i+1]+2, the problem is just to find the maximum value. According to this equation, we can get the result + 2 of the longer substring that will not be shorter, so we start enumeration from the middle, and then for each substring, we start from the last result, step by step - 2, to judge whether the Hash value is equal.

Solution:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 5;
const ll base = 131;
const ll mod = 1e9 + 7;
ll Hash[maxn], b[maxn];
char ch[maxn];
int n, t, res[maxn / 2];
inline int read()
{
	int t = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9')
	{
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9')
	{
		t = (t << 3) + (t << 1) + (ch ^ 48);
		ch = getchar();
	}
	return t;
}
inline void write(int t)
{
	if (t < 0)
	{
		putchar('-');
		t = -t;
	}
	if (t > 9)
	{
		write(t / 10);
	}
	putchar(t % 10 + '0');
}
inline void init()
{
	b[0] = 1;
	for (int i = 1; i <= n; i++)
	{
		b[i] = (b[i - 1] * base) % mod;
	}
	for (int i = 1; i <= n; i++)
	{
		Hash[i] = (Hash[i - 1] * base + ch[i] - 'a' + 1) % mod;
	}
}
inline ll get_hash(int l, int r)
{
	return ((Hash[r] - Hash[l - 1] * b[r - l + 1]) % mod + mod) % mod;
}
inline void solve(int x)
{
	int y = t + t - x;
	if (!(n & 1))		//It's still a parity problem. When the number is even, the right boundary is + 1. You can find it by simple simulation
	{
		y++;
	}
	for (int i = res[x + 1] + 2; i >= 1; i -= 2)		//Enumeration from last result
	{
		if (get_hash(x, x + i - 1) == get_hash(y - i + 1, y))
		{
			res[x] = i;
			return;
		}
	}
	res[x] = -1;
	return;
}
int main()
{
	n = read();
	scanf("%s", ch + 1);
	init();
	t = n / 2;			//Deal with odd and even string length respectively
	if (n & 1)
	{
		t++;
		res[t] = -1;		//For an odd length string, the length at both ends is symmetric with respect to a character. The characters in the middle must have no prefix or suffix
	}
	else
	{
		if (ch[t] == ch[t + 1])		//Even length can be compared with the middle two characters
		{
			res[t] = 1;
		}
		else
		{
			res[t] = -1;
		}
	}
	for (int i = t - 1; i > 0; i--)
	{
		solve(i);		//Start enumeration from the middle, and then solve the longer substring
	}
	for (int i = 1; i <= t; i++)
	{
		write(res[i]);
		if (i == t)
		{
			putchar(10);
		}
		else
		{
			putchar(' ');
		}
	}
	return 0;
}

2.Codeforces 985F Isomorphic Strings

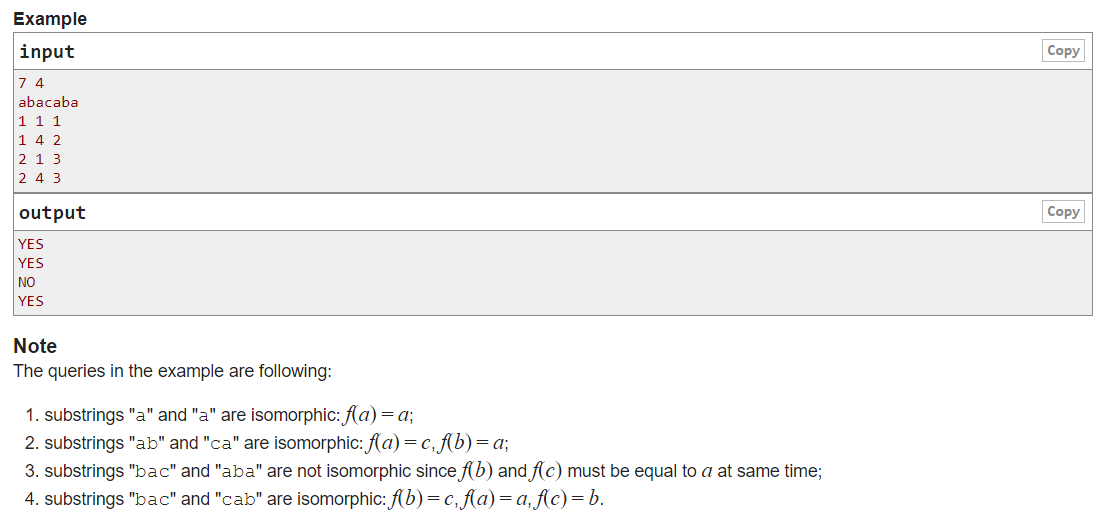
Main idea: given a string, and then every time cut off the equal length of the two strings, ask whether the two strings are isomorphic. (isomorphism is a relationship in which two characters are mapped one by one, that is, they cannot be many to one or one to many.)

Design idea: if we simply adopt the one-to-one mapping method to traverse each query substring, then the complexity will certainly not meet the needs. Because the question here is whether two strings can be isomorphic, and the string   Hash\;Hash \; Hash's idea is to map a string to a unique integer as far as possible, and judge whether two strings are equal by comparing two integers. Here, the relationship between the two strings is not only the corresponding characters are equal, but also to meet the special isomorphic relationship. Therefore, hash \; will not be used for strings at this time; Hash, and for the position of each character   Hash\;Hash \; hash, then determine whether it is isomorphic by the value of     \; Hash\;Hash.

How to understand the position    Hash    Hash\;Hash is the difficulty of this problem. First of all, we need to know that    Hash   Hash function has a similar prefix and property. Each character    Hash   Hash value is based on the result of the previous digit multiplied by the value of base plus the value of the base character. Now consider whether the two strings are isomorphic. Let's take a look at the following example;

For example, for the string    abcabbadbcc    abcabbadbcc \; abcabbadbcc, select its two substrings, such as    bcabb    bcabb\;bcabb and    cdbcc   cdbcc, the naked eye can see that these two strings are isomorphic, so how to use the computer to judge? In this example,    f(b)=c   ,    f(c)=d,f(a)=b  ; f(b)=c\;,\;f(c)=d,f(a)=b\;f(b)=c,f(c)=d,f(a)=b, that is to say, each letter has a corresponding relationship with another. With this idea, we consider mapping the original string to 26 01 strings, each 01 string represents a letter, and the position is that this character is 1 and the rest is 0. Then in the above example, we can convert it to 100100000, 010011000100, 00100001011, 000000001000 That is to say, for   B   b\;b and   C   c\;c. The one-to-one mapping is satisfied, because if the substring is A... A... And... C... C... C... , then the corresponding 01 string is 010... 010... And... 010... 010... 010... , these two strings must not be equal. Therefore, to determine whether the two strings are isomorphic, you only need to get the   Hash\;Hash of each letter of the two strings, and then determine whether there is a one-to-one correspondence between the 26 letters of the two strings.

Solution:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 6;
const ll base = 131;
const ll mod = 1e9 + 7;
int n, m;
char ch[maxn];
int x, y, len;
ll Hash[maxn][30], b[maxn];
inline int read()
{
	int t = 0;
	char ch = getchar();
	while (ch < '0' || ch>'9')
	{
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9')
	{
		t = (t << 3) + (t << 1) + (ch ^ 48);
		ch = getchar();
	}
	return t;
}
inline void init()
{
	b[0] = 1;
	for (int i = 1; i <= n; i++)
	{
		b[i] = (b[i - 1] * base) % mod;
	}
}
inline ll get_hash(int l, int r, int t)
{
	return (((Hash[r][t] - Hash[l - 1][t] * b[r - l + 1])) % mod + mod) % mod;
}
inline bool check()
{
	ll res_a[30], res_b[30];
	for (int i = 1; i <= 26; i++)		//Get 26 Hash values of two string pairs
	{
		res_a[i] = get_hash(x, x + len - 1, i);
		res_b[i] = get_hash(y, y + len - 1, i);
	}
	//Sort for comparison
	sort(res_a + 1, res_a + 27);
	sort(res_b + 1, res_b + 27);
	for (int i = 1; i <= 26; i++)
	{
		if (res_a[i] != res_b[i])
		{
			return false;
		}
	}
	return true;
}
int main()
{
	n = read();
	m = read();
	scanf("%s", ch + 1);
	init();
	//Convert the original string to 26 01 strings
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= 26; j++)
		{
			Hash[i][j] = (Hash[i - 1][j] * base % mod + (ll)(ch[i] == (j - 1 + 'a'))) % mod;
		}
	}
	while (m--)
	{
		x = read();
		y = read();
		len = read();
		if (check())
		{
			puts("YES");
		}
		else
		{
			puts("NO");
		}
	}
	return 0;
}

Have time to update the end of the flower!