The algorithm practice of data structure is for homework. I chose the traversal of the graph, because I feel that it will be more clear about the relevant algorithms than other topics. This article is written to make everyone more clear about the traversal algorithm of the graph, and also to review their relevant knowledge again, so as to help them pass the customs smoothly during their defense. I hope the defense is smooth!!! I also hope that the babies who see the article will be more clear about the traversal of the graph!! ❤
---------------

1, What is graph traversal

Traversal of a graph refers to starting from any vertex in the graph, accessing all vertices in the graph once and only once (accessing once, but using more than once). The traversal operation of a graph is similar to that of a tree (the traversal of the pre order, middle order and post order of a binary tree can also be considered as depth first traversal in essence, while the sequence traversal of a binary tree can also be considered as breadth first traversal in essence). Graph traversal is a basic operation of graph, and many other operations of graph are based on traversal operation.
For example, if you want to go shopping, there are many stores on the street, a,b,c,d,e,f,g. how can you browse them? If you use the traversal operation of our graph, you can arrange them through breadth first and depth first

So, after understanding what is graph traversal, let's understand what is breadth traversal and depth traversal
**

2, Breadth traversal

**
Breadth first search, also known as breadth first search, is called BFS for short.
It is a hierarchical search process. Each step forward may access a batch of vertices. It does not go back like depth first search, so it is not a recursive algorithm. In order to achieve layer by layer access, the algorithm must use an auxiliary queue to remember the next layer of the vertex being accessed.
In fact, his original intention is to traverse a node first, then traverse the surrounding nodes connected by that node, and then traverse node by node, repeating the cycle
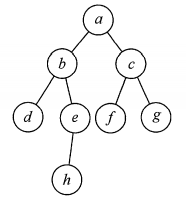
Do you remember the diagram of my example above? If you traverse according to breadth first, the access order is a, b, c, d, e, f, g and h.
It's traversing from the above layer to layer. This figure is in the style of binary tree, so it may be easier for you to understand. Now let's change to figure and do it together

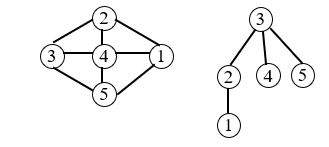
Then, for this graph, let's start traversing from "3" and use the breadth first method, then the traversal order we get is 3, 2, 3, 4, 5, 1;
**

3, Depth traversal

**
https://blog.csdn.net/qq_42024195/article/details/88350544?ops_request_misc=&request_id=&biz_id=102&utm_term=%E5%B9%BF%E5%BA%A6%E4%BC%98%E5%85%88%E9%81%8D%E5%8E%86&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-3-88350544.pc_search_result_control_group&spm=1018.2226.3001.4187
Here, I learned from the big guy's pictures, because I think the big guy's animation pictures are really great. From what I see, they are still very clear
First, the idea of the algorithm
Depth first search is similar to the prior traversal of a tree. The specific process is as follows:

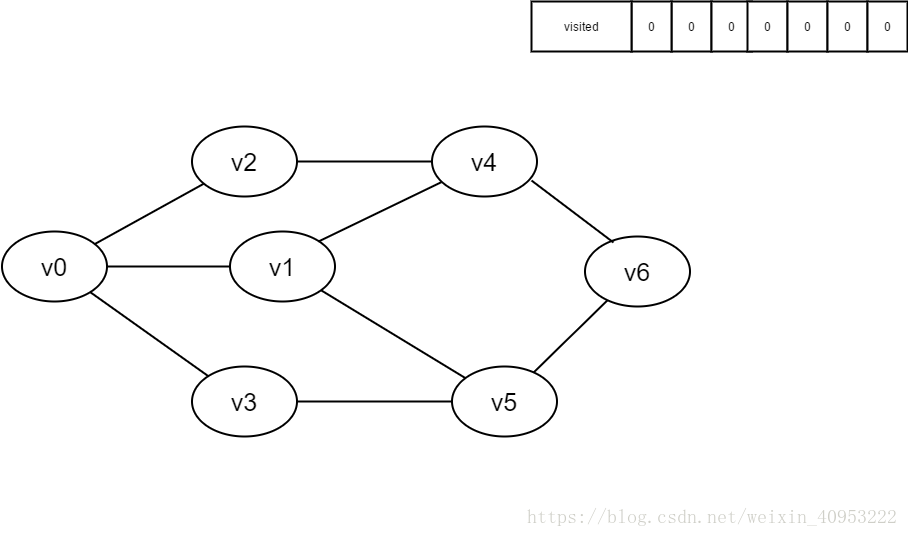
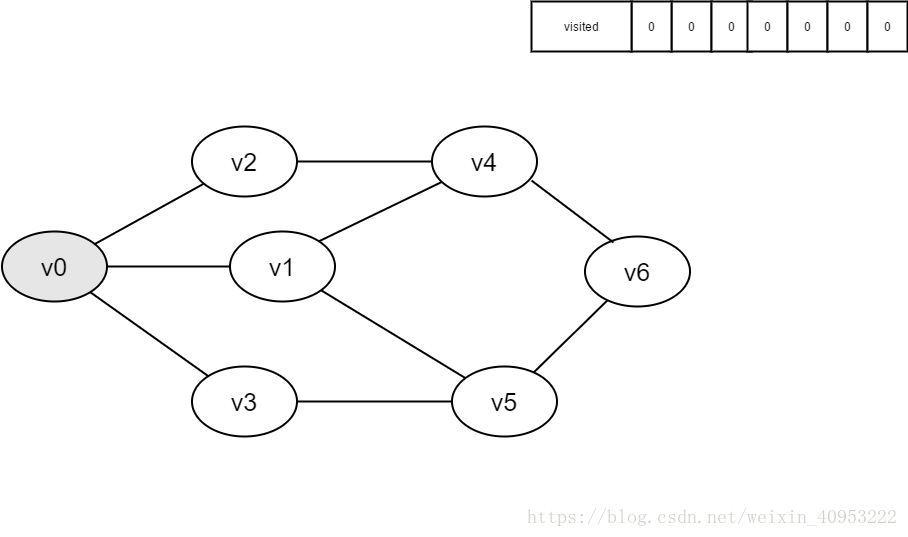
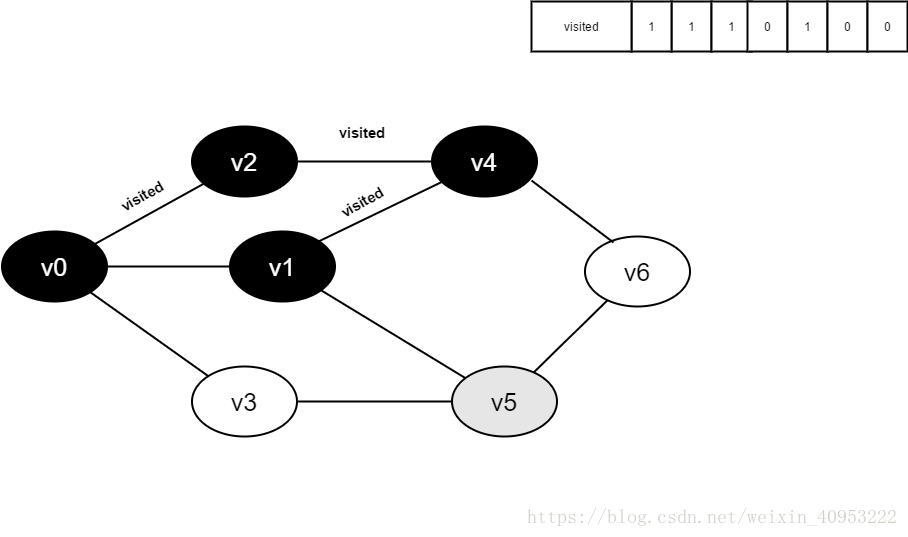
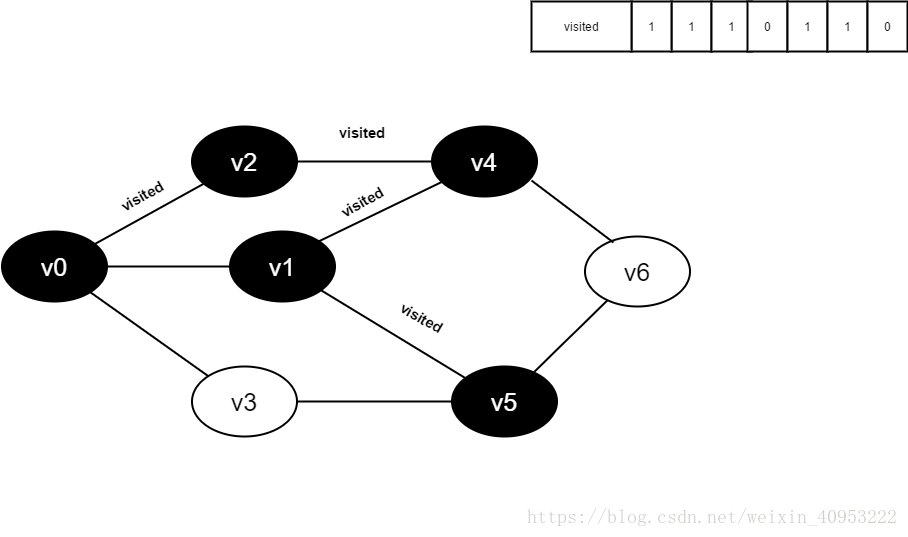
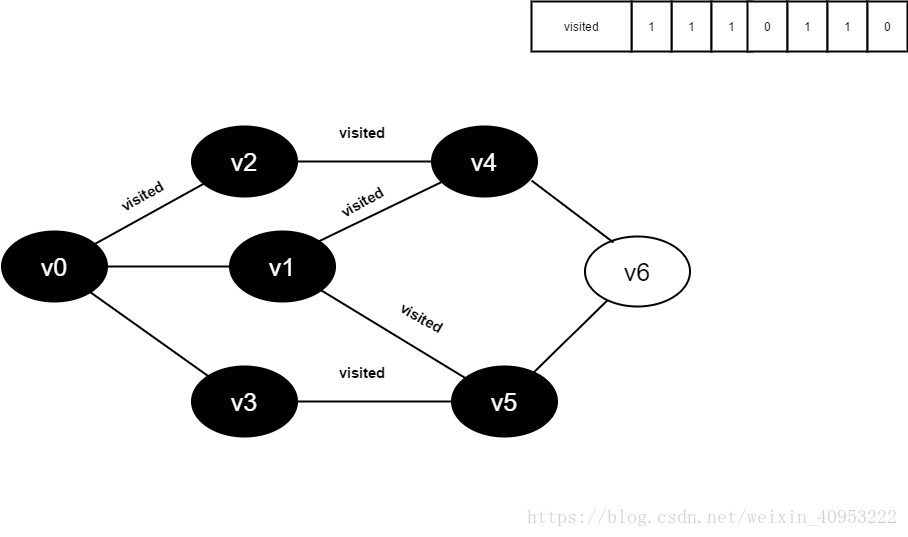
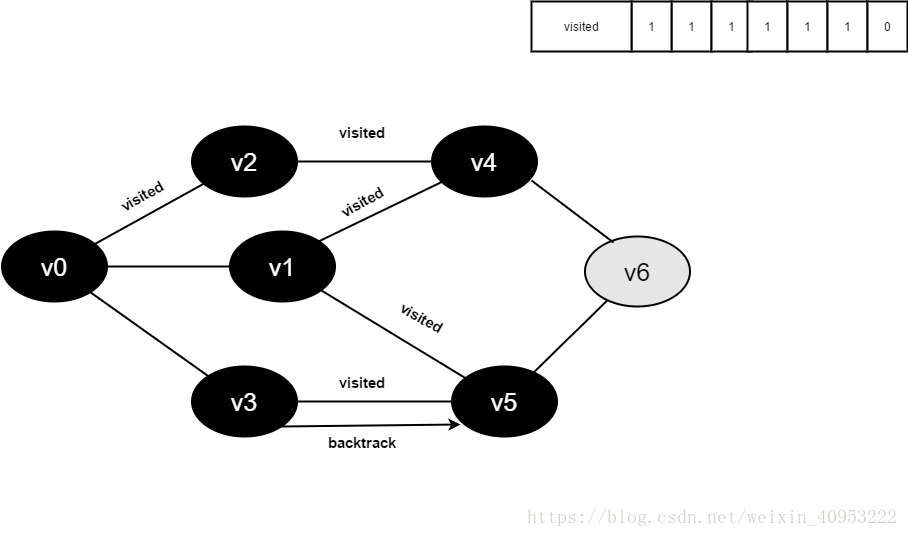
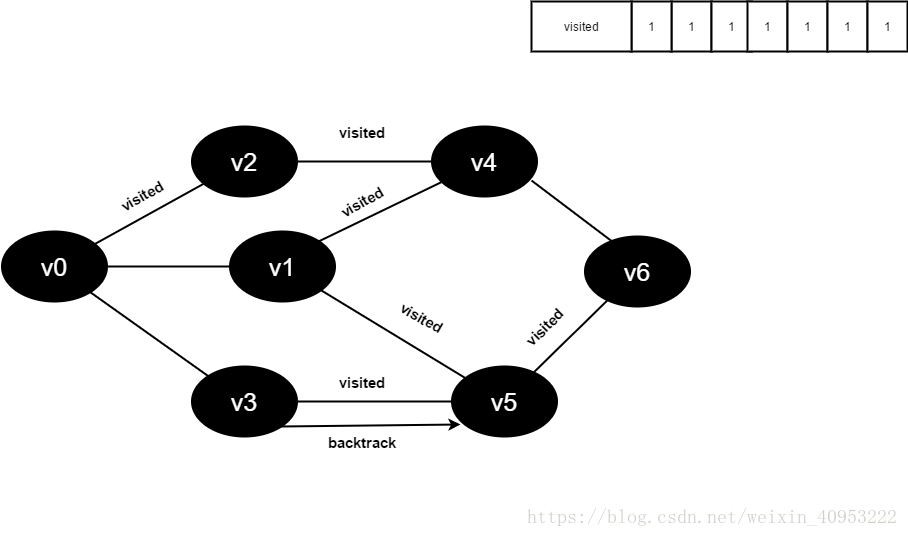
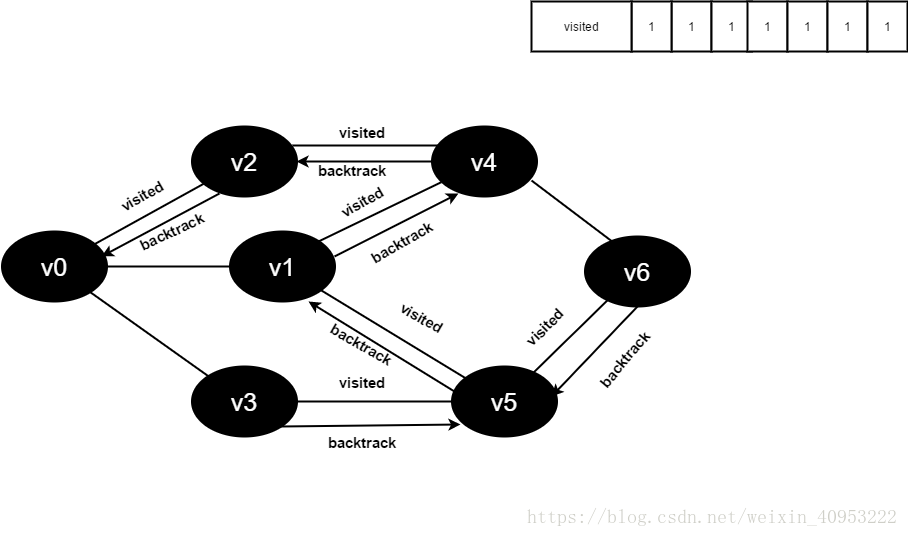
Preparation: create a visited array to record all accessed vertices.

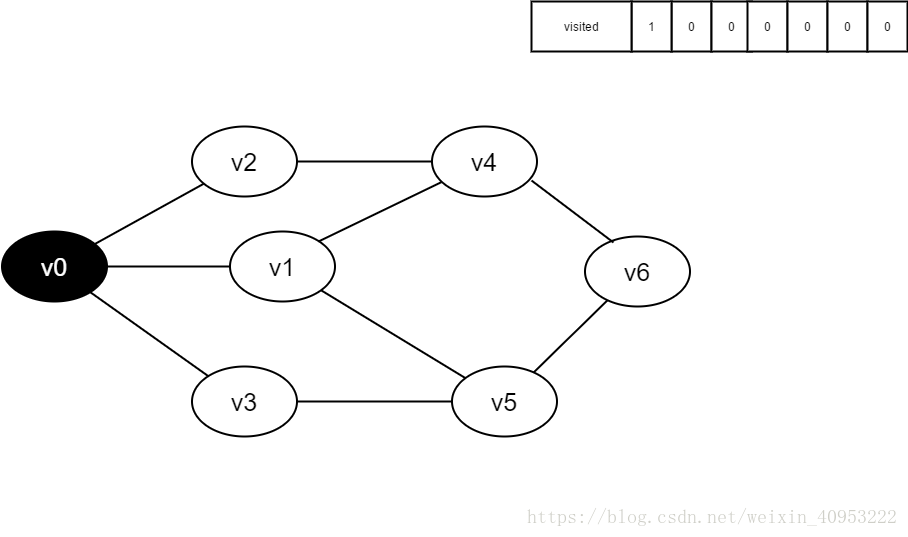
1. Start from V0 in the figure and visit v0.

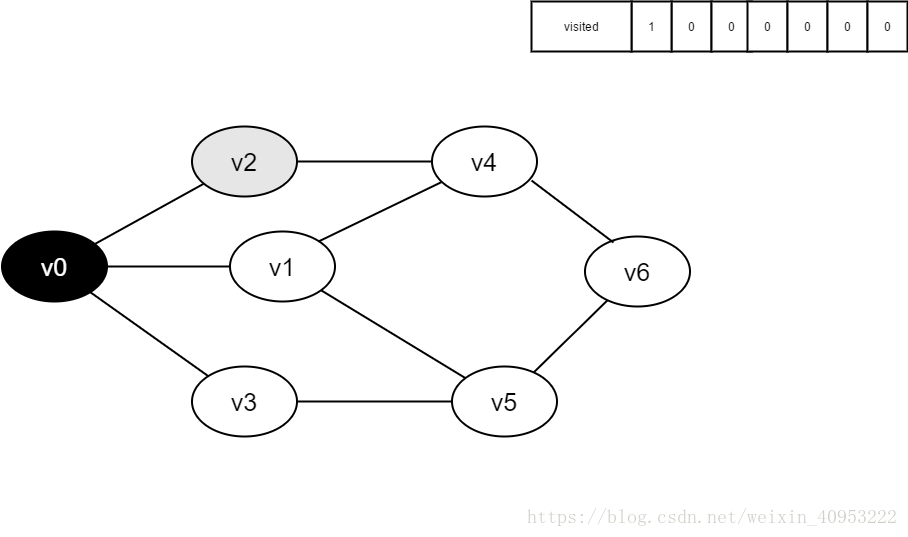
2. Find the first unreachable adjacency point of v0 and access the vertex. Take this vertex as a new vertex and repeat this step until the vertex just accessed has no adjacent points that are not accessed.

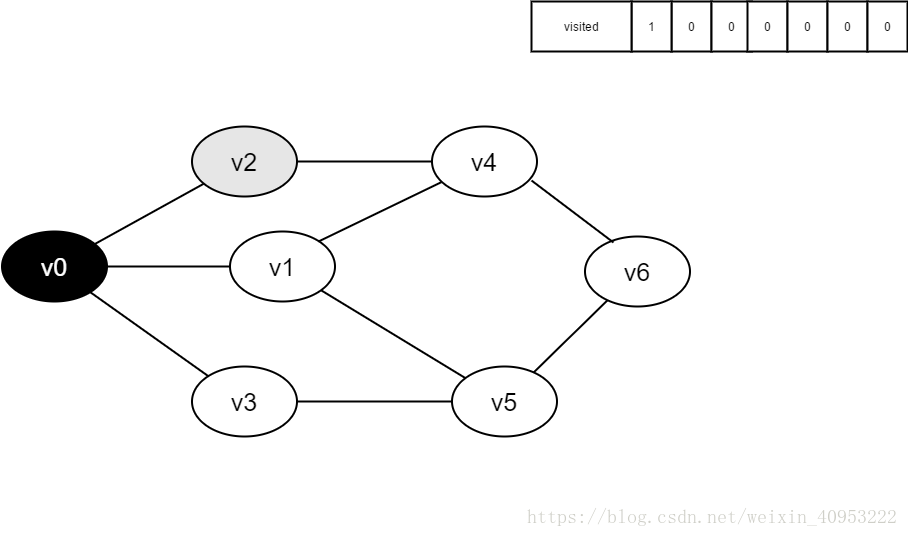
3. Return to the previously accessed vertex that still has an unreachable adjacency point, and continue to access the next unreachable collar point of the vertex.

4. Repeat steps 2 and 3 until all vertices are accessed and the search ends.















**

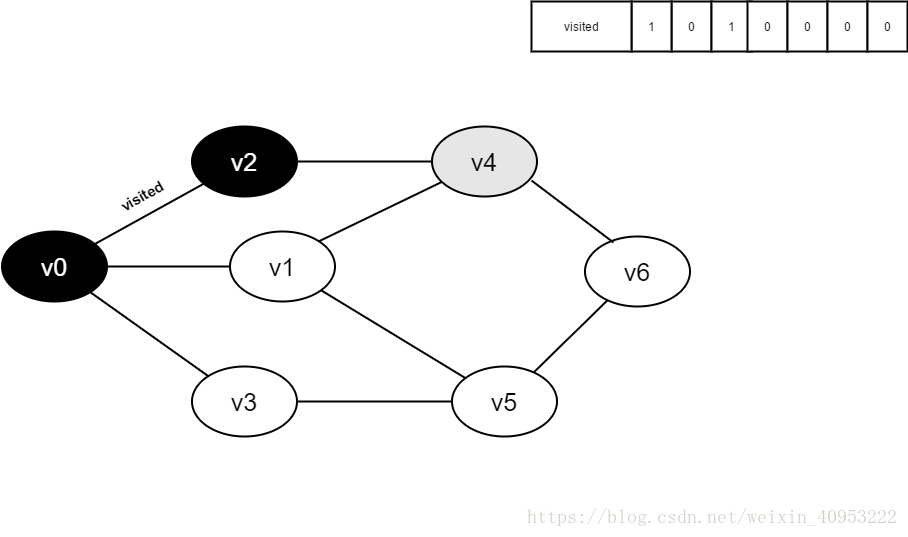
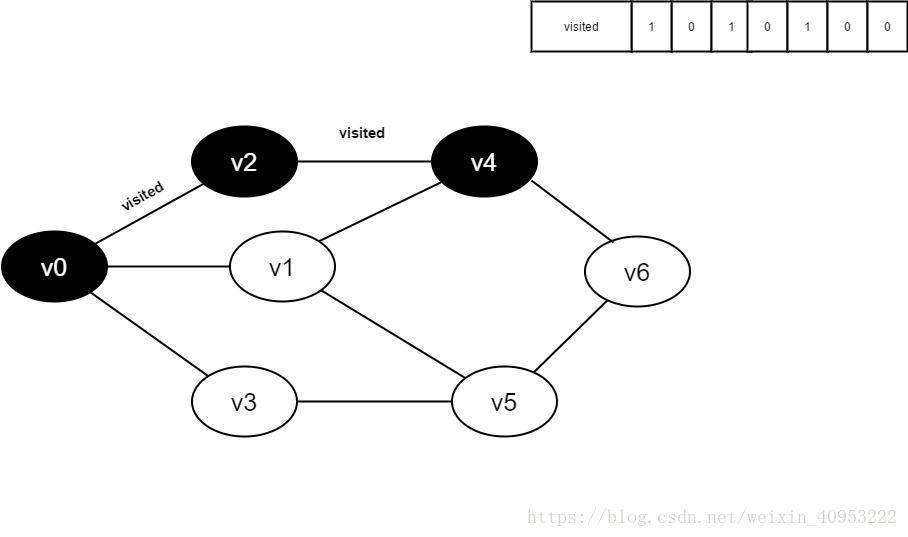
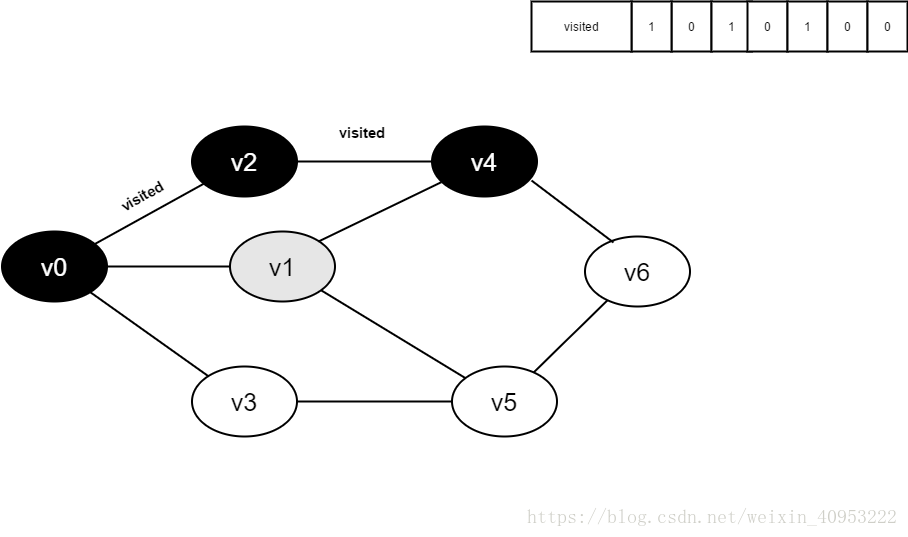
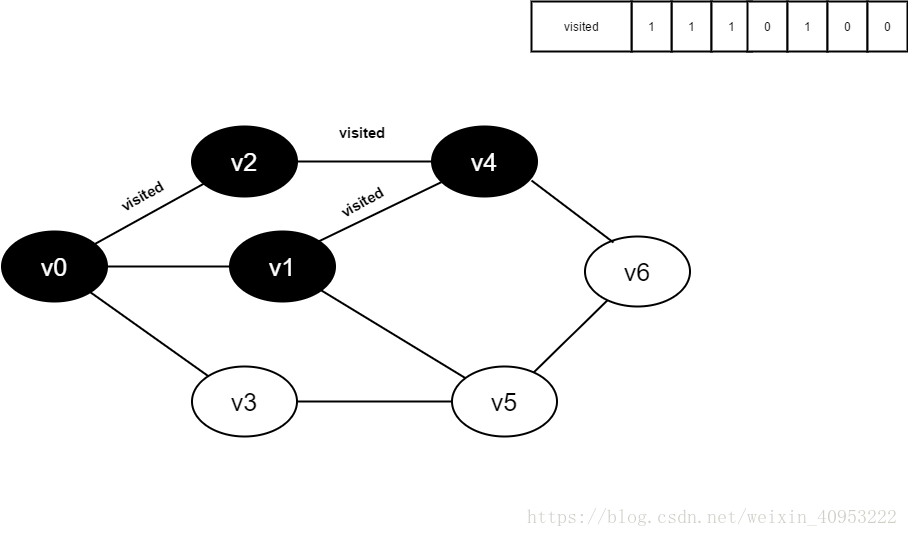
4, Code part

**

#include<stdio.h>
#include<stdlib.h>
#define max 20
typedef struct EdgeNode//Edge table node 
{   int adjvex;        //The subscript corresponding to the storage vertex stores a position rather than a specific element, which is convenient for changing data in the future 
	struct EdgeNode *next;//The chain domain points to the next adjacent node 
	int weight;      //Weight (if there is weight in the problem) 
}EdgeNode;
typedef struct VertexNode//Vertex table node 
{	char data;//Store vertex information 
	EdgeNode *firstedge;//Point to the first node in the edge table 
}VertexNode;
typedef struct
{	VertexNode adjlist[20];
	int n,e;
}GraphAdjlist;//Declare the adjacency table type of the graph 
int visited[10];//Access flag array (the accessed flag is assigned as 1, otherwise it is 0) 

void create(GraphAdjlist *G)//Create adjacency table 
{	int i,j,k;
	EdgeNode *e;
	printf("Please enter the number of vertices and edges:");
	scanf("%d%d",&G->n,&G->e);
	getchar();//Clear buffer 
	printf("Please enter the vertex edge number:\n");
	for(i=0;i<G->n;i++)
	{   scanf("%c",&G->adjlist[i].data);//Enter vertex number
		G->adjlist[i].firstedge=NULL;//Empty edge table 
		getchar(); 
	}
	for(k=0;k<G->e;k++)
	{   printf("Input edge( Vi,Vj)Vertex sequence number on:\n");
		scanf("%d%d",&i,&j);//The head interpolation method is convenient and fast. If the tail interpolation method needs the pointer to traverse to the tail, it is too slow 
		/*Adding edge table nodes using header interpolation*/
		e=(EdgeNode *)malloc(sizeof(EdgeNode));
		e->adjvex=j;
		e->next=G->adjlist[i].firstedge; 
		G->adjlist[i].firstedge=e;
		
		e=(EdgeNode *)malloc(sizeof(EdgeNode));//Because there are two vertices corresponding to one edge 
		e->adjvex=i;
		e->next=G->adjlist[j].firstedge; 
		G->adjlist[j].firstedge=e;	
	 } 
	printf("\n");
}
void DFS(GraphAdjlist *G,int i)
{	EdgeNode *p;
	visited[i]=1;
	printf("%c ",G->adjlist[i].data);
	p=G->adjlist[i].firstedge;
	while(p!=NULL)
	{	if(visited[p->adjvex]==0)
		  DFS(G,p->adjvex);
		p=p->next;
	}
}
void DFSTraverse(GraphAdjlist *G)
{	int i;
	for(i=0;i<G->n;i++)
	  visited[i]=0;
	for(i=0;i<G->n;i++)
	  if(visited[i]==0)
	    DFS(G,i);
}
void BFS(GraphAdjlist *G,int v)
{	EdgeNode *p;
	int queue[max],front=0,rear=0;//Define a circular queue and initialize it 
	int w,i;
	for(i=0;i<G->n;i++)//Flag array initialization 
	    visited[i]=0;
	printf("%2c",G->adjlist[v].data);
	visited[v]=1;
	rear=(rear+1)%max;
	queue[rear]=v;
	while(front!=rear)
	{	front=(front+1)%max;
		w=queue[front];
		p=G->adjlist[w].firstedge;
		while(p!=NULL)
		{	if(visited[p->adjvex]==0)
			{	printf("%2c",G->adjlist[p->adjvex].data);
				visited[p->adjvex]=1;
				rear=(rear+1)%max;
				queue[rear]=p->adjvex;
			}
			p=p->next;
		}
	}
	printf("\n");
}
int main()//A B C D E
{	GraphAdjlist G;
	create(&G);
	printf("Depth first traversal:");
	DFSTraverse(&G);
		printf("Breadth first traversal:");
	BFS(&G,0); 
	return 0;
}

I'm going to reply tomorrow, so I'm in a hurry. I don't have much time. Let's make do first. I'll make up after the reply