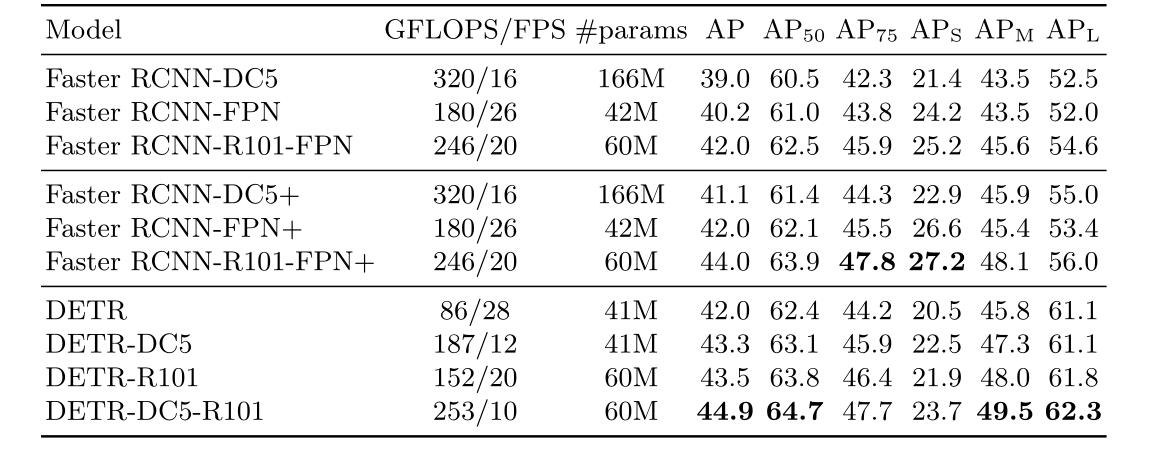
Features: self attention layers, end-to-end set predictions, bipartite matching loss
The DETR model has two important parts:
1) A set prediction loss that ensures a unique match between the real value and the predicted value.
2) An architecture that can predict (one-time) target sets and model their relationships.
3) Due to the addition of self attention mechanism, and in the process of learning, the audience's attention training is very good, and everyone's concerns are different, so the segmentation effect is very good and effectively solve the occlusion problem



DETR regards the target detection task as an image to set problem, that is, given an image, the prediction result of the model is an unordered set containing all targets.
This task transforms the target detection task into a set prediction task. Using the transformer codec structure and bilateral matching method, the prediction result sequence is directly obtained from the input image It does not generate anchor, but directly generates prediction structure
Disadvantages: it is poor for small target and multi-target scenes
1. Basic knowledge
1.1 one hot matrix: it refers to a matrix in which each row has one and only one element is 1 and other elements are 0. For each word in the dictionary, we assign a number. When encoding a sentence, we can convert each word into a one hot matrix with the corresponding position of 1 in the dictionary. For example, we want to express "the cat sat on the mat", which can be expressed by the following matrix.
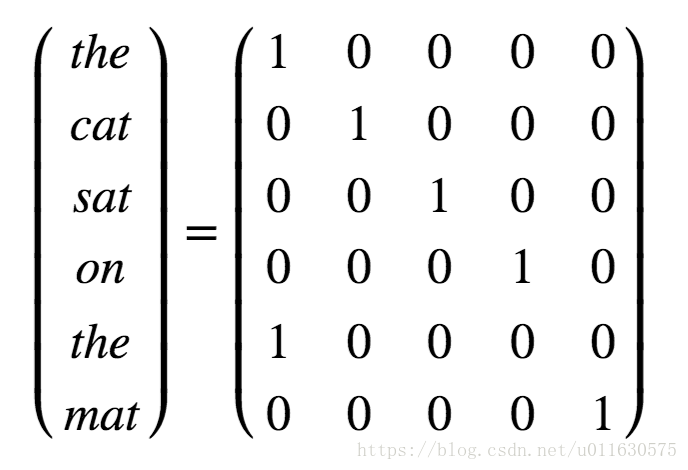
The one hot representation is very intuitive, but it has two disadvantages. First, the length of each dimension of the matrix is the length of the dictionary. For example, if the dictionary contains 10000 words, the one hot vector corresponding to each word is a 1X10000 vector, and only one position of this vector is 1, and the rest are 0, which wastes space and is not conducive to calculation. Second, the one hot matrix is equivalent to simply numbering each word, but the relationship between words can not be reflected at all. For example, the relevance of "cat" and "mouse" is higher than that of "cat" and "cell phone", which is not reflected in the one hot representation.
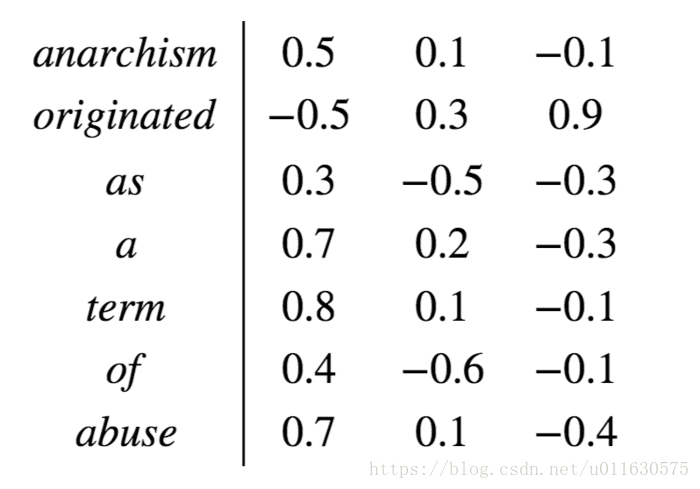
1.2 Word Embedding vector Word Embedding: solves these two problems. The Word Embedding matrix assigns a fixed length vector representation to each word. This length can be set by itself, such as 300, which is actually much smaller than the dictionary length (such as 10000). And the angle between two word vectors can be used as a measure of their relationship. As follows
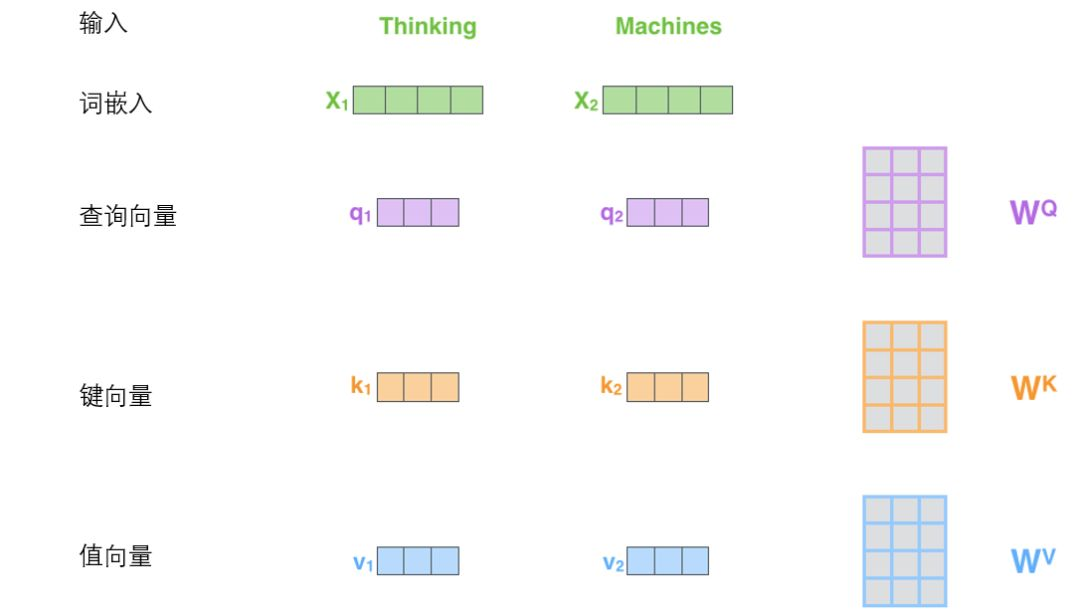
The three w matrices are the matrices to measure qkv weight. The weight matrices are all trained. The first step of self attention is to generate three vectors from the input vector of each encoder (the word vector of each word). That is, for each word, we create a query vector, a key vector and a value vector. These three vectors are created by word embedding and multiplying with three weight matrices.
Query vector: the embedded vector of each word is multiplied by the WQ vector. Used to multiply all key vectors to get scores directly.
Key vector: similarly, each word is embedded into the vector and W K.
Value vector: ditto. Used to weight the score of each word.
1.3 calculation steps of self attention:
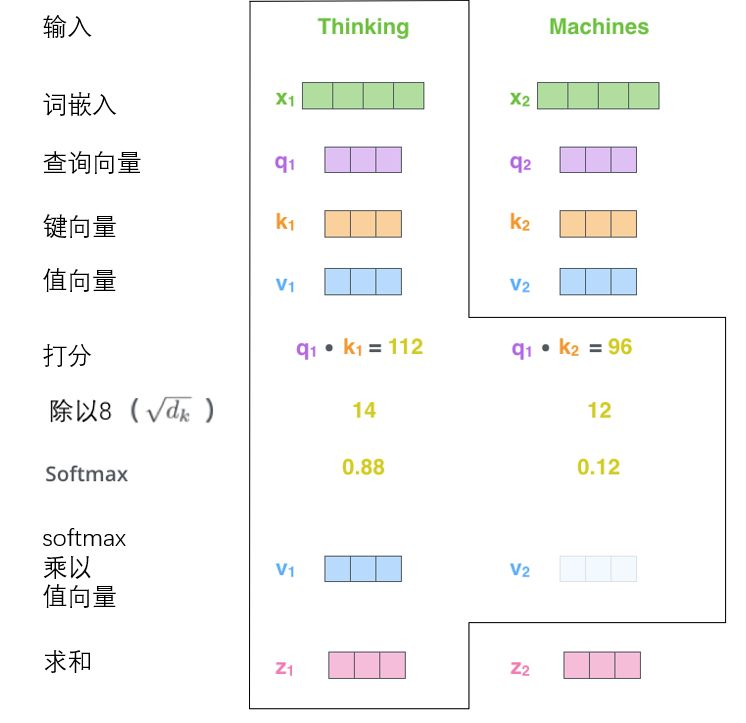
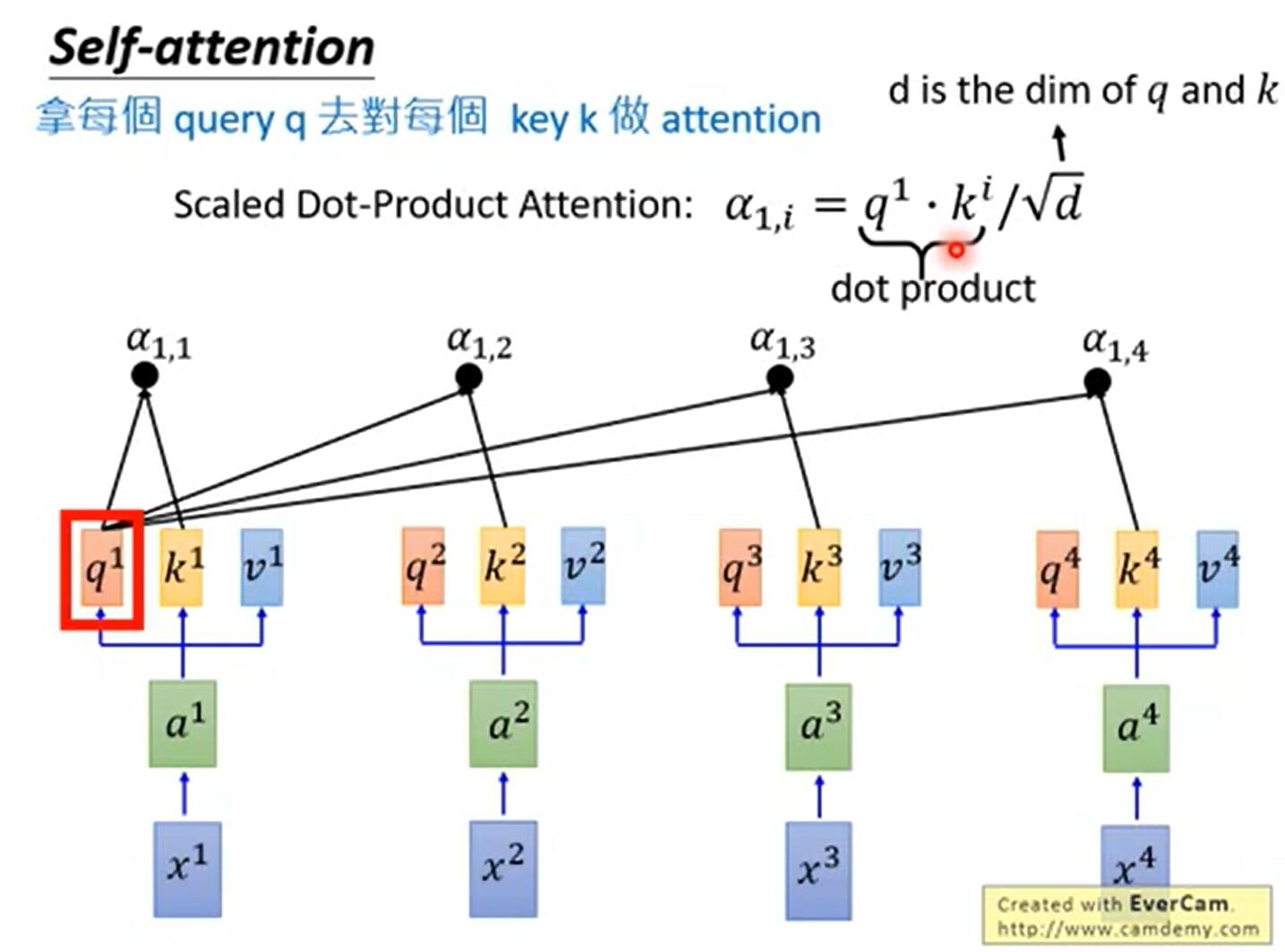
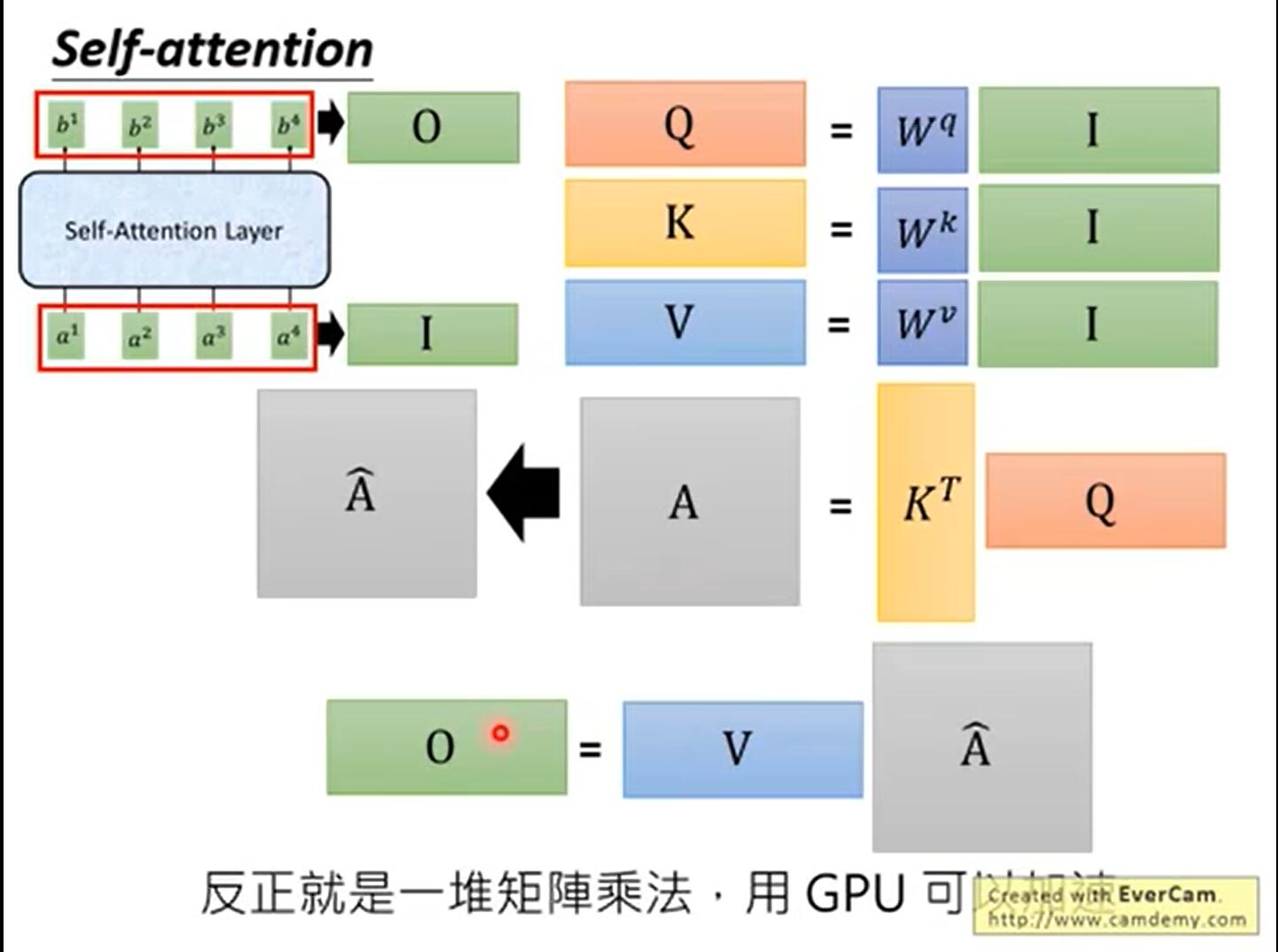
1. Multiply the query vector by each key vector to get a score, such as 112 and 96. This score evaluates the relevance of Thinking and Machines to themselves and other words.
2. Divide the score by the square root of the dimension of the key vector (sqrt{64}=8), and the dimension penalty item, which is conducive to the stability of the gradient.
3. Normalize softmax and get a weight for each word.
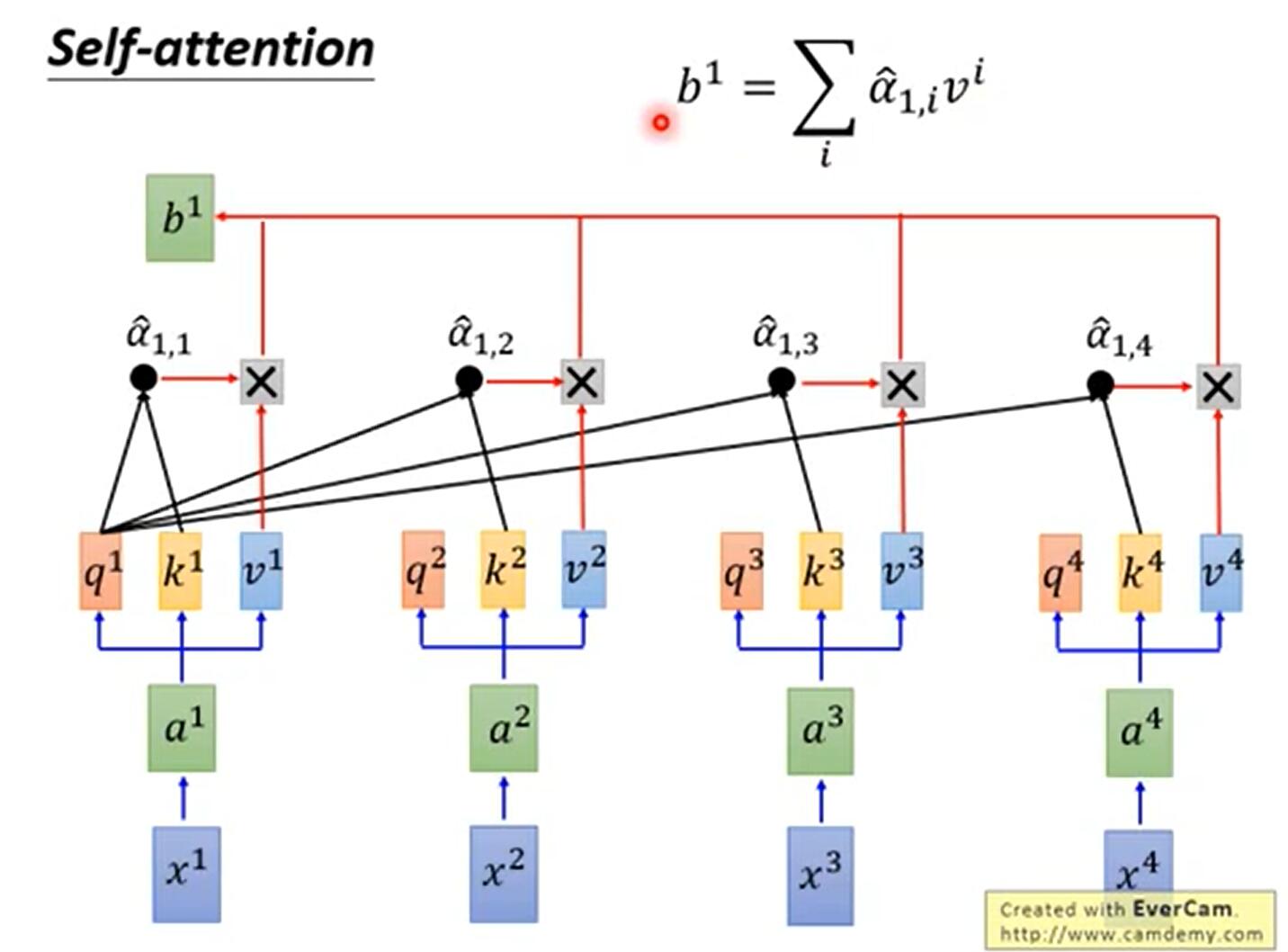
4. Weighted sum each value vector according to the weight of each word. Get Z i
bi is a variable that gathers global information. As long as it only counts (1,1) at Σ, it only collects local information.
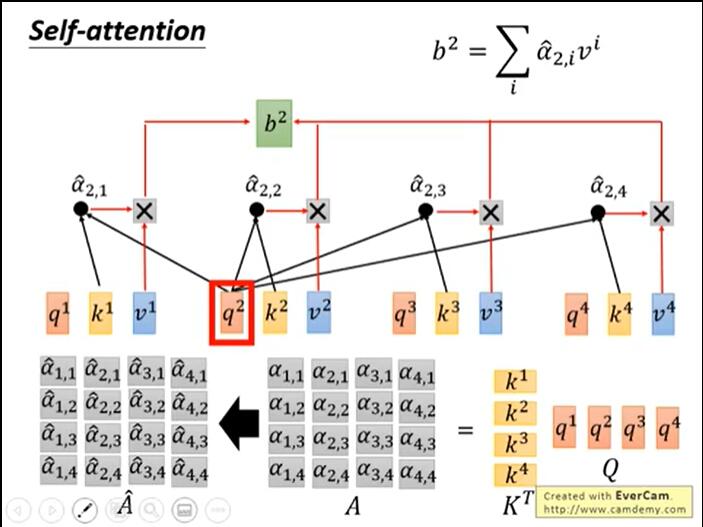
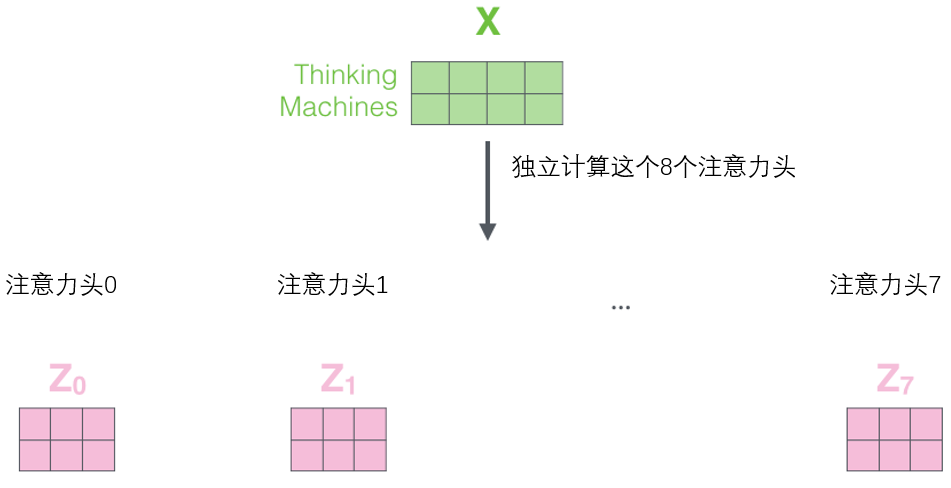
1.4 multi head self attention: for the "multi head" attention mechanism, we have multiple query / key / value weight matrix sets (Transformer uses eight attention heads, so we have eight matrix sets for each encoder / decoder). Each of these sets is randomly initialized, and after training, each set is used to project input words embedded (or vectors from lower encoders / decoders) into different representation subspaces
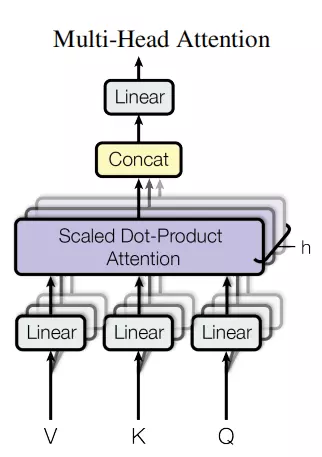
Then give eight matrices to concat, and then a training number matrix w0 to give him fusion attention
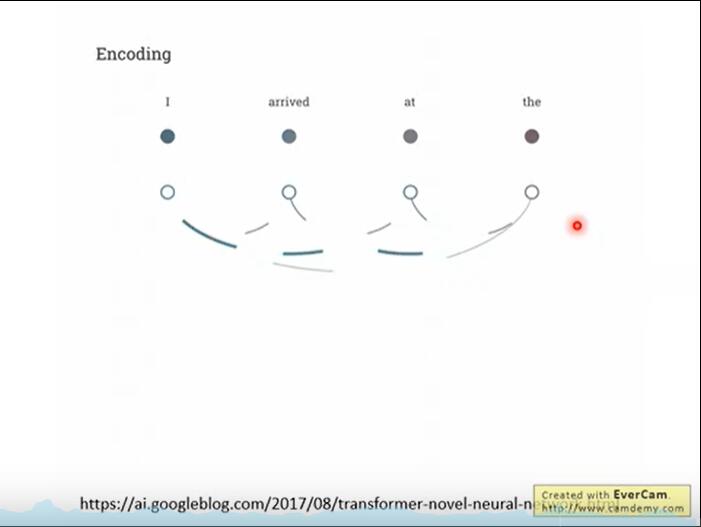
1.5 position encoding:
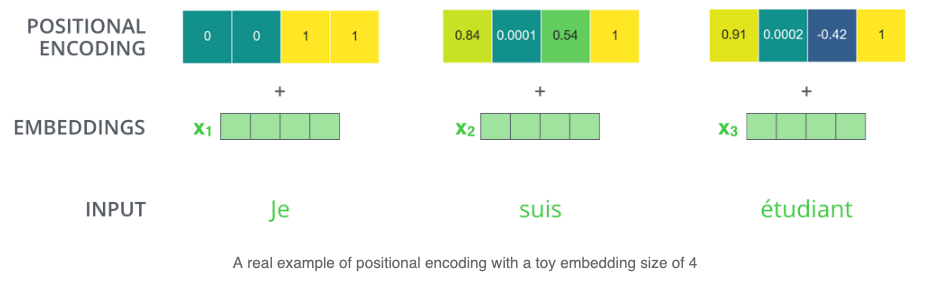
In NLP, words in sentences also need a location code to establish the distance between words. The encoder adds a vector for each input embedding, which conforms to a specific pattern and can determine the position of each word or the distance between different words in the sequence. For example, if the dimension of input embedding is 4, the actual positive encodings are as follows:
1. The author's own thoughts in the code
Arg:A set of super parameters Namespace(aux_loss=True, backbone='resnet50', batch_size=2, bbox_loss_coef=5, clip_max_norm=0.1, coco_panoptic_path=None, coco_path=None, dataset_file='coco', dec_layers=6, device='cuda', dice_loss_coef=1, dilation=False, dim_feedforward=2048, dist_url='env://', distributed=False, dropout=0.1, enc_layers=6, eos_coef=0.1, epochs=300, eval=False, frozen_weights=None, giou_loss_coef=2, hidden_dim=256, lr=0.0001, lr_backbone=1e-05, lr_drop=200, mask_loss_coef=1, masks=False, nheads=8, num_queries=100, num_workers=2, output_dir='', position_embedding='sine', pre_norm=False, remove_difficult=False, resume='', seed=42, set_cost_bbox=5, set_cost_class=1, set_cost_giou=2, start_epoch=0, weight_decay=0.0001, world_size=1)
A new data type created by the author is used to store features: tensor is the value of our pictures. When the pictures in a batch are different in size, we should deal with them neatly. In short, we should pad the pictures to the maximum size. The way of padding is to fill in zeros. Then each picture in the batch has a mask matrix, A mask matrix is used to indicate which are real data and which are padding, and 1 represents real data; 0 represents padding data.
NestedTensor Data type:
#NestedTensor, which consists of:
- samples.tensor: batched images, of shape [batch_size x 3 x H x W]
- samples.mask: a binary mask of shape [batch_size x H x W], containing 1 on padded pixels
class NestedTensor(object):
def __init__(self, tensors, mask: Optional[Tensor]):
self.tensors = tensors
self.mask = mask
def to(self, device):
# type: (Device) -> NestedTensor # noqa
cast_tensor = self.tensors.to(device)
mask = self.mask
if mask is not None:
assert mask is not None
cast_mask = mask.to(device)
else:
cast_mask = None
return NestedTensor(cast_tensor, cast_mask)
def decompose(self):
return self.tensors, self.mask
def __repr__(self):
return str(self.tensors)
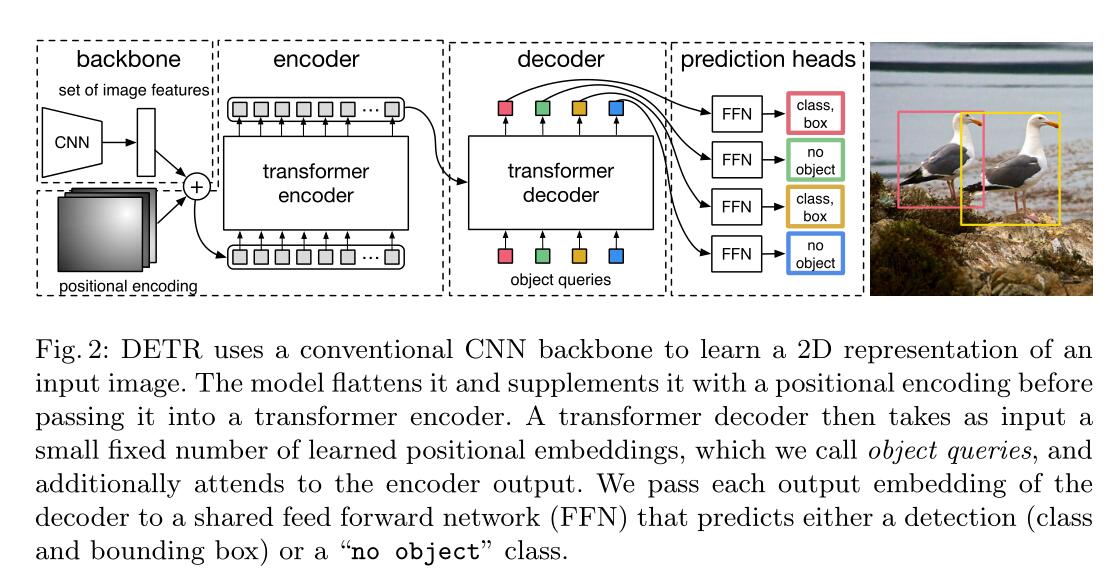
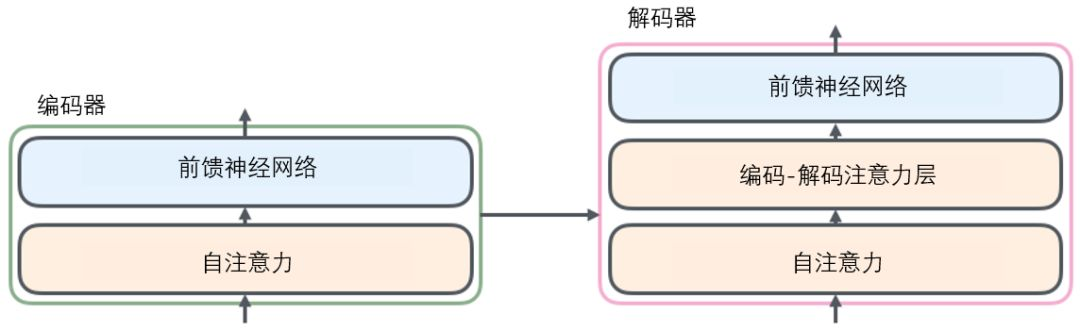
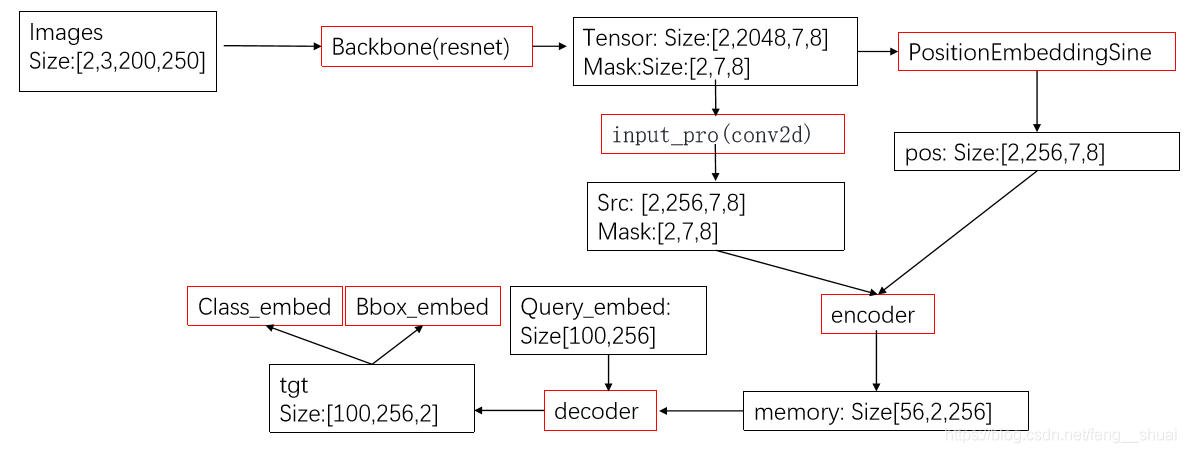
2.DETR network structure
detr did not propose a new layer, but directly proposed a new framework. First pass through the traditional cnn to extract features, and then conduct positive encoding at the same time. After the encoder and decoder of Transformer, the results are obtained through simple forward propagation network (FNN).
class DETR(nn.Module): def __init__(self, num_classes, hidden_dim, nheads, num_encoder_layers, num_decoder_layers): super().__init__() # We take only convolutional layers from ResNet-50 model self.backbone = nn.Sequential(*list(resnet50(pretrained=True).children())[:-2]) self.conv = nn.Conv2d(2048, hidden_dim, 1) self.transformer = nn.Transformer(hidden_dim, nheads, num_encoder_layers, num_decoder_layers) self.linear_class = nn.Linear(hidden_dim, num_classes + 1) self.linear_bbox = nn.Linear(hidden_dim, 4) self.query_pos = nn.Parameter(torch.rand(100, hidden_dim)) self.row_embed = nn.Parameter(torch.rand(50, hidden_dim // 2)) self.col_embed = nn.Parameter(torch.rand(50, hidden_dim // 2)) def forward(self, inputs): x = self.backbone(inputs) h = self.conv(x) H, W = h.shape[-2:] pos = torch.cat([ self.col_embed[:W].unsqueeze(0).repeat(H, 1, 1), self.row_embed[:H].unsqueeze(1).repeat(1, W, 1), ], dim=-1).flatten(0, 1).unsqueeze(1) h = self.transformer(pos + h.flatten(2).permute(2, 0, 1), self.query_pos.unsqueeze(1)) return self.linear_class(h), self.linear_bbox(h).sigmoid()
2.0backbone
His requirements are relatively simple, as long as they are met
The input is C=3 × H × W. The outputs are C = 2048 and h, W = H / 32, W / 32.
After that, all feature map s are flattened and turned into CxWH scale. At this time, the location information is two-dimensional
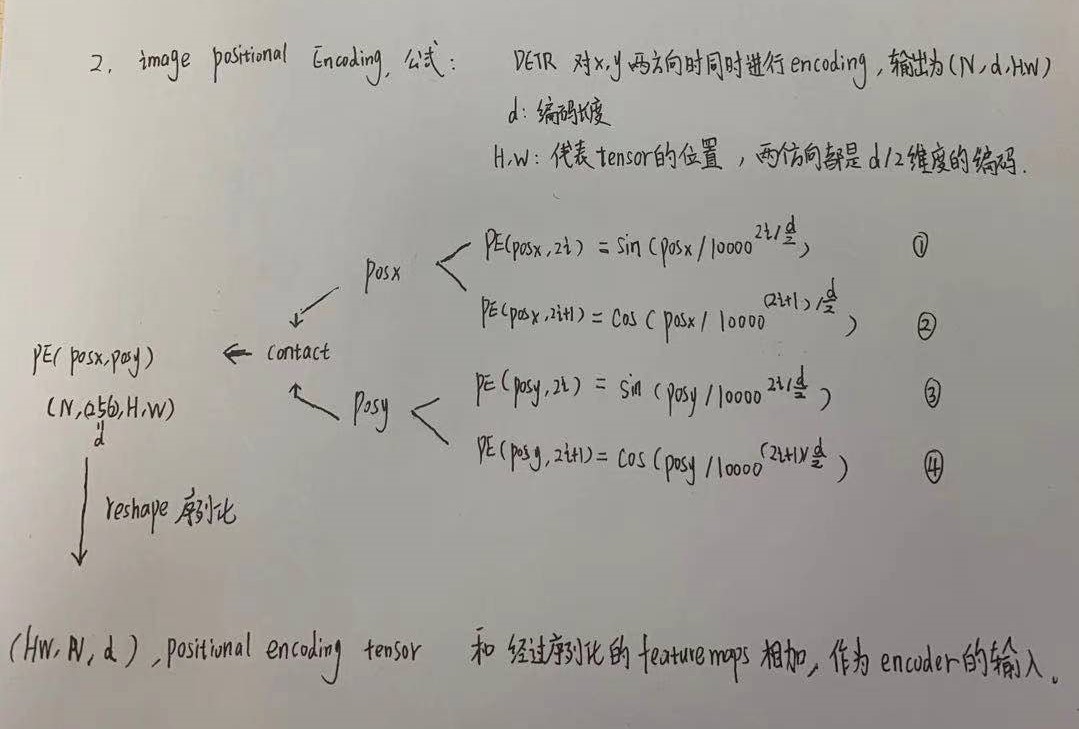
2.1position encode
Main.py:
def main(args):
model, criterion, postprocessors = build_model(args)
if __name__ == '__main__':
parser = argparse.ArgumentParser('DETR training and evaluation script', parents=[get_args_parser()])
args = parser.parse_args()
if args.output_dir:
Path(args.output_dir).mkdir(parents=True, exist_ok=True)
main(args)
Detr.py:
def build(args):
backbone = build_backbone(args)
position encoding:
def build_position_encoding(args):
N_steps = args.hidden_dim // 2# hide half of the layer dimension
if args.position_embedding in ('v2', 'sine'):
# TODO find a better way of exposing other arguments
position_embedding = PositionEmbeddingSine(N_steps, normalize=True)
elif args.position_embedding in ('v3', 'learned'):
position_embedding = PositionEmbeddingLearned(N_steps)
else:
raise ValueError(f"not supported {args.position_embedding}")
return position_embedding
class PositionEmbeddingSine(nn.Module):
"""
This is a more standard version of the position embedding, very similar to the one
used by the Attention is all you need paper, generalized to work on images.Made a peace Attention is all you need paper Same location coding
"""
def __init__(self, num_pos_feats=64, temperature=10000, normalize=False, scale=None):
super().__init__()
self.num_pos_feats = num_pos_feats
self.temperature = temperature
self.normalize = normalize
if scale is not None and normalize is False:
raise ValueError("normalize should be True if scale is passed")
if scale is None:
scale = 2 * math.pi
self.scale = scale
def forward(self, tensor_list: NestedTensor):
x = tensor_list.tensors
mask = tensor_list.mask
assert mask is not None
not_mask = ~mask
y_embed = not_mask.cumsum(1, dtype=torch.float32)
x_embed = not_mask.cumsum(2, dtype=torch.float32)
if self.normalize:
eps = 1e-6
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
pos_x = x_embed[:, :, :, None] / dim_t#The x - embed ded here is posx
pos_y = y_embed[:, :, :, None] / dim_t
pos_x = ((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
return pos
2.2Transform
class Transformer(nn.Module):
def __init__(self, d_model=512, nhead=8, num_encoder_layers=6,
num_decoder_layers=6, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False,
return_intermediate_dec=False):
super().__init__()
encoder_layer = TransformerEncoderLayer(d_model, nhead, dim_feedforward,
dropout, activation, normalize_before)
encoder_norm = nn.LayerNorm(d_model) if normalize_before else None
self.encoder = TransformerEncoder(encoder_layer, num_encoder_layers, encoder_norm)
#Six self coding: each time it is eight head self attention + FFN
decoder_layer = TransformerDecoderLayer(d_model, nhead, dim_feedforward,
dropout, activation, normalize_before)
decoder_norm = nn.LayerNorm(d_model)
self.decoder = TransformerDecoder(decoder_layer, num_decoder_layers, decoder_norm,
return_intermediate=return_intermediate_dec)
self._reset_parameters()
self.d_model = d_model
self.nhead = nhead
def _reset_parameters(self):
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
def forward(self, src, mask, query_embed, pos_embed):
# flatten NxCxHxW to HWxNxC
bs, c, h, w = src.shape
src = src.flatten(2).permute(2, 0, 1)
pos_embed = pos_embed.flatten(2).permute(2, 0, 1)
query_embed = query_embed.unsqueeze(1).repeat(1, bs, 1)#Expand into two channels, and the new layer is copied
mask = mask.flatten(1)#to pave nicely
tgt = torch.zeros_like(query_embed)#Output a size and query_ The same as embedded but all 0 matrices are initialized as the first layer fixed input at the beginning
memory = self.encoder(src, src_key_padding_mask=mask, pos=pos_embed)#code
hs = self.decoder(tgt, memory, memory_key_padding_mask=mask,
pos=pos_embed, query_pos=query_embed)#decode
return hs.transpose(1, 2), memory.permute(1, 2, 0).view(bs, c, h, w)
class PositionEmbeddingLearned(nn.Module):
"""
Absolute pos embedding, learned.
"""
def __init__(self, num_pos_feats=256):
super().__init__()
self.row_embed = nn.Embedding(50, num_pos_feats)
self.col_embed = nn.Embedding(50, num_pos_feats)
self.reset_parameters()
def reset_parameters(self):
nn.init.uniform_(self.row_embed.weight)
nn.init.uniform_(self.col_embed.weight)
def forward(self, tensor_list: NestedTensor):
x = tensor_list.tensors
h, w = x.shape[-2:]
i = torch.arange(w, device=x.device)
j = torch.arange(h, device=x.device)
x_emb = self.col_embed(i)
y_emb = self.row_embed(j)
pos = torch.cat([
x_emb.unsqueeze(0).repeat(h, 1, 1),
y_emb.unsqueeze(1).repeat(1, w, 1),
], dim=-1).permute(2, 0, 1).unsqueeze(0).repeat(x.shape[0], 1, 1, 1)
return pos
2.2.1Transformer encoder
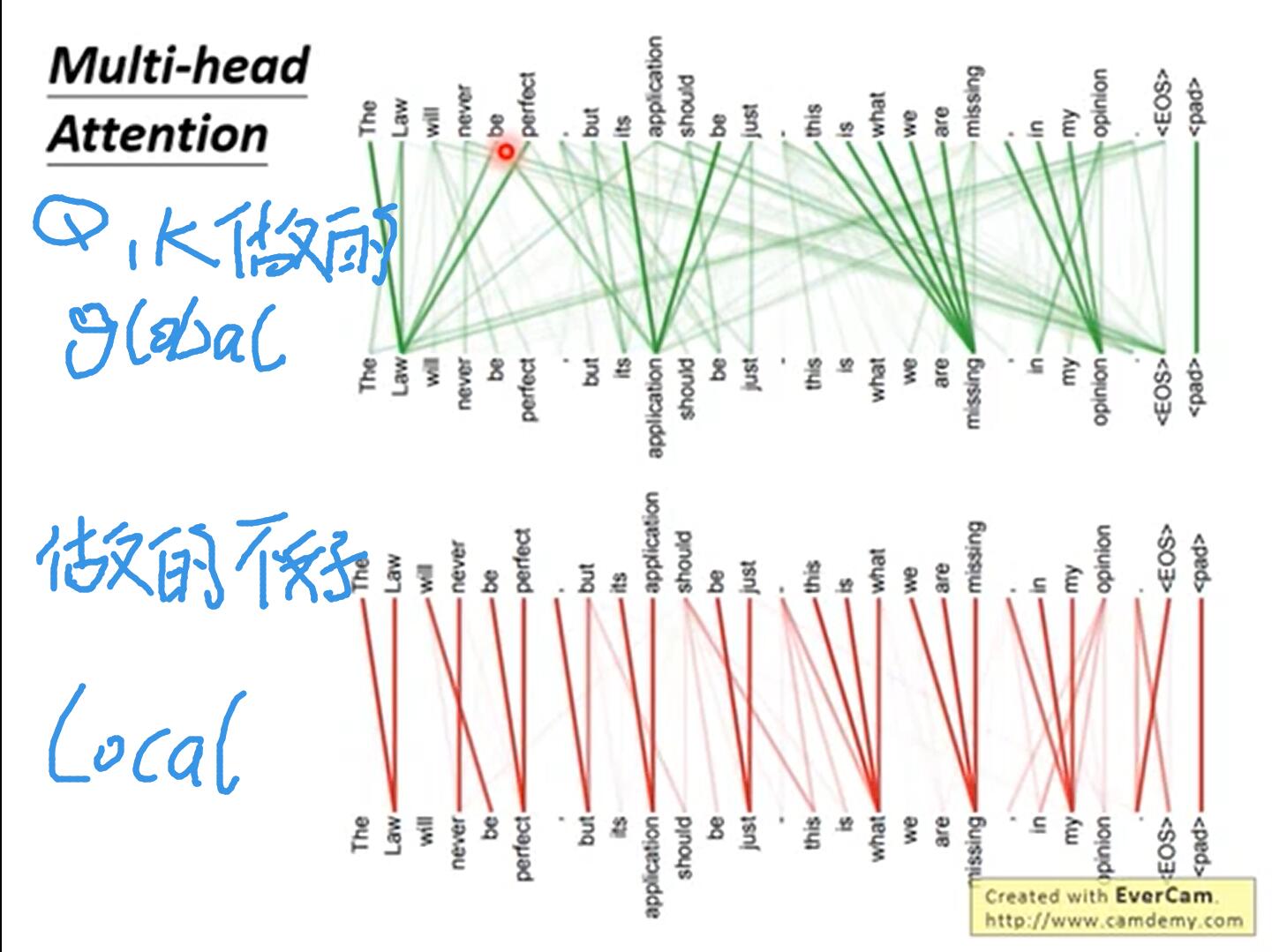
Firstly, 1x1 convolution reduces the channel dimension of higher-order characteristic graph f from C to a smaller dimension D. Since the transformer requires a sequence to be input, each channel of this feature is pulled into a vector to become the size of d X WH. Because this transformer has permutation invariance (the order of input has no effect on the result, so there is no location information directly), it needs to supplement the fixed location code as the input. Each encoder layer is composed of multi head self attention module and FFN. Each input will output a d-dimensional feature vector through the encoder.
Under the "multi head" attention mechanism, we maintain an independent query / key / value weight matrix for each head. We only need eight different weight matrix operations, and we will get eight different Z matrices
The left and right side of the encoder is only to serve the decoder. The input features are self attention weighted mapped. If there is a better backbone network, it can not be encoded at all
The input of encoder is: src, mask, pos_embed
class TransformerEncoder(nn.Module):
def __init__(self, encoder_layer, num_layers, norm=None):
super().__init__()
self.layers = _get_clones(encoder_layer, num_layers)#For encoder_layer copy num_layers times
self.num_layers = num_layers
self.norm = norm
def forward(self, src,
mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
output = src
for layer in self.layers:
output = layer(output, src_mask=mask,
src_key_padding_mask=src_key_padding_mask, pos=pos)
#output is encoded six times
if self.norm is not None:
output = self.norm(output)
return output
class TransformerEncoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):#Location coding
return tensor if pos is None else tensor + pos
#The difference between pre and post is whether there is normalization
def forward_post(self,
src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
q = k = self.with_pos_embed(src, pos)#Location code, pos + src
src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
src = src + self.dropout1(src2)# Addition similar to residual network
src = self.norm1(src)#layernorm, not batchnorm
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))#Two FFNS
src = src + self.dropout2(src2)
src = self.norm2(src)
return src
def forward_pre(self, src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
src2 = self.norm1(src)
q = k = self.with_pos_embed(src2, pos)
src2 = self.self_attn(q, k, value=src2, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
src = src + self.dropout1(src2)
src2 = self.norm2(src)
src2 = self.linear2(self.dropout(self.activation(self.linear1(src2))))
src = src + self.dropout2(src2)
return src
def forward(self, src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
if self.normalize_before:
return self.forward_pre(src, src_mask, src_key_padding_mask, pos)
return self.forward_post(src, src_mask, src_key_padding_mask, pos)
The output of the first five times is src for the next training. The output of the last time in the group is memory. Yo, about passing to the decoder, the two are the same, but the names are different
2.2.2Transformer decoder
Similar to the coding principle, it is to add the attention of coding decoding. Decoding is the key of Transformer. The front pile can be regarded as feature extraction. Decoding is to output the predicted category and regression coordinates.
His input is n object queries. After the self attention mechanism, it is mixed with the decoded output to encode and decode self attention. Then, through the feedforward network, they are independently decoded into frame coordinates and class labels, so as to generate N final predictions. Using self attention and encoding decoding attention to these embedded concerns, the model globally uses the pairwise relationship between all objects, and can use the whole image as context information
Input: memory: This is the output of the encoder. Size = [56,2256]
Mask: it's still the mask above
pos_embed: or the POS above_ embed
query_embed: randomly generated audience attention, size = [100,2256]
tgt: the input of the decoder of each layer. The first layer is equal to 0
class TransformerDecoder(nn.Module):
def __init__(self, decoder_layer, num_layers, norm=None, return_intermediate=False):
super().__init__()
self.layers = _get_clones(decoder_layer, num_layers)
self.num_layers = num_layers
self.norm = norm
self.return_intermediate = return_intermediate
def forward(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
output = tgt
intermediate = []
for layer in self.layers:
output = layer(output, memory, tgt_mask=tgt_mask,
memory_mask=memory_mask,
tgt_key_padding_mask=tgt_key_padding_mask,
memory_key_padding_mask=memory_key_padding_mask,
pos=pos, query_pos=query_pos)
if self.return_intermediate:
intermediate.append(self.norm(output))
if self.norm is not None:
output = self.norm(output)
if self.return_intermediate:
intermediate.pop()
intermediate.append(output)
if self.return_intermediate:
return torch.stack(intermediate)
return output.unsqueeze(0)
class TransformerDecoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)#Self attention
self.multihead_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)#And the above is the same thing, but it's decoding attention
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)#Feedforward neural network
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm3 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.dropout3 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):
return tensor if pos is None else tensor + pos
def forward_post(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
q = k = self.with_pos_embed(tgt, query_pos)
tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
return tgt
def forward_pre(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
tgt2 = self.norm1(tgt)
q = k = self.with_pos_embed(tgt2, query_pos)
tgt2 = self.self_attn(q, k, value=tgt2, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
tgt = tgt + self.dropout1(tgt2)
tgt2 = self.norm2(tgt)
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt2, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
tgt = tgt + self.dropout2(tgt2)
tgt2 = self.norm3(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt2))))
tgt = tgt + self.dropout3(tgt2)
return tgt
def forward(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
if self.normalize_before:
return self.forward_pre(tgt, memory, tgt_mask, memory_mask,
tgt_key_padding_mask, memory_key_padding_mask, pos, query_pos)
return self.forward_post(tgt, memory, tgt_mask, memory_mask,
tgt_key_padding_mask, memory_key_padding_mask, pos, query_pos)
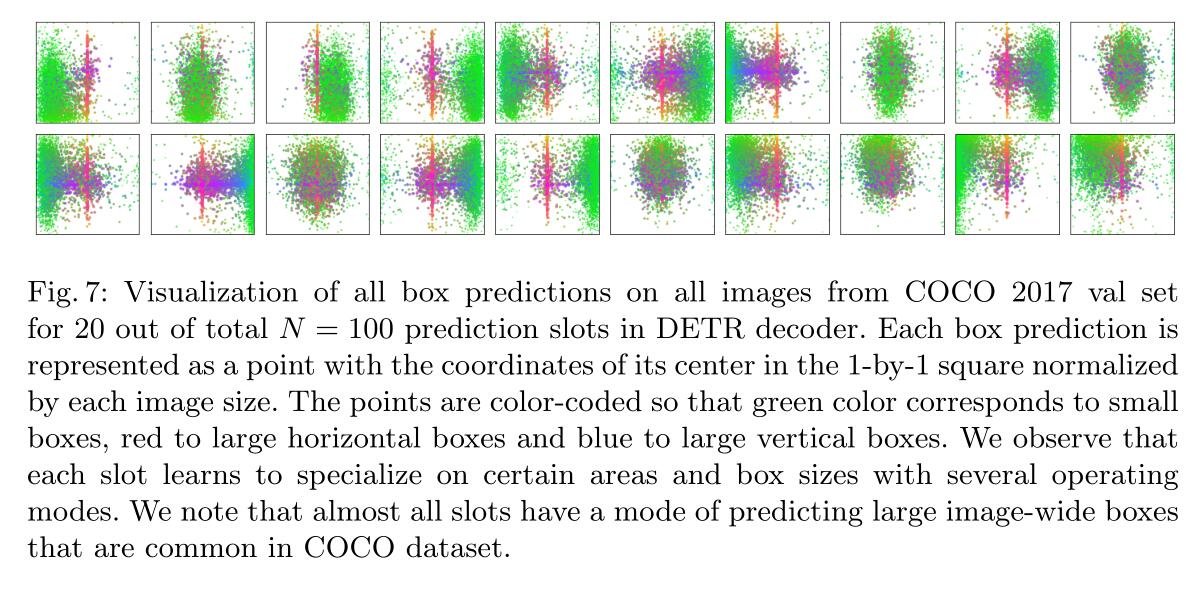
2.3Object querise
Is a set of random vectors generated to simulate the audience's attention. In the paper, n=100 audience's attention points are simulated. These attention points can have no target and are empty sets. And every audience will be inspired by the three colors – green color responses to small
boxes, red to large horizontal boxes and blue to large vertical boxes
There is a sentence in class detr:
self.query_embed = nn.Embedding(num_queries, hidden_dim)
This sentence is used to generate audience attention
num_embeddings (python:int) – the size of the dictionary. For example, if there are 5000 words in total, enter 5000. At this time, the index is (0-4999)
embedding_dim (python:int) – the dimension of the embedded vector, that is, how many dimensions are used to represent a symbol.
padding_idx (python:int, optional) – fill in the id, for example, the input length is 100, but the sentence length is different every time. Later, it needs to be filled with a unified number, and this number is specified here. In this way, when the network encounters the filled id, its correlation with other symbols will not be calculated. (initialized to 0)
max_norm (python:float, optional) – the maximum norm. If the norm of the embedded vector exceeds this limit, it must be re normalized.
norm_type (python:float, optional) – specifies what norm is used to calculate and is used to compare max_norm, the default is 2 norm.
scale_grad_by_freq (boolean, optional) – scale the gradient according to the frequency of words in mini batch. The default is False
sparse (bool, optional) – if True, the gradient associated with the weight matrix is transformed into a sparse tensor
First conduct the self attention of these Object querise, then use them to combine with the self attention generated by the encoder, and then do the encoding decoding attention. At this time, the feature is to add the feature of audience attention, and then do the FFN network to output the integrated information of class and bbox, and then send it to the two FFNS for classification and regression respectively
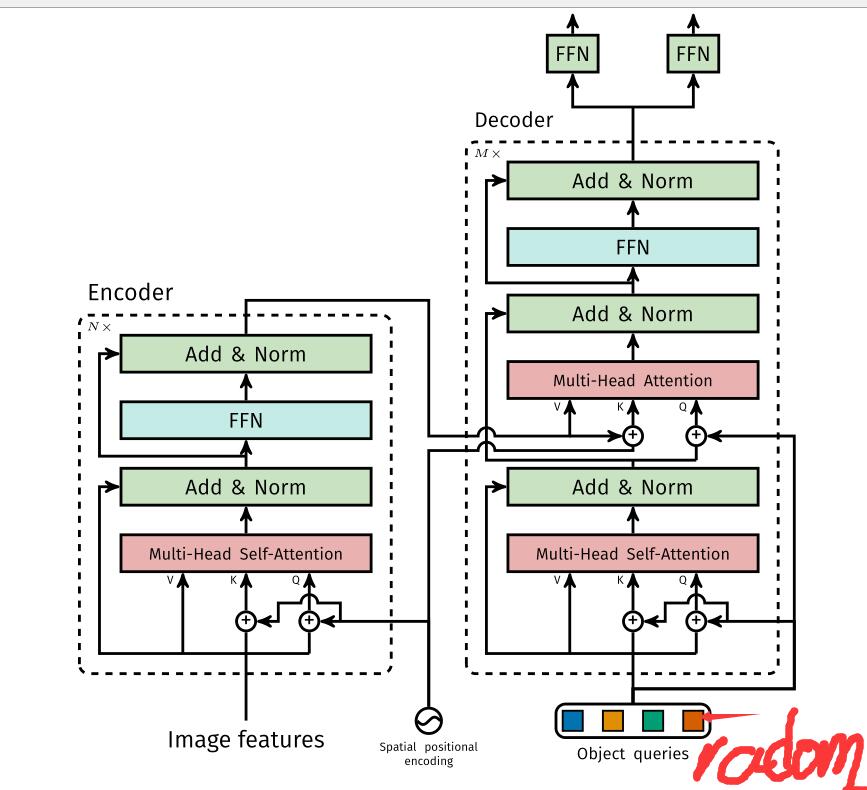
2.4 regression
class detr: define bbox_ Embedded and class_ Because the last class is FFN + BBS
self.bbox_embed = MLP(hidden_dim, hidden_dim, 4, 3)
self.class_embed = nn.Linear(hidden_dim, num_classes + 1)
FFN module, relatively simple
class MLP(nn.Module):
""" Very simple multi-layer perceptron (also called FFN)"""
def __init__(self, input_dim, hidden_dim, output_dim, num_layers):
super().__init__()
self.num_layers = num_layers
h = [hidden_dim] * (num_layers - 1)
self.layers = nn.ModuleList(nn.Linear(n, k) for n, k in zip([input_dim] + h, h + [output_dim]))
def forward(self, x):
for i, layer in enumerate(self.layers):
x = F.relu(layer(x)) if i < self.num_layers - 1 else layer(x)
return x
class detr:
outputs_class = self.class_embed(hs)
outputs_coord = self.bbox_embed(hs).sigmoid()
pred_logits:[2,100,classes+1]
outputs_coord:[2,100,4]
3. Loss function
Due to the special structure of DETR, the loss function should be reconstructed. The predicted number of images in den is usually more than the actual number of output images in 100. The main difficulty of prediction is to give a score to the output target (including category, location and size).
Y represents the set of N predictions. Since n is much larger than the number of targets in the figure, y should be used as ∅ pad. In order to find one with the least loss for N Y and N Y, it becomes the maximum matching problem of a bipartite graph, so the weighted Hungarian algorithm (km algorithm) can be used: recursively find a set of pairwise matching order with the least loss, and the key is to find the augmenting path – assuming that there is a matching result and there is a set of unmatched fixed points, The ability to find a path on which matching and unmatched fixed points appear alternately is called augmented path.
ps: the approximate optimal solution can also be obtained by greedy algorithm, and the amount of calculation is relatively small
In this way, the iou of gt and region proposal are calculated, and the non maximum suppression is no longer used to reduce the generation of region proposal, and the labor cost is reduced. The meaning of the following formula: find the pair with the smallest loss in the matching of Y and y, and finally find the minimum loss of all global pairs
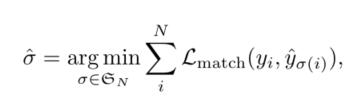
The loss function is a linear combination of category loss and box loss, with class loss on the left and box loss on the right.
Let's start with the loss: σ Pull out is in the case of optimal matching, p σ Is the probability at this time, and then take it as the index and take 10 as the base to calculate the cross entropy loss of logarithm (c is the real probability and p is the prediction probability). Since the category c in a picture must be less than n (n=100), c may be an empty set. When c is an empty set, reduce the log probability weight by 10 times to solve the imbalance between positive and negative samples.
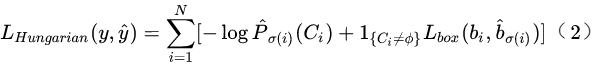
def loss_labels(self, outputs, targets, indices, num_boxes, log=True):
"""Classification loss (NLL)
targets dicts must contain the key "labels" containing a tensor of dim [nb_target_boxes]
"""
assert 'pred_logits' in outputs
src_logits = outputs['pred_logits']
idx = self._get_src_permutation_idx(indices)
target_classes_o = torch.cat([t["labels"][J] for t, (_, J) in zip(targets, indices)])
target_classes = torch.full(src_logits.shape[:2], self.num_classes,
dtype=torch.int64, device=src_logits.device)
target_classes[idx] = target_classes_o
loss_ce = F.cross_entropy(src_logits.transpose(1, 2), target_classes, self.empty_weight)#Cross entropy
losses = {'loss_ce': loss_ce}
The later bbox specific loss is the combination of L1 loss and IOU loss. If L1loss is used directly, loss is very sensitive to the size of the target, and the weight blue is not large. It is a super parameter, which should be set manually
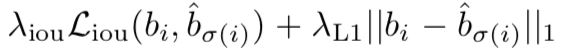
def loss_boxes(self, outputs, targets, indices, num_boxes):
"""Compute the losses related to the bounding boxes, the L1 regression loss and the GIoU loss
targets dicts must contain the key "boxes" containing a tensor of dim [nb_target_boxes, 4]
The target boxes are expected in format (center_x, center_y, w, h), normalized by the image size.
"""
assert 'pred_boxes' in outputs#An assertion is an if that will report an error
idx = self._get_src_permutation_idx(indices)
src_boxes = outputs['pred_boxes'][idx]
target_boxes = torch.cat([t['boxes'][i] for t, (_, i) in zip(targets, indices)], dim=0)
loss_bbox = F.l1_loss(src_boxes, target_boxes, reduction='none')
losses = {}#losses is a dictionary type
losses['loss_bbox'] = loss_bbox.sum() / num_boxes#Part I loss L1
loss_giou = 1 - torch.diag(box_ops.generalized_box_iou(
box_ops.box_cxcywh_to_xyxy(src_boxes),
box_ops.box_cxcywh_to_xyxy(target_boxes)))
losses['loss_giou'] = loss_giou.sum() / num_boxes#Part II loss
return losses
4. Experimental results