The so-called Brute force is to list all possible situations, and then check them one by one to find the answer. This method is simple, direct, does not play tricks, and makes use of the powerful computing power of the computer.
Violence laws are often synonymous with "inefficiency". However, compared with other "efficient" algorithms, the violence method is not only simple, but also has shorter coding and better writing. So when you get a problem, first think about how to solve it with violence. If the code of violence law can meet the time and space constraints required by the topic, use violence law. If the violence method can not meet the requirements, it can also be used as a comparison to verify the correctness of the advanced algorithm.
Depth first search (DFS) and width first search (BFS) are basic techniques, which are often used to solve the traversal problems of graphs and trees.
The roads in the maze are complicated. How can the mouse find the exit after entering from the entrance? There are two options:
- A mouse walks in a maze. At each intersection, it chooses to go to the right first (of course, it can also choose to go to the left first), and it can go as far as it can go; Until you hit a wall and can't go any further, then step back, take the left this time, and then continue to go down. In this way, as long as you don't encounter an exit, you will go all the way and won't repeat (it's stipulated here that going back doesn't count as repeating). This idea is DFS.
- A group of mice went through the maze. Assuming that there are an infinite number of mice, this group of mice will send some mice at each intersection to explore all the roads they haven't walked. If a mouse walking along a certain road can't move forward against a wall, it will stop; If other mice have explored the intersection, stop. Obviously, all roads will be reached before the exit, and will not be repeated. This idea is BFS.
In specific programming, BFS is generally realized with the data structure of queue, that is, "BFS = queue"; DFS is generally implemented by recursion, that is, "DFS = recursion".
Recursion is the process of deep search. You call yourself to gradually narrow down your big problem and replace it with a small problem.
The following is the calculation code of Fibonacci sequence:
#include<bits/stdc++.h>
using namespace std;
int cnt=0; //Counts how many recursions are performed
int fib (int n){ //Recursive function
cnt ++;
if (n == 1 || n == 2) //Reach the end, the last small problem
return 1;
return fib (n -1) + fib (n -2); //Call yourself twice, complexity O(2n)
}
int main(){
cout << fib(20); //Calculate the 20th Fibonacci number
cout <<" cnt="<<cnt; //Recursive cnt=13529 times
}Repeated calculations many times... To avoid repeated calculation of subproblems during recursion, you can save the result when the subproblem is solved. When you need the result again, you can directly return the saved result. This technique for storing the results of solved subproblems is called "Memoization". Memorization is a common optimization technique for recursion. The following is Fibonacci rewritten with "memorization + recursion":
#include<bits/stdc++.h>
using namespace std;
int cnt=0; //Counts how many recursions are performed
int data[25]; //Store Fibonacci number
int fib (int n){
cnt++;
if (n == 1 || n == 2) {
data[n]=1;
return data[n];
}
if(data[n]!=0) //Memory search: it has been calculated, so you don't have to calculate any more
return data[n];
data[n] = fib (n -1) + fib (n -2);
return data[n];
}
int main(){
cout << fib(20); //Calculate the 20th Fibonacci number
cout <<" cnt="<<cnt; //Recursive cnt=37 times.
}Self write full permutation (unordered)
#include<bits/stdc++.h>
using namespace std;
int a[20]={1,2,3,4,5,6,7,8,9,10,11,12,13};
void dfs(int s, int t){ //Full arrangement from the s-th number to the t-th number
if(s == t) { // Recursion ends, producing a full permutation
for(int i = 0; i <= t; ++i) //Output a spread
cout << a[i] << " ";
cout<<endl;
return;
}
for(int i = s; i <= t; i++) {
swap(a[s], a[i]); //Exchange the current first number with all subsequent numbers
dfs(s+1, t);
swap(a[s], a[i]); //Restore for next swap
}
}
int main(){
int n=3;
dfs(0, n-1); //Full arrangement of the first n numbers
}
Output results:
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
3 1 2Self writing full arrangement (sequence)
#include<bits/stdc++.h>
using namespace std;
int a[20]={1,2,3,4,5,6,7,8,9,10,11,12,13};
bool vis[20]; //Record whether the i-th number has been used
int b[20]; //Generate a full permutation
void dfs(int s,int t){
if(s == t) { //Recursion ends, producing a full permutation
for(int i = 0; i < t; ++i) //Output a spread
cout << b[i] << " ";
cout<<endl;
return;
}
for(int i=0;i<t;i++)
if(!vis[i]){
vis[i]=true;
b[s]=a[i];
dfs(s+1,t);
vis[i]=false;
}
}
int main(){
int n=3;
dfs(0,n); //Full arrangement of the first n numbers
return 0;
}
Output is:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1What if you want to print the arrangement of any # m # number in # n # number?
If you want to take the arrangement of any # 3 # numbers in # 4 # numbers, only change the # 2 # line to # n=4, and then modify the # 7 # line in # dfs():
if(s == 3) { //Recursion ends, producing a permutation
for(int i = 0; i < 3; ++i) //Output a spread
cout << b[i] << " ";
cout<<endl;
return;
}
result:
1 2 3
1 2 4
1 3 2
1 3 4
1 4 2
1 4 3
2 1 3
2 1 4
2 3 1
2 3 4
2 4 1
2 4 3
3 1 2
3 1 4
3 2 1
3 2 4
3 4 1
3 4 2
4 1 2
4 1 3
4 2 1
4 2 3
4 3 1
4 3 2
Maze - Blue Bridge cloud course (lanqiao.cn)
Fortunately, the answer is very simple.
#include<bits/stdc++.h>
using namespace std;
const int n=10;
char mp[n+2][n+2]; //Store maze with matrix mp[][]. Define static arrays globally
bool vis[n+2][n+2]; //Whether the judgment point has passed is the "memory" function
int ans = 0;
int cnt = 0;
bool dfs(int i, int j){
if (i<0 || i>n-1 || j<0 || j>n-1) return true; //Out of the maze, stop
if (vis[i][j]) return false; //If it has been searched, it means that you have gone in circles and can't go out
cnt++; //How many times has dfs() been counted
vis[i][j] = true; //Tag searched
if (mp[i][j] == 'L') return dfs(i, j - 1); //Left, continue dfs
if (mp[i][j] == 'R') return dfs(i, j + 1); //To the right
if (mp[i][j] == 'U') return dfs(i - 1, j); //Up
if (mp[i][j] == 'D') return dfs(i + 1, j); //down
return true;//You have to add it, or warning
}
int main(){
//This question is to fill in the blank and output the answer directly:
// cout << 31; return 0;
//If you don't fill in the blanks, write the following code:
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> mp[i][j]; //Read maze
for (int i = 0; i < n; i++) //For each point, judge whether it can go out
for (int j = 0; j < n; j++){
memset(vis, 0, sizeof(vis)); //Clear vis [] before searching each point
if(dfs(i, j)) ans++; //Click mp[i][j] to go out and count the answers
}
cout <<"ans="<< ans <<", cnt="<<cnt<< endl; //Output answer
return 0;
}Complexity analysis: if the maze has ＾ n rows and ＾ n columns, do ＾ dfs(), then you need to go through all points at most, that is, ＾ O(n^2) times. Lines 25-29 of the code do a dfs() for n^2 points, so the total complexity is O(n^4).
If n is 10, it will not time out, but if n is 1000, the code will time out severely.
DFS is a violent technology that searches for all possible situations.
Algorithm optimization: let's consider optimizing the previous code of {O(n^4). By observing, you will find that you don't have to do a DF () for each point. For example, if you start from a point, walk a path, and finally walk out of the maze, you can walk out of the maze with all the points on the path as the starting point; If the path goes round and round, all points on the path cannot get out of the maze. Therefore, if we have a way to record the path, we can greatly reduce the amount of calculation. Therefore, the key to optimization is how to mark the whole path.
#include<bits/stdc++.h>
using namespace std;
const int n=10;
char mp[n+2][n+2];
bool vis[n+2][n+2];
int solve[n+2][n+2]; //solve[i][j]=1 means that this point can go out= 2 show no go
int ans = 0;
int cnt = 0;
bool dfs(int i, int j){
if (i<0 || i>n-1 || j<0 || j>n-1) return true;
if(solve[i][j]==1) return true; //Point (i,j) has been calculated. Can you go out
if(solve[i][j]==2) return false; //Point (i,j) has been calculated and can't get out
if (vis[i][j]) return false;
cnt++; //How many times has dfs() been counted
vis[i][j] = true;
if (mp[i][j] == 'L'){
if(dfs(i, j - 1)){ solve[i][j] = 1;return true;}
//Go back and record that the whole path can go out
else { solve[i][j] = 2;return false;}
//Go back and record that the whole path can't get out
}
if (mp[i][j] == 'R') {
if(dfs(i, j + 1)){ solve[i][j] = 1;return true;}
else { solve[i][j] = 2;return false;}
}
if (mp[i][j] == 'U') {
if(dfs(i - 1, j)){ solve[i][j] = 1;return true;}
else { solve[i][j] = 2;return false;}
}
if (mp[i][j] == 'D') {
if(dfs(i + 1, j)){ solve[i][j] = 1;return true;}
else { solve[i][j] = 2;return false;}
}
}
int main(){
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> mp[i][j];
memset(solve, 0, sizeof(solve));
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++){
memset(vis, 0, sizeof(vis));
if(dfs(i, j)) ans++;
}
cout <<"ans="<< ans <<",cnt="<<cnt<< endl;
return 0;
} The above is the optimized code. In the code, I marked the whole path > with {solve [] []:
- When △ solve[i][j]=1, it means that the point (i, j) can go out;
- When ， solve[i][j]=2, it indicates that it cannot go.
Let's take the behavior of {17-20 as an example: when the return value of} dfs(i, j - 1) is} true, indicating that (i, j-1) can go out, then its previous point (i, j) can go out naturally. At this time, record solve[i][j]=1. If the return value of △ dfs(i, j - 1) is △ false, it means that (i, j-1) cannot go out, and its previous point (i, j) cannot go out. Record △ solve[i][j]=2. In the process of returning to the starting point step by step, the result of {solve [] [] of points on the whole path is obtained.
Complexity analysis: the total complexity is O(n^2) because the answer can be obtained only by assigning a value to {solve [] [] of each point in the maze. Because the maze problem has a total of n^2 points, and each point needs to be found, O(n^2) is the best complexity that can be achieved. At the same time, the code also counts the number of times of {dfs() with {cnt} and outputs: cnt=100, indicating that it is searched just once at each point.
Grid segmentation - Blue Bridge cloud course (lanqiao.cn)
That's a good question,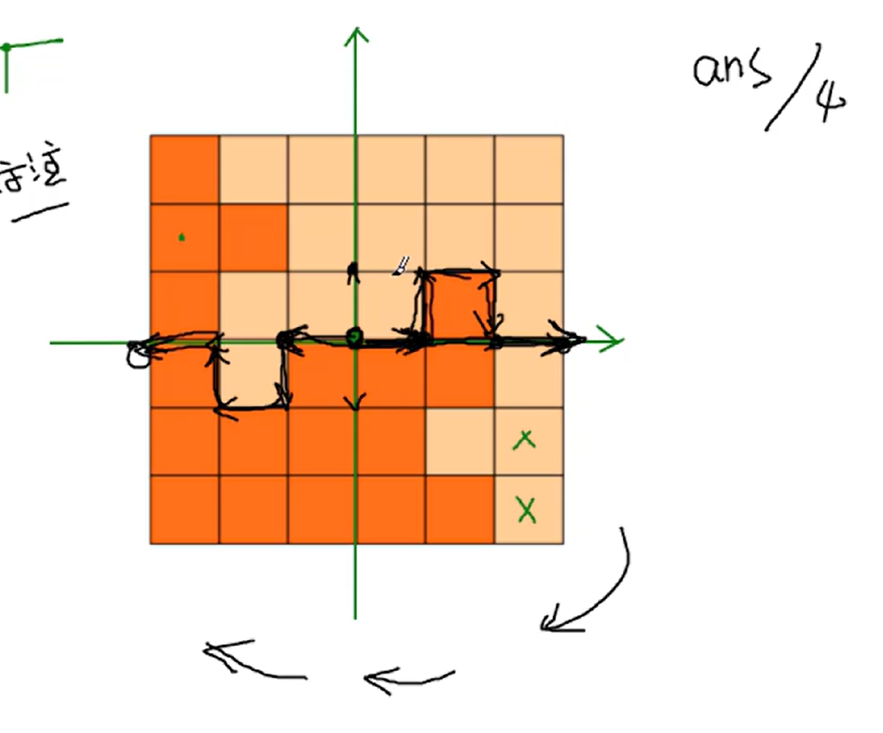
First, the cutting line must pass through the center point of the graph. As long as half of the dividing line reaching the boundary is determined, the other half can be drawn symmetrically according to this half. In addition, the topic requires that rotational symmetry belongs to the same segmentation method, because the result is centrosymmetric, and the number of searches can be divided by ＾ 4 ＾. However, in the search process, it should be noted that half of the searched split line cannot pass through two points about central symmetry at the same time, so the symmetrical points need to be marked when marking.
dfs from the middle point
#include<bits/stdc++.h>
using namespace std;
int X[] = {0, -1, 1, 0, 0}; //Up, down, left and right
int Y[] = {0, 0, 0, -1, 1};
bool vis[10][10]; //Mark whether the point has been accessed
int res = 0;
void dfs(int x, int y){
if(x == 0 || y == 0 || x == 6 || y == 6){
res++;
return ;
}
for(int i = 1 ; i <= 4 ; i++){ //Up, down, left and right
x += X[i]; y += Y[i]; //Take a step
if(!vis[x][y]){ // If the point is not accessed, continue to search deeply
vis[x][y] = true; // The current point is labeled as accessed
vis[6 - x][6 - y] = true;
dfs(x, y); // Keep searching
vis[6 - x][6 - y] = false;
vis[x][y] = false;
}
x -= X[i]; y -= Y[i];
}
}
int main(){
vis[3][3] = true;
dfs(3, 3);
cout << res / 4 << endl;
return 0;
}Regularization problem - Blue Bridge cloud course (lanqiao.cn)
This code is also very good, with distinct layers.
Our ideas and steps are as follows:
- A left parenthesis must match a right parenthesis: you can try to generate all kinds of nested parentheses by starting with the first pair of parentheses "()"; Insert the left bracket and the right bracket of the (2nd) pair of brackets into any position of the (1st) pair of brackets at random, such as "(())"; Then insert the (3rd) pair of brackets randomly, such as "(() ()", and so on. As long as the parentheses are inserted in pairs, the resulting parenthesis string is legal.
- Check the validity of parentheses with the stack: each time you encounter an open parenthesis' (', you enter the stack, and each time you encounter a right parenthesis')', you complete a match and exit the stack. If you are not familiar with it, you can practice with a nested bracket.
- Coding: you can directly use stack coding or DFS (recursive) coding, which is simpler.
#include<bits/stdc++.h>
using namespace std;
string s;
int pos = 0; //Current location
int dfs(){
int tmp = 0, ans = 0;
int len = s.size();
while(pos < len){
if(s[pos] == '('){ //Left parenthesis, continue recursion. Equivalent to stacking
pos++;
tmp += dfs();
}else if(s[pos] == ')'){ //Right parenthesis, recursive return. Equal to out of stack
pos++;
break;
}else if(s[pos] == '|'){ //Check or
pos++;
ans = max(ans, tmp);
tmp = 0;
}else{ //Check X and count the number of X
pos++;
tmp++;
}
}
ans = max(ans, tmp);
return ans;
}
int main(){
cin >> s;
cout << dfs() << endl;
return 0;
}Winter vacation assignment - Blue Bridge cloud class (lanqiao.cn)
Mengxin (timeout) code:
#include <bits/stdc++.h>
using namespace std;
int a[20] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13};
int main() {
int ans=0;
do{
if( a[0]+a[1]==a[2] && a[3]-a[4]==a[5]
&&a[6]*a[7]==a[8] && a[11]*a[10]==a[9])
ans++;
}while(next_permutation(a,a+13));
cout<<ans<<endl;
}Because 13= 6227020800. However, the analysis of the topic shows that it is not necessary to generate a complete arrangement. For example, if the first 3 numbers of an arrangement do not meet "□ + □ = □", the next 9 numbers are wrong no matter how they are arranged. This technology of early termination of search is called pruning. Pruning is a common optimization technology in search. Because {next_permutation() must generate a complete permutation every time, and cannot stop in the middle, so it is not easy to use in this situation.
Therefore, we can use the arrangement code introduced at the beginning, either in order or not.
//First arrangement code
#include <bits/stdc++.h>
using namespace std;
int a[20] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13};
int ans = 0;
void dfs(int s, int t)
{
if (s == 12) {
if(a[9] * a[10] == a[11]) ans++;
return;
}
//The first three numbers cannot meet the conditions
if (s == 3 && a[0] + a[1] != a[2]) return;
//The first 6 numbers cannot meet the conditions
if (s == 6 && a[3] - a[4] != a[5]) return;
//The first 9 numbers cannot meet the conditions
if (s == 9 && a[6] * a[7] != a[8]) return;
for (int i = s; i <= t; i++) {
swap(a[s], a[i]);
dfs(s+1, t);
swap(a[s], a[i]);
}
}
int main()
{
int n = 13;
dfs(0, n - 1);
cout << ans;
return 0;
}//The second arrangement code, order
#include<bits/stdc++.h>
using namespace std;
int a[20]={1,2,3,4,5,6,7,8,9,10,11,12,13};
bool vis[20];
int b[20];
int ans=0;
void dfs(int s,int t){
if(s==12) {
if(b[9]*b[10] == b[11]) ans++;
return;
}
if(s==3 && b[0]+b[1]!=b[2]) return; //prune
if(s==6 && b[3]-b[4]!=b[5]) return; //prune
if(s==9 && b[6]*b[7]!=b[8]) return; //prune
for(int i=0;i<t;i++)
if(!vis[i]){
vis[i]=true;
b[s]=a[i];
dfs(s+1,t);
vis[i]=false;
}
}
int main(){
int n=13;
dfs(0,n); //Full arrangement of the first n numbers
cout<<ans;
return 0;
}
OK, that's the end of the example. Let's give a DFS framework and have a good experience.
ans; //The answer is expressed in global variables
void dfs(Number of layers, other parameters){
if (Exit judgment){ //Reach the lowest level, or exit if conditions are met
Update answer; //The answer is generally expressed in global variables
return; //Return to the previous level
}
(prune) //Prune before further DFS
for (Enumerate the possible situations of the next layer) //Continue DFS for each case
if (used[i] == 0) { //If state i is not used, you can enter the next layer
used[i] = 1; //Mark the status i, indicating that it has been used and can no longer be used at the lower level
dfs(Number of layers+1，Other parameters); //Next floor
used[i] = 0; //Restoring the state does not affect the use of this state by the previous layer during backtracking
}
return; //Return to the previous level
}