Prefix sum is an important preprocessing tool in the algorithm.

Okay, I can't make it up anymore, it seems I don't have any [doge]

Differential operations, which can be said to be the inverse of the sum of prefixes, are often used together with the prefix to solve some interval problems.

Recently, I also encountered a lot of difference problems, so I am ready to summarize one article. Here, we will focus on the prefixes and differences between one and two dimensions. Say nothing more.

Prefix and;

In one dimension, there's nothing to say.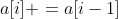

Let's look at two dimensions:

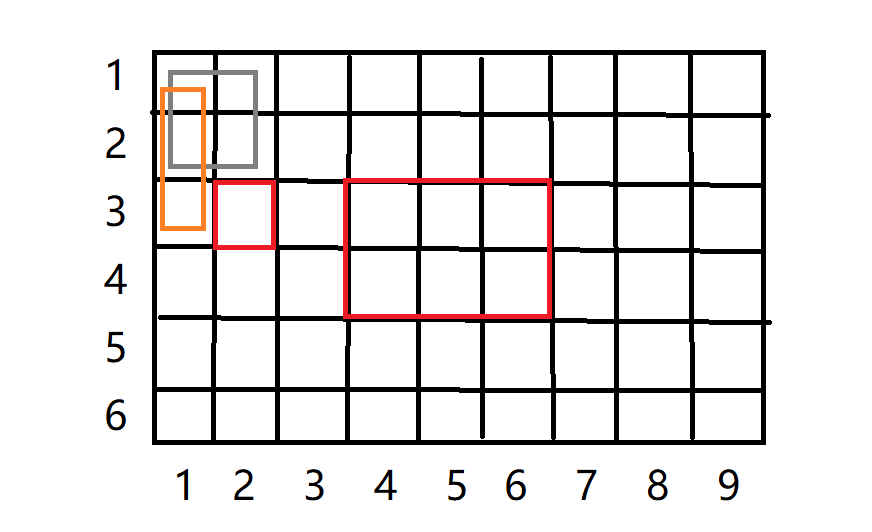
Let's first look at the prefix and requirements for a point [2,3]:

As you can see, if we want to, we'll add the sum of all the points from [1,1] to [2,3];

The point is how we add it;

When we calculate the sum of [2,3] prefixes, [2,2] and [1,3] must have been calculated;

So what we can see is that the prefix sums of [2,2] and [1,3] are contained within [2,3] and contain [1,2] repeatedly

So: (s: prefix and array, a: original array)

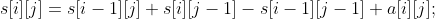
Okay, I'm sure you've learned it.

Let's see how prefixes and intervals are needed. (For example, let's calculate the interval prefix of the Red Square and [6,4], [4,3])

We find the same, so cut off the extra chops;

But we found that the extra part [3,2] was cut twice during the cutting process, so we have to add this part in the end.

So

;

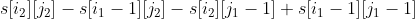Okay, then we can do the whole thing;

 Territory Selection - Lo Valley

You don't have to explain this [doge]

#include<bits/stdc++.h>
using namespace std;

const int N = 1010;
typedef long long LL; 
int n,m,c;

int a[N][N];

LL s[N][N];
int main()
{
	
	cin>>n>>m>>c;
	for(int i =1 ;i <= n;i ++)
		for(int j =1 ;j <=m ;j ++)
			cin>>a[i][j];
	
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			s[i][j] = s[i-1][j] + s[i][j-1]- s[i-1][j-1] + a[i][j];
	
	LL res = -1e8;
	int x,y;
	for(int i =1 ;i <= n -c + 1 ;i ++)
		for(int j = 1 ;j <= m -c + 1 ;j ++)
		{
			int x1,y1,x2,y2;
			x1= i;
			y1 = j;
			x2 = i + c -1;
			y2 = j + c -1;
			
			LL mx = s[x2][y2]- s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];
			if(mx > res)
			{
				res = mx;
				x = i,y = j;
			}
		}
	cout<<x<<" "<<y<<endl; 
	return 0;
}

Difference;

Reverse the process; a[i] -= a[i-1];

So if we want to get the original array, we just need a[i] += a[i-1] (prefix and);

As mentioned above, the most common use of difference is to maintain an interval so that each operation contributes the same amount to that interval.

The saying is: add a value to the number in this area;

Look directly at the picture;

How do we want to add 1 to [3,5]?

If we consider the values of prefix and, prefix and the first number in the middle, we will make a contribution to all subsequent numbers. Then we add 1 to 3, which will make a contribution to all subsequent numbers 1, but I just want to add 5, that is, we don't want to add the contribution to 6, so we can subtract 1 from 6. This contribution does not contribute to subsequent numbers from 6 onwards.

 

We do the same;

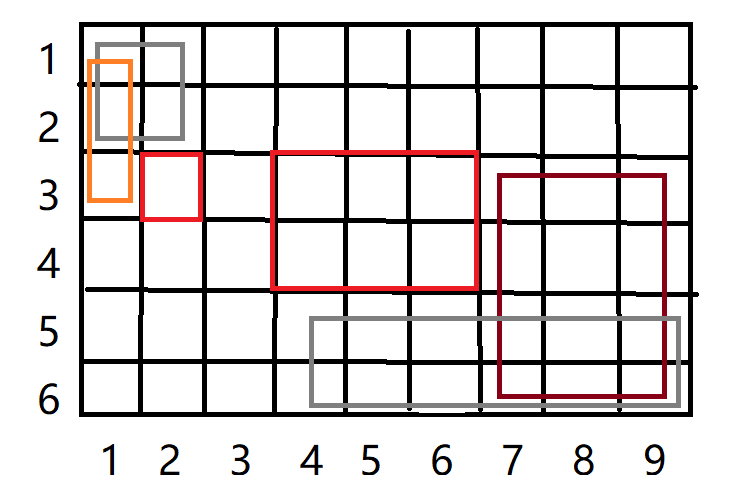
We want to add 1 to [4,3]-- [4,6];

Adding 1 to [4,3] will contribute to all points in the lower right corner of that point;

So we subtract contributions from other parts;

We add -1 to [4,5] so that the gray box is not contributed by [4,3] plus 1; The addition of -1 to [7,3] results in the dark red box not being contributed by [4,3] plus 1;

However, there is overlap, and we subtract a little more, so we add one on [7,5] to add the extra subtraction back;

Let's talk about the whole difference.

Submarine High-Speed Rail-Lough Valley

#include<bits/stdc++.h>
using namespace std;

const int N  = 100010;
typedef long long LL;


LL n,m;
queue<int> p;

LL a[N],b[N],c[N];

LL s[N];
LL res;
int main()
{
	scanf("%d%d",&n,&m);
	
	for(int i =1;i <= m;i ++)
	{
		int c;
		scanf("%d",&c);
		p.push(c);
	} 
	
	for(int i =1;i <= n - 1 ;i ++)	scanf("%d%d%d",&a[i],&b[i],&c[i]);
		
	int st,ed;
	st = p.front(),p.pop();
	while(!p.empty())
	{
		ed = p.front(), p.pop();
		
		if(st > ed)
		{
			s[ed] ++;
			s[st] --;	
		} 
		else 
		{
			s[st] ++;
			s[ed] --;
		}
		st = ed;
	}
	
	for(int i =1 ;i <= n - 1 ;i ++) s[i] += s[i - 1];
	
	
	for(int i =1 ;i <= n-1 ; i ++)
	{
		if(s[i] * a[i] > s[i]* b[i] + c[i]) res += s[i]* b[i] + c[i];
		else res += s[i] * a[i];
	}
	
	printf("%lld\n",res);
	return 0;
} 

Close your work;