preface

Review the content of the basic course of acwing algorithm. This article is to explain the basic algorithm: dynamic programming - digital statistics DP. About time complexity: bloggers are not very good at computing at present. They will make up for it in the future.

1, Dynamic programming

Dynamic Programming (DP) is the process of solving the optimization of the decision-making process. I personally think it is the most around of all the algorithms I have contacted at present

The solution to the problem here comes from: y total Yan's dp analysis

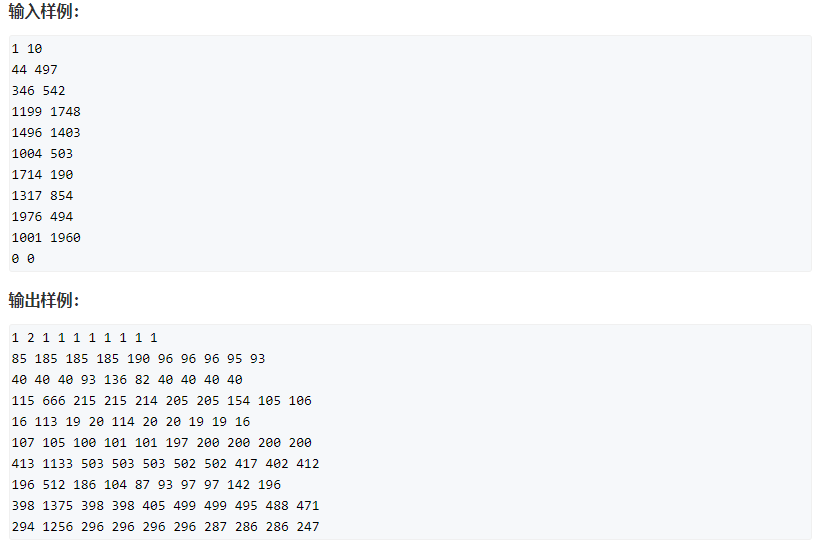
2, AcWing 338 Counting problem

Link to this question: AcWing 338. Counting problem
This blog provides screenshots of this topic:

Analysis of this problem

Describe the purpose of the function in the code:
int count(int n, int x): returns the number of times x occurs in 1 ~ n
Int get (vector < int > num, Int l, int r): returns the number of bits from R to L in the num array
int power10(int x): returns the x power of 10

Let's look at the analysis process:
How to find the number of occurrences of i in a ~ b: Using Prefix and count(b, i) - count(a - 1, i)

Here's how to implement the count function:
Suppose we need to find the number of occurrences of 1 in 1 ~ n, n = abcdefg
Our idea is: calculate the number of occurrences of 1 in each bit respectively. Here, we assume to calculate the number of occurrences of 1 in the fourth bit, that is, 1 < = xxx1yyy < = ABCDEFG
Analyze in two general directions:
(1) xxx = 000 ~ abc - 1: in this case, the value of yyy is: 000 ~ 999, so the total number of such cases is: abc * 1000
(2) xxx = abc:
(2.1) if d < 1, then abc1yyy > abc0efg, so there is no number in line with the situation
(2.2) d = 1, the value of yyy can be 000 ~ efg, so the total number of such cases is: efg + 1
(2.3) d > 1, yyy can be 000 ~ 999, so the total number of such cases is 1000

Here's the special judgment:
In the above example, we use 1 as an example. Next, let's consider the most special number: 0
0 will not affect part (2) of the above count function implementation, but only part (1): numbers such as 0123 cannot appear
In the above case, the value range of (1) xxx should be 001 ~ abc - 1, which can prevent the occurrence of leading 0. When we traverse the number of 0 on each bit in turn, because the first cannot be 0, the for loop can be written as: for (int i = n - 1 -! X; I > = 0; I --)

AC code

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 10;

int get(vector<int> num, int l, int r)
{
    int res = 0;
    for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
    return res;
}

int power10(int x)
{
    int res = 1;
    while (x -- ) res *= 10;
    return res;
}

int count(int n, int x)
{
    if (!n) return 0;

    vector<int> num;
    while (n)
    {
        num.push_back(n % 10);
        n /= 10;
    }
    n = num.size();

    int res = 0;
    for (int i = n - 1 - !x; i >= 0; i -- )
    {
        if (i < n - 1)
        {
            res += get(num, n - 1, i + 1) * power10(i);
            if (!x) res -= power10(i);       //Special judgment on 0, that is, the case of subtracting 001
        }

        if (num[i] == x) res += get(num, i - 1, 0) + 1;
        else if (num[i] > x) res += power10(i);
    }

    return res;
}

int main()
{
    int a, b;
    while (cin >> a >> b , a)
    {
        if (a > b) swap(a, b);    //The data in the title is relatively small, and a > B may occur, so it needs special judgment

        for (int i = 0; i <= 9; i ++ )
            cout << count(b, i) - count(a - 1, i) << ' ';
        cout << endl;
    }

    return 0;
}

3, Time complexity

For the time complexity and proof of dynamic programming - digital statistics DP, a detailed description and proof process will be given later. At present, I'll start.