int Max3( int A, int B, int C )
{ /* Returns the maximum of 3 integers */
    return A > B ? A > C ? A : C : B > C ? B : C;
}
 
int DivideAndConquer( int List[], int left, int right )
{ /* Divide and conquer to find the maximum sum of sub columns from List[left] to List[right] */
    int MaxLeftSum, MaxRightSum; /* Storing solutions of left and right subproblems */
    int MaxLeftBorderSum, MaxRightBorderSum; /*Store results across boundaries*/
 
    int LeftBorderSum, RightBorderSum;
    int center, i;
 
    if( left == right )  { /* The termination condition of recursion. The child column has only one number */
        if( List[left] > 0 )  return List[left];
        else return 0;
    }
 
    /* Here is the process of "dividing" */
    center = ( left + right ) / 2; /* Find the midpoint */
    /* Recursively finding the maximum sum of the two side sub columns */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );
 
    /* Find the sum of the largest subcolutions across the boundary line below */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* Scan from midline to left */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* End of left scan */
 
    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* Scan right from midline */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* End of right scan */
 
    /* Now return the result of "governance" */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
 
int MaxSubseqSum3( int List[], int N )
{ /* Keep the same function interface as the first two algorithms */
    return DivideAndConquer( List, 0, N-1 );
}

Application conditions of divide and conquer method:
1. The original problem can be divided into several solutions to the original problem;
2. The subproblem can be decomposed and solved;
3. The solution of the subproblem can be merged into the solution of the original problem;
4. The decomposed subproblems should be independent of each other, that is, they do not contain overlapping subproblems

 

MaxLeftSum, MaxRightSum; the maximum value of a single small block can be calculated (for example, 1, 2, -3,4, which can indicate that there is an independent maximum sub column 4 on the right)

MaxLeftBorderSum, MaxRightBorderSum; these two are responsible for finding the maximum value of the whole sequence

 

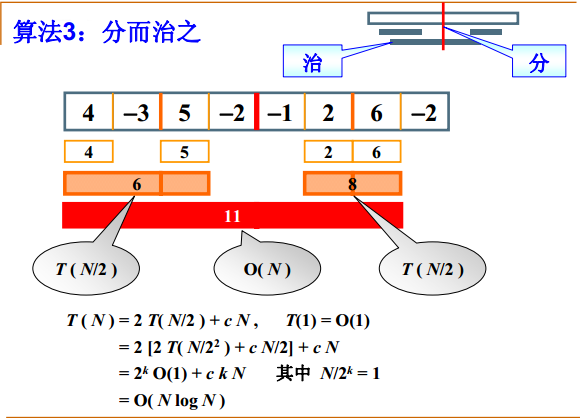
Let the total time complexity be T(N), divide it into two parts, each side is T(N/2), and add o (N) (it means that every element has been scanned once, i.e. the constant times of N), till N/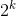=1, that is, the termination of recursion. The left and right sides are equal. T(1)=O(1)，k =logN,  =N,ckN=cNlogN=O(NlogN)

When the two complexities are together, we take the larger O(NlogN),