I. divide and conquer algorithm
1. How to understand divide and conquer algorithm
Divide and conquer algorithm is to divide the original problem into n sub problems with small scale and similar structure to the original problem, solve these sub problems recursively, and then combine the results to get the solution of the original problem.
In the recursive implementation of divide and conquer algorithm, each layer of recursion involves three operations as follows:
- Decomposition: decompose the original problem into a series of subproblems
- Solution: recursively solve each subproblem. If the subproblem is small enough, directly solve it.
- Merge: merge the results of sub problems into the original problems
The problems that divide and conquer algorithm can solve generally need to meet the following conditions:
- The original problem has the same pattern as the small problem
- The subproblem decomposed from the original problem can be solved independently, and there is no correlation between subproblems.
- There are decomposition termination conditions, that is, when the problem is small enough, it can be solved directly
- The subproblem can be merged into the original problem, and the complexity of the merging operation cannot be too high, otherwise it will not reduce the overall complexity of the algorithm.
2. Problems related to divide and conquer algorithm
1),LeetCode50: Pow(x, n)
To realize pow(x, n), that is, to calculate the N-power function of X
Example 1:
Input: 2.00000, 10 Output: 1024.00000
Example 2:
Input: 2.10000, 3 Output: 9.26100
Example 3:
Input: 2.00000, - 2 Output: 0.25000 Explanation: 2-2 = 1 / 22 = 1 / 4 = 0.25
Explain:
-100.0 < x < 100.0 n is a 32-bit signed integer with a value range of [− 231, 231 − 1]
Explanation:
public double myPow(double x, int n) { if (n < 0) { x = 1 / x; n = -n; } return helper(x, n); } private double helper(double x, int n) { if (n == 0) return 1.0; double half = helper(x, n / 2); if (n % 2 == 0) return half * half; else return half * half * x; }
2),LeetCode169: Seek mode
Given an array of size n, find the mode. Mode refers to an element that occurs more than n/2n/2n/2 times in an array
You can assume that an array is not empty and that there is always a mode for a given array
Example 1:
Input: [3,2,3] Output: 3
Example 2:
Input: [2,2,1,1,1,2,2] Output: 2
Explanation:
public int majorityElement(int[] nums) { return helper(0, nums.length - 1, nums); } private int helper(int low, int high, int[] nums) { if (low == high) return nums[low]; int mid = low + ((high - low) >> 1); int left = helper(low, mid, nums); int right = helper(mid + 1, high, nums); if (left == right) return left; int leftCount = countInRange(left, low, high, nums); int rightCount = countInRange(right, low, high, nums); return leftCount > rightCount ? left : right; } private int countInRange(int num, int low, int high, int[] nums) { int count = 0; for (int i = low; i <= high; ++i) { if (nums[i] == num) count++; } return count; }
2. Backtracking algorithm
1. How to understand backtracking algorithm
The processing idea of backtracking is similar to enumeration search. By enumerating all the solutions, we can find the solution that meets the expectation. In order to enumerate all possible solutions regularly and avoid omission and repetition, we divide the problem solving process into several stages. At each stage, we will face a fork in the road. First, we will choose a road at will. When we find that the road is impassable (not in line with the expected solution), we will go back to the previous fork in the road and choose another way to continue.
2. Related topics of backtracking algorithm
1),LeetCode22: bracket-generating
Given that n represents the logarithm of generating parentheses, please write a function that can generate all possible and valid combinations of parentheses.
For example, given n=3, the result is:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ]
Explanation:
public List<String> generateParenthesis(int n) { List<String> list = new ArrayList<>(); helper(0, 0, n, "", list); return list; } private void helper(int left, int right, int max, String currentStr, List<String> list) { if (left == max && right == max) { list.add(currentStr); return; } if (left < max) { helper(left + 1, right, max, currentStr + "(", list); } if (right < left) { helper(left, right + 1, max, currentStr + ")", list); } }
2),LeetCode78: subset
Given a set of integer array nums without repeating elements, all possible subsets (power sets) of the array are returned.
**Note: * * the solution set cannot contain duplicate subsets
Example:
Input: nums = [1,2,3] Output: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
Explanation:
List<List<Integer>> result = new ArrayList<>(); public List<List<Integer>> subsets(int[] nums) { if (nums.length == 0) return result; helper(0, nums, new ArrayList<>()); return result; } private void helper(int level, int[] nums, List<Integer> list) { if (level == nums.length) { result.add(new ArrayList<Integer>(list)); return; } helper(level + 1, nums, list); list.add(nums[level]); helper(level + 1, nums, list); list.remove(list.size() - 1); }
3),LeetCode17: Letter combination of telephone number
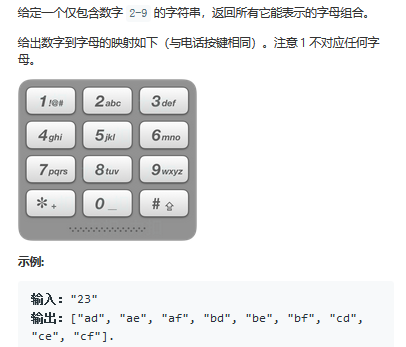
Explanation:
Map<Character, String> phone = new HashMap<Character, String>() {{ put('2', "abc"); put('3', "def"); put('4', "ghi"); put('5', "jkl"); put('6', "mno"); put('7', "pqrs"); put('8', "tuv"); put('9', "wxyz"); }}; List<String> result = new ArrayList<>(); public List<String> letterCombinations(String digits) { if (digits.length() == 0) return result; helper(0, digits, ""); return result; } private void helper(int level, String digits, String currentStr) { if (level == digits.length()) { result.add(currentStr); return; } String latters = phone.get(digits.charAt(level)); for (int i = 0; i < latters.length(); ++i) { helper(level + 1, digits, currentStr + latters.charAt(i)); } }
4),LeetCode46: Full Permutation
Given a sequence without repeating numbers, all possible permutations are returned
Example:
Input: [1,2,3] Output: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
Explanation:
List<List<Integer>> result = new ArrayList<>(); public List<List<Integer>> permute(int[] nums) { int[] visited = new int[nums.length]; helper(0, nums, visited, new Stack<>()); return result; } private void helper(int depth, int[] nums, int[] visited, Stack<Integer> stack) { if (depth == nums.length) { result.add(new ArrayList<Integer>(stack)); return; } for (int i = 0; i < nums.length; ++i) { if (visited[i] == 1) continue; visited[i] = 1; stack.push(nums[i]); helper(depth + 1, nums, visited, stack); visited[i] = 0; stack.pop(); } }
5),LeetCode47: Full array II
Given a sequence that can contain repeating numbers, all non repeating permutations are returned.
Example:
Input: [1,1,2] Output: [ [1,1,2], [1,2,1], [2,1,1] ]
Explanation:
List<List<Integer>> result = new ArrayList<>(); public List<List<Integer>> permuteUnique(int[] nums) { int[] visited = new int[nums.length]; Arrays.sort(nums); helper(0, nums, visited, new Stack<>()); return result; } private void helper(int depth, int[] nums, int[] visited, Stack<Integer> stack) { if (depth == nums.length) { result.add(new ArrayList<Integer>(stack)); return; } for (int i = 0; i < nums.length; ++i) { if (visited[i] == 1) continue; if (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] != 1) continue; visited[i] = 1; stack.push(nums[i]); helper(depth + 1, nums, visited, stack); visited[i] = 0; stack.pop(); } }
6),LeetCode77: combination
Given two integers n and k, return 1... The combination of all possible k numbers in n
Example:
Input: n = 4, k = 2 Output: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
Explanation:
List<List<Integer>> result = new LinkedList<>(); public List<List<Integer>> combine(int n, int k) { helper(1, n, k, new LinkedList<Integer>()); return result; } private void helper(int first, int n, int k, LinkedList<Integer> list) { if (list.size() == k) { result.add(new LinkedList<Integer>(list)); return; } for (int i = first; i <= n; ++i) { list.add(i); helper(i + 1, n, k, list); list.removeLast(); } }
Time and space complexity of common data structures:
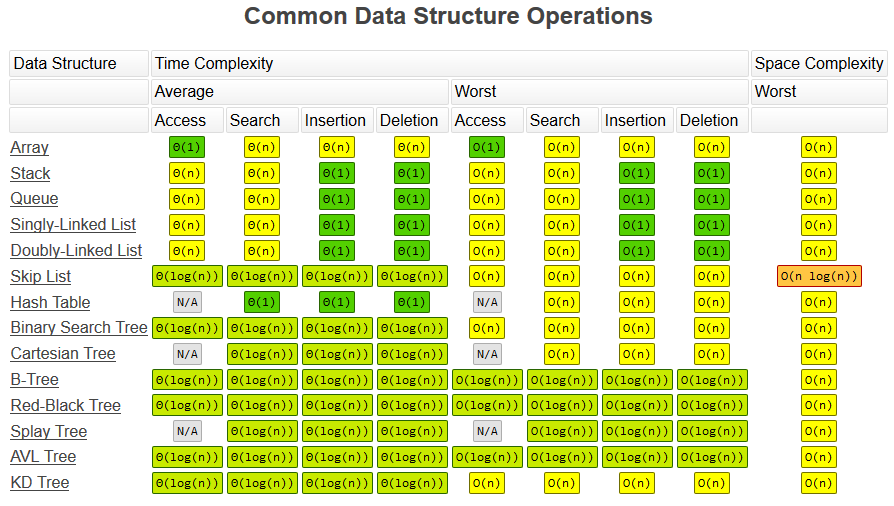
https://www.bigocheatsheet.com/