catalogue
1.2 summation of the first n items
1.3 Fibonacci sequence problem
1.3.1 Fibonacci sequence problem code
1.4 divide and conquer algorithm
1.6 chessboard coverage problem code
1 recursion
1.1 recursive definition
1. It usually transforms a large and complex problem layer by layer into a small-scale problem similar to the original problem. The recursive strategy can describe the multiple repeated calculations required in the problem-solving process with only a small amount of program, which greatly reduces the amount of code of the program.
2. Generally speaking, recursion needs boundary conditions, recursive forward segment and recursive return segment. When the boundary conditions are not satisfied, recursively advance; When the boundary conditions are met, it returns recursively.
1.2 summation of the first n items


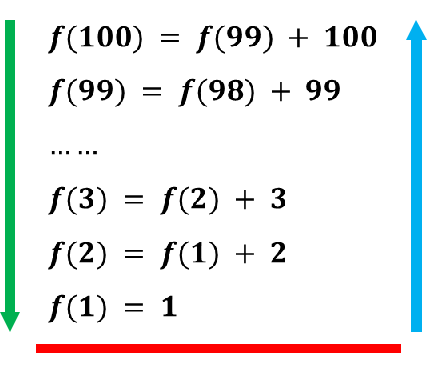
1.3 Fibonacci sequence problem


1.3.1 Fibonacci sequence problem code
package P4.Divide and conquer backtracking;
public class RecursionDemo03 {
public static void main(String[] args) {
int ret = f(50);
System.out.println(ret);
}
private static int f(int x) {
if (x == 1 || x == 2) {
return 1;
}
return f(x - 1) + f(x - 2);
}
}1.4 divide and conquer algorithm
Divide and conquer algorithm is to divide the original problem into n sub problems with small scale and similar structure to the original problem, solve these sub problems recursively, and then combine the results to obtain the solution of the original problem.
In the recursive implementation of divide and conquer algorithm, each layer of recursion involves three operations:
Decomposition: decompose the original problem into a series of sub problems
Solution: solve each subproblem recursively. If the subproblem is small enough, solve it directly
Merge: merge the results of sub problems into the original problem
The problems that divide and conquer algorithm can solve generally need to meet the following conditions:
The original problem has the same pattern as the small problem
The subproblems decomposed from the original problem can be solved independently, and there is no correlation between subproblems
With decomposition termination conditions, that is, when the problem is small enough, it can be solved directly
The subproblem can be merged into the original problem, and the complexity of this merging operation cannot be too high, otherwise it will not reduce the overall complexity of the algorithm
1.5 backtracking algorithm
Backtracking algorithm is actually a search attempt process similar to enumeration. It is mainly to find the solution of the problem in the search attempt process. When it is found that the solution conditions are not met, it will "backtrack" back and try other paths. Backtracking method is an optimization search method, which searches forward according to the optimization conditions to achieve the goal. However, when a certain step is explored and it is found that the original selection is not excellent or fails to achieve the goal, it will go back and choose again. This technology of going back and going again if it fails is called backtracking method, and the point in a certain state that meets the backtracking conditions is called "backtracking" point. Many complex and large-scale problems can use backtracking method, which is known as "general problem-solving method".
Go forward from one road. If you can enter, enter. If you can't enter, retreat. Try another road.
1.5 full arrangement
package P4.Divide and conquer backtracking;
import java.util.HashSet;
//Full arrangement
public class FullPermutation {
public static void main(String[] args) {
String s = "ABC";
char[] arr = s.toCharArray();
HashSet<String> set = new HashSet<>();
permutation(set ,arr,0,arr.length-1);
System.out.println(set);
}
private static void permutation(HashSet<String> set, char[] arr, int from, int to) {
if(from == to){
set.add(String.valueOf(arr));
}else {
for(int i = from; i<=to;i++){
swap(arr,i,from);
permutation(set,arr,from+1,to);
swap(arr,i,from);
}
}
}
private static void swap(char[] arr, int i, int from) {
char temp = arr[i];
arr[i] = arr[i];
}
}1.6 chessboard coverage
 1.6 chessboard coverage problem code
1.6 chessboard coverage problem code
package P4.Divide and conquer backtracking;
import java.util.Scanner;
//Chessboard coverage problem
public class ChessBoardCoverage {
private static int BOARD_SIZE = 8;
private static int[][] board = new int[BOARD_SIZE][BOARD_SIZE];
//The number of L dominoes representing the same color should be the same
private static int title = 0; // 0 is the existence of a special square
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.print(">>>Please enter the corner mark information of the special grid:");
//dr dc refers to the coordinates of a special grid
int dr = input.nextInt();
int dc = input.nextInt();
chessBoard(0, 0, dr, dc,BOARD_SIZE);
printBoard();
}
private static void printBoard() {
for (int i = 0; i < BOARD_SIZE; i++) {
for (int j = 0; j < BOARD_SIZE; j++) {
System.out.print(board[i][j] + "\t");
}
System.out.println();
}
}
//In the matrix of size*size, tr tc is the base point of the four part submatrix, and dr dc is the position of the special matrix for filling
private static void chessBoard(int tr, int tc, int dr, int dc, int size) {
//Judge the end of recursion. If the size is 1, it cannot continue to split and return to regression
if (size == 1) {
return;
}
//The layer to be filled with L-shaped dominoes has the same number
int num = ++title;
//The floor will continue to be divided into four parts. What is the size of each part
int s = size / 2;
//Which of the four parts is the special square
//Upper left
if (dr < tr + s && dc < tc + s) {
chessBoard(tr,tc,dr,dc,s);
} else {
board[tr + s - 1][tc + s - 1] = num;
chessBoard(tr,tc,tr + s - 1,tc + s - 1,s);
}
//Upper right
if (dr < tr + s && dc >= tc + s) {
chessBoard(tr,tc + s,dr,dc,s);
} else {
board[tr + s - 1][tc + s] = num;
chessBoard(tr,tc + s,tr + s - 1,tc + s,s);
}
//Lower left
if (dr >= tr + s && dc < tc + s) {
chessBoard(tr + s,tc,dr,dc,s);
} else {
board[tr + s][tc + s - 1] = num;
chessBoard(tr + s,tc,tr + s,tc + s - 1,s);
}
//lower right
if (dr >= tr + s && dc >= tc + s) {
chessBoard(tr + s,tc + s,dr,dc,s);
} else {
board[tr + s][tc + s] = num;
chessBoard(tr + s,tc + s,tr + s,tc + s,s);
}
}
}1.7 Hanoi Tower problem
The Hanoi Tower problem is an educational toy originated from an ancient Indian legend. When Brahma created the world, he made three diamond pillars. On one pillar, 64 gold discs were stacked in order of size from bottom to top. Brahma ordered Brahman to rearrange the disk on another pillar in order of size from below. It is also stipulated that the disc cannot be enlarged on the small disc, and only one disc can be moved between the three columns at a time.
package P4.Divide and conquer backtracking;
//Problems with known established laws
//Problems with unknown established laws
public class Hanoi {
public static void main(String[] args) {
String x = "X";
String y = "Y";
String z = "Z";
hanoi(3,x,y,z);
}
private static void hanoi(int n, String begin, String mid, String end) {
if (n == 1) {
System.out.println(begin + "->" + end);
} else {
hanoi(n - 1,begin, end, mid);
System.out.println(begin + "->" + end);
hanoi(n - 1,mid, begin, end);
}
}
}1.8 maze problem
package P4.Divide and conquer backtracking;
import P3.Chain structure.LinkedList;
public class Maze {
private static int[][] maze = {
{1, 1, 1, 1, 1, 1, 1, 1, 1},
{0, 0, 1, 0, 0, 0, 1, 1, 1},
{1, 0, 1, 1, 1, 0, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 1, 1, 1},
{1, 1, 0, 1, 1, 0, 0, 0, 1},
{1, 0, 0, 0, 0, 0, 1, 0, 1},
{1, 0, 1, 1, 1, 0, 0, 0, 1},
{1, 1, 0, 0, 0, 0, 1, 1, 0},
{1, 1, 1, 1, 1, 1, 1, 1, 1}
};
//Entry information
private static int entryX = 1;
private static int entryY = 0;
//Export information
private static int exitX = 7;
private static int exitY = 8;
//Path access status table
private static boolean[][] vistied = new boolean[9][9];
//Change in direction
private static int[][] direction = {
{-1, 0}, {0, 1}, {1, 0}, {0, -1}
};
//Stack of storage paths
private static LinkedList<String> stack = new LinkedList<>();
public static void main(String[] args) {
boolean flag = go(entryX, entryY);
if (flag) {
for (String path : stack) {
System.out.println(path);
}
} else {
System.out.println("The maze is impassable!");
}
}
//Take X and y as the entry to see if the exit can be found downward. Return false and cannot be found
private static boolean go(int x, int y) {
stack.push("(" + x + "," + y + ")");
vistied[x][y] = true;
if (x == exitX && y == exitY) {
return true;
}
//Consider four directions: top right, bottom left
for (int i = 0; i < direction.length; i++) {
int newX = direction[i][0] + x;
int newY = direction[i][1] + y;
if (isInArea(newX, newY) && isRoad(newX, newY) && !vistied[newX][newY]) {
if(go(newX,newY)) {
return true; //If a direction can pass, return true upward, indicating that X and y of this level can pass
}
}
}
stack.pop();
return false; //If none of the four directions is available, false will be returned upward, indicating that X and Y layers are unavailable this time
}
private static boolean isRoad(int x, int y) {
return maze[x][y] == 0;
}
private static boolean isInArea(int x, int y) {
return x >= 0 && x < 9 && y >=0 && y < 9;
}
}1.9N queen problem
In an 8 × Eight Queen pieces shall be placed in the chessboard of 8. It is required that there shall be no duplicate queen pieces in the same row with the same oblique line
package P4.Divide and conquer backtracking;
//N-queens problem
public class NQueen {
private static int count = 0; //Record the number of solutions
private static final int N = 8; //Size of N-queen matrix
private static int[][] arr = new int[N][N]; //Chessboard data 0 means empty and 1 means queen
public static void main(String[] args) {
queen(0);
}
//Recursively solve the problem of row subscript row queen. If row == N, a solution will come out
private static void queen(int row) {
if (row == N) {
count++;
System.out.println("The first" + count + "Solutions:");
printArr();
} else {
//Traverses the columns of the current row
for (int col = 0; col < N; col++) {
if (!isDangerous(row, col)) {
//Each time you want to place a queen, empty the row first
for (int c = 0; c < N; c++) {
arr[row][c] = 0;
}
arr[row][col] = 1;
queen(row + 1);
}
}
}
}
private static boolean isDangerous(int row, int col) {
//Up
for (int r = row - 1; r >= 0; r--) {
if (arr[r][col] == 1) {
return true;
}
}
//Upper left
for (int r = row - 1, c = col - 1; r >= 0 && c >= 0; r--, c--) {
if (arr[r][c] == 1) {
return true;
}
}
//Upper right
for (int r = row - 1, c = col + 1; r >= 0 && c < N; r--, c++) {
if (arr[r][c] == 1) {
return true;
}
}
return false;
}
private static void printArr() {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
}
1.10 Sudoku problem
The numbers in each row, column and thick line Palace (3 * 3) contain 1-9 and are not repeated
package P4.Divide and conquer backtracking;
import java.io.*;
//Sudoku
public class Sudoku {
private static int i = 0;
private static int[][] board = new int[9][9];
public static void main(String[] args) throws IOException {
readFile("sudoku_data_01.txt");
solve(0, 0);
}
//Solve the solution of x-y lattice, and then continue to solve the next lattice recursively
//Essence seeks multiple solutions, but the actual Sudoku problem can only have one solution. If there is no solution, the program will not output anything!
private static void solve(int row, int col) {
if (row == 9) {
i++;
System.out.println("===========" + i + "==========");
printBoard();
//System.exit(0);
} else {
if (board[row][col] == 0) {
//You need to fill in numbers 1 ~ 9
for (int num = 1; num <= 9; num++) {
if (!isExist(row, col, num)) {
board[row][col] = num; //8
//Solve the next grid
solve(row + (col + 1) / 9, (col + 1) % 9);
}
//If there is no solution here, it must be cleared
board[row][col] = 0;
}
} else {
//There is already a known number. Jump directly to the next grid
solve(row + (col + 1) / 9, (col + 1) % 9);
}
}
}
private static boolean isExist(int row, int col, int num) {
//Peer
for (int c = 0; c < 9; c++) {
if (board[row][c] == num) {
return true;
}
}
//Same column
for (int r = 0; r < 9; r++) {
if (board[r][col] == num) {
return true;
}
}
//Same as Jiugong 3 * 3
int rowMin = 0;
int colMin = 0;
int rowMax = 0;
int colMax = 0;
if (row >= 0 && row <= 2) {
rowMin = 0;
rowMax = 2;
}
if (row >= 3 && row <= 5) {
rowMin = 3;
rowMax = 5;
}
if (row >= 6 && row <= 8) {
rowMin = 6;
rowMax = 8;
}
if (col >= 0 && col <= 2) {
colMin = 0;
colMax = 2;
}
if (col >= 3 && col <= 5) {
colMin = 3;
colMax = 5;
}
if (col >= 6 && col <= 8) {
colMin = 6;
colMax = 8;
}
for (int r = rowMin; r <= rowMax; r++) {
for (int c = colMin; c <= colMax; c++) {
if (board[r][c] == num) {
return true;
}
}
}
return false;
}
private static void readFile(String fileName) throws IOException {
File file = new File(fileName);
FileReader fr = new FileReader(file);
BufferedReader br = new BufferedReader(fr);
String line = null;
int row = 0;
while ((line = br.readLine()) != null) {
for (int col = 0; col < 9; col++) {
board[row][col] = Integer.parseInt(line.charAt(col) + "");
}
row++;
}
}
private static void printBoard() {
for (int i = 0 ; i < 9; i++) {
for (int j = 0; j < 9; j++) {
System.out.print(board[i][j] + " ");
}
System.out.println();
}
}
}