The "Divide and Conquer" in the algorithm is to divide a large problem into small problems, break them one by one, and "Divide and Conquer".

The specific operation of divide and conquer algorithm is to divide the original problem into # k # smaller subproblems and solve these # k # subproblems respectively. If the subproblem is not small enough, each subproblem is divided into smaller subproblems. This decomposition continues until the problem is small enough to easily find the solutions of these small problems.

The topic of divide and conquer has two characteristics:

1. Balance subproblem: the subproblem has roughly the same scale. The problem can be divided into two subproblems of almost equal size, i.e. k = 2. When coding, it is divided into two parts at a time, and then continue to be divided into two parts. This step is very similar to dichotomy. Of course, dichotomy is also a divide and conquer method, but the application of dichotomy is very simple.
2. Independent subproblems: subproblems are independent of each other. This is the fundamental feature different from dynamic programming algorithm. In dynamic programming algorithm, subproblems are interrelated rather than independent

Divide and conquer can optimize the complexity of the algorithm and turn O(n) into O(logn)

When establishing the model with divide and conquer method, the problem-solving steps are divided into three steps:

1. Divide: decompose the problem into independent subproblems;
2. Conquer: solve subproblems recursively;
3. Combine: combine the results of the subproblem into the solution of the original problem.

 

Hanoi Tower - Blue Bridge cloud course (lanqiao.cn)

Its logic is very simple. The problem of moving n − plates is divided into two n − 1 subproblems. There are three columns x, y and z ， and the initial ， n ， plates are on ， x ，.  

#include<bits/stdc++.h>
using namespace std;
int sum = 0, m;
void hanoi(char x,char y,char z,int n){  //Three columns x, y, z
    if(n==1) {                           //Minimum problem
        sum++;
        if(sum==m) cout<<"#"<<n<<": "<<x<<"->"<<z<<endl;
    }
    else {                               //Divide and conquer
        hanoi(x,z,y,n-1); //(1) First move the n-1 small disk of x to y, and then move the n-th large disk to z
        sum++;
        if(sum==m) cout<<"#"<<n<<": "<<x<<"->"<<z<<endl;
        hanoi(y,x,z,n-1); //(2) Move the n-1 disk of y to z
    }
}
int main(){
    int n;    cin>>n>>m;
    hanoi('A','B','C',n);
    cout<<sum<<endl;
    return 0;
}

 Fast power blue bridge cloud course (lanqiao.cn)

Used a little math, I don't understand

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll fastPow(ll a, ll n,ll m){           //a^n mod m
    if(n == 0)   return 1;             //Special judgment a^0=1
    if(n == 1)   return a;
    ll temp = fastPow(a, n/2,m);       //Divide and conquer
    if(n%2 == 1)                       //Odd a. It can also be written like this: if (n & 1)
        return temp * temp % m * a % m;
    else                               //Even a.
        return temp * temp % m ;
}
int main(){
    ll b,p,k;
    cin >> b >>p>>k;
    printf("%lld",fastPow(b,p,k));
    return 0;
}

Reverse order pair - Blue Bridge cloud course (lanqiao.cn)

Let's introduce merge sort first. The following figure shows the operation steps of merge sort. After {3} times merging of the initial sequence, an ordered sequence from small to large is obtained.

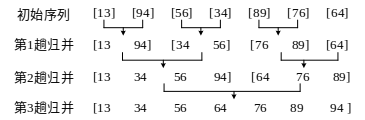
It is not difficult to find that the main operations of merging and sorting are:

1. Decomposition. Divide the initial sequence into two left and right subsequences with the same length, and then divide each subsequence into two smaller subsequences... Until the subsequence contains only ， 1 ， numbers. This process is implemented recursively. The first line in the figure above is the initial sequence, and each number is a subsequence, which can be regarded as the lowest level of recursion.
2. Solve the sub problem and sort the sub sequence. The lowest subsequence only contains 1 # numbers, which can be sorted without sorting.
3. Merge. Merge 22} ordered subsequences, which is the main operation of merge sorting. For example, in the figure below, I} and {j} point to the {11th} number of subsequences {13, 94, 99} and {34, 56} respectively. For the first comparison, it is found that {a[i] < a [j], and a[i] is placed in the temporary space {b []. After four comparisons, we get {b [] = {13, 34, 56, 94, 99}.

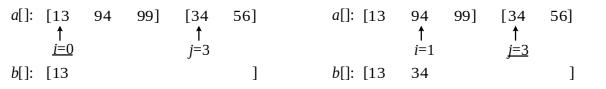
(a) 1st comparison (b) 2nd comparison

 

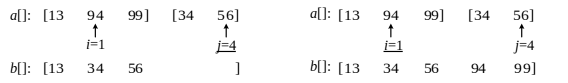
Merge and sort the number of # n #:

• Need to merge logn times;
• In each merge, there are many merge operations, requiring a total of {O(n) comparisons

So the time complexity is O(nlogn).

There are two standard solutions to this problem. One is

There are two standard solutions to this problem, one is a tree array, and the other is merging and sorting.

As long as the records are in reverse order in the process of merging and sorting

#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
typedef  long  long  ll;
int a[N], b[N];
ll cnt;
void Merge(ll l, ll mid, ll r){
     ll i=l, j = mid+1, t=0;
     while(i <= mid && j <= r){
          if(a[i] > a[j]){
               b[t++] = a[j++];
               cnt += mid-i+1;                //Record the number of pairs in reverse order
          }
          else b[t++]=a[i++];
     }
   //If the number in one subsequence has been processed and the other has not been processed, copy the rest directly:
    while(i <= mid)   b[t++]=a[i++];
    while(j <= r)     b[t++]=a[j++];
    for(i=0; i<t; i++)  a[l+i] = b[i];     //Copy the ordered b [] back to a []
}
void Mergesort(ll l, ll r){
    if(l<r){
         ll  mid = (l+r)/2;                   //Bisect into two subsequences
         Mergesort(l, mid);
         Mergesort(mid+1, r);
         Merge(l, mid, r);                    //merge
    }
}
int main(){
    int n,k;
    cin >>n;
    cnt = 0;
    for(int i=0;i<n;i++)  scanf("%d", &a[i]);
    Mergesort(0,n-1);                     //Merge sort
    cout <<cnt;
    return 0;
}

Sorting - Blue Bridge cloud course (lanqiao.cn) 

Introduce the idea of fast platoon by using fast platoon:

Divide the sequence into left and right parts so that all the numbers on the left are smaller than those on the right; Recurse this process until it can no longer be divided.

 

The complexity is calculated by merging and sorting.

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int a[N];
void quick_sort(int l, int r){    //left, right
    int i = l, j = r;
    int mid = (l + r) >> 1;       //mid = (l + r)/2
    int x = a[mid];
    while(i <= j){
        while(i <= j && a[i] < x)    i++;
        while(i <= j && a[j] > x)    j--;
        if(i <= j){
            swap(a[i], a[j]);
            i++, j--;
        }
    }
    if(l < j)    quick_sort(l, j);
    if(i < r)    quick_sort(i, r);
}

int main(void){
    int n;
    scanf("%d", &n);
    for(int i = 0;i < n;i++)
        scanf("%d", &a[i]);
    quick_sort(0, n - 1);
    for(int i = 0;i < n;i++)   printf("%d ", a[i]);
    printf("\n");
    for(int i = n-1;i >=0;i--) printf("%d ", a[i]);
    printf("\n");
    return 0;
}