The Idea of Dividing and Treating
Score - break down the problem into smaller subproblems;
Fix - Fix these smaller subproblems one by one;
Combine - Combine the solved sub-problems to get the solution of the "mother" problem.
Merge Sort
If there is an array A[0...n]
Break up the array until there are only two elements left
Merging decimal arrays while sorting (called merging)
Merge all the way to the original array.
The key is three points:
- How to decompose
- How to merge
Decomposition:
Method 1: Build a binary tree. After building, traverse in postorder (that is, left subtree-right subtree-root)
. Implemented recursively.
Method 2: Directly decompose into two elements without building a tree or recursion at all.
Merge:
Use a similar way of rolling table. We call the two decimal arrays to be merged left and right.
Contrast one by one on the left and one on the right. Whoever is small will be placed in rows one by one.
Merge Sort Practice
Example:
A = [3, 7, 6, 7, 8, 6, 2, 9]
Sort A by Merge
Step 1: Decomposition
As shown in the figure, keep dividing until there are only two elements left.
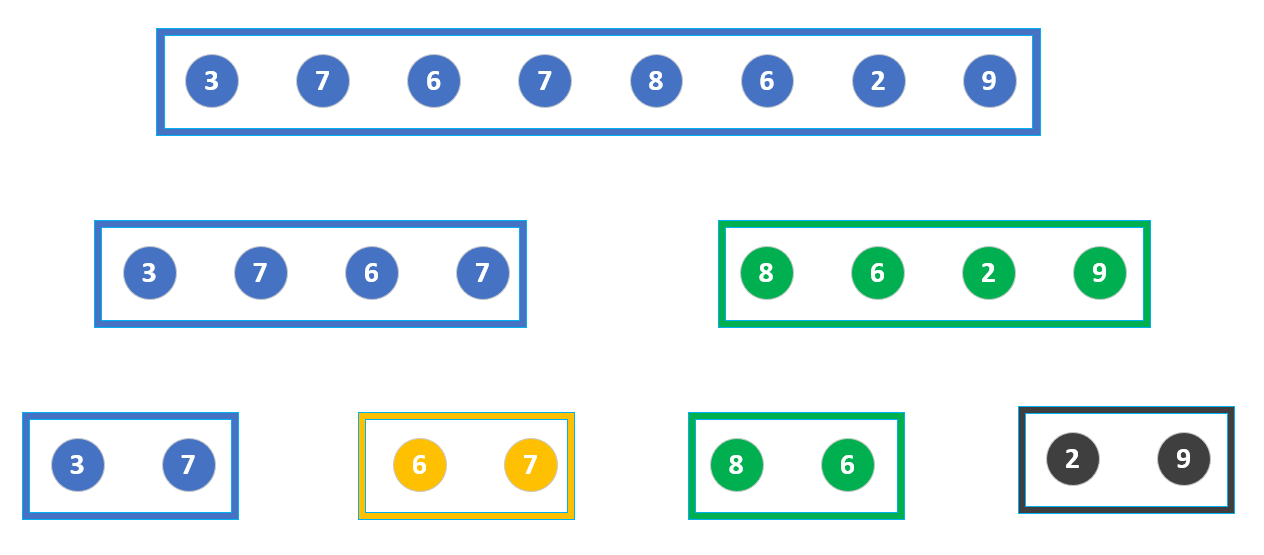
Suppose we decompose in the first way. The above image corresponds to a tree.
Build a tree by using post-order traversal: When you build a tree, if you don't, it keeps forking to the left. When the left bifurcates to the bottom, the right bifurcates. When both the left and right forks are at the end, return to the root.
The flow of post-traversal is as follows:
- Are the left bifurcations all there? (that is, can the current node continue to bifurcate to the left?) If not, continue with the left bifurcation
- Are the right bifurcations all there? (that is, can the current node continue to branch to the right?) If not, continue with right bifurcation
- If not, then go back to the root (that is, back to the previous level)

We build the tree recursively.
Writing recursion has two main meanings:
- What is the termination condition? (When do you exit?)
- What are recursion conditions? (When does it split?)
Recursive functions can always be boiled down to a template, such as the following pseudocode:
def Recursive function ( a,b,c): if(Termination condition met) return (xxx) Recursive function ( a1,b1,c1) Recursive function ( a1,b1,c1) Bottom-up duplicate operation
There are several forks, and the recursive function writes a few, so build a binary tree here so write two.
Where return xxx can also simply return empty
Where "if (satisfies the termination condition) return xxx" can also be written as
def Recursive function ( a,b,c): if(Termination condition not met) Recursive function ( a1,b1,c1) Recursive function ( a1,b1,c1) Bottom-up duplicate operation
So let's apply the template to get decomposed pseudocode written recursively
def sort(A, lo, hi): if(lo>=hi):#Termination Conditions return mid = int((lo+hi)/2) sort(A, lo, mid) #Left Bifurcation sort(A, mid+1, hi) #Right Bifurcation merge(A, lo, hi) #Merge operation, explained in the next section
Where the termination condition is lo>=hi, which means to return when there is only one element left, but to do nothing at that time, just to return. So the bottom-most operation is actually done on the second-to-last layer after returning. To prevent confusion, we assume that the second last layer to come back is the bottom. At this point, there are only two elements at the bottom.
Where lo and hi represent the first and last position of the undissolved group, as shown in the figure,
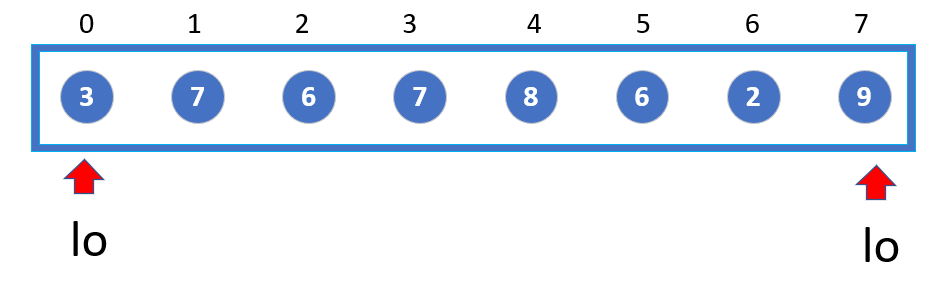
Divide it in the middle and get groups A[lo...mid] and A[mid+1...hi]
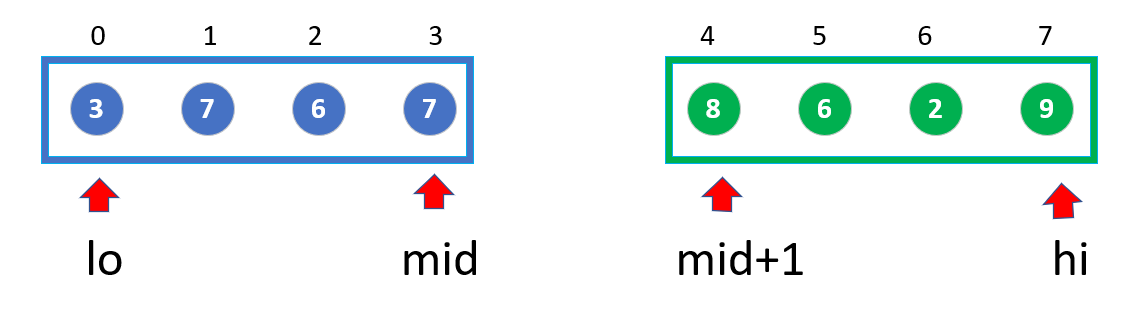
At this point, the decomposition is complete, and the bottom-most array we get is:

These four small arrays are two in length.
Step 2: Merge
We're going to merge like a rolling table, and who's the youngest is selected in the ranked array.
Before we can actually sort, we must first define a temporary array.
Define Temporary Array
So let's first define a temporary array to place the arranged array.
Such as defining
ordered = []
Used to store arranged arrays
Do something, then put an element a, into ordered
ordered.append(a)
When you're done, return to the ordered array.
The problem with this is that the function passes an ordered array over and over again. A better alternative is to pass only the array A and place the arranged elements in A. But then the original A will be overwritten. So in order not to lose the original A, request a temporary array tmp to store the original A. tmp does not need to be passed, because when sorting is complete, we only need the ordered array A, and tmp can be discarded.
tmp: An array of length n used to store the original A
A: A sorted array that is constantly updated during the process.
At the beginning of the merge function, copy A to tmp first
for i in range(n): tmp[i] = A[i]
Rolling sort
Then you can start sorting.
Start rolling now!
First introduce the rules:
- From scratch, one element on each side for 1v1 PK
- The PK method is: Whoever is younger is scratched out and selected into array A; Whoever is older will remain to continue PK
- If one of the teams is empty, then the other element is directly selected in array A
So the sign of victory is who wins. It is an honor to be selected A.
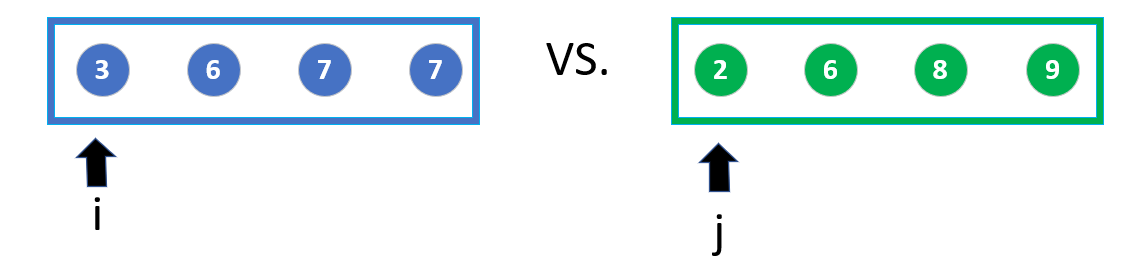
To mark who is scratched and who is left, we define two subscripts: i and j.
- I indicates who the elements of the left team (blue side) are currently on the platform (their subscripts). Before i, they were scratched out and selected as A. After i, they have not been on the platform yet.
- Similarly, j indicates who the elements of the right team are currently on the rolling table.
Next, introduce two teams:
Left (blue side): [3, 6, 7, 7]
Right (green side): [2, 6, 8, 9]
The line-up before the game was like this:
Everything is ready,
Start the game!
The first is the ratio of 3 to 2. 2 small, selected A.

We move the subscript j

3 You still need to stay on the race platform.
Start the next round:
At this time, the blue side dispatched 3 rounds, pulled back a round, was selected A!

Move Subscript i
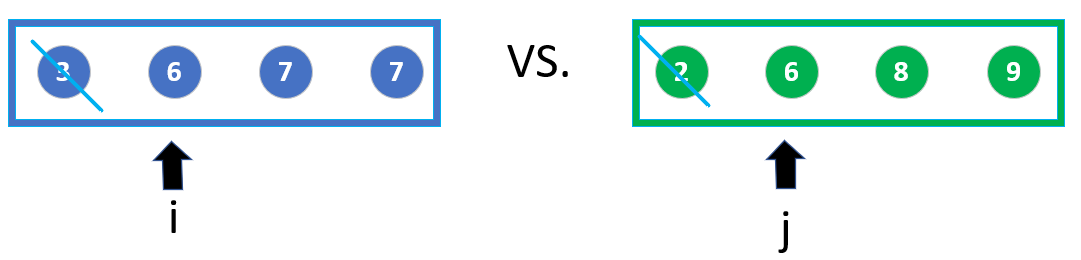
Start the third round:
Blue side is 6, green side is 6, draw! You can choose any one at this time, so let's choose the blue side.

Move Subscript i

Start the fourth round:
The blue side is 7 and the green side is 6. Green is selected as A

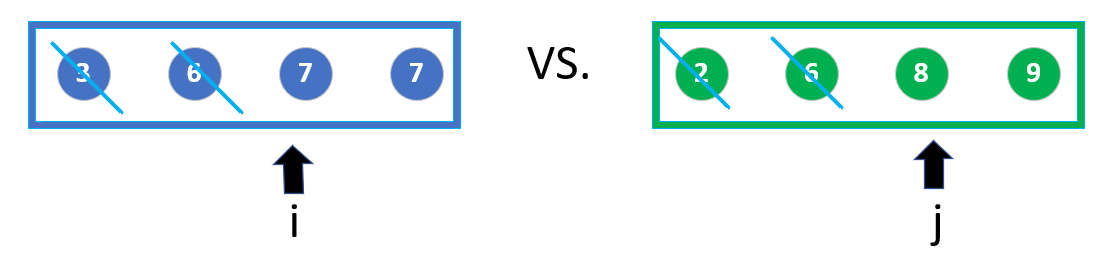
Start the fifth round:
Green sent 8 instead of 7


Start the sixth round:
Blue sent another 7 and won again

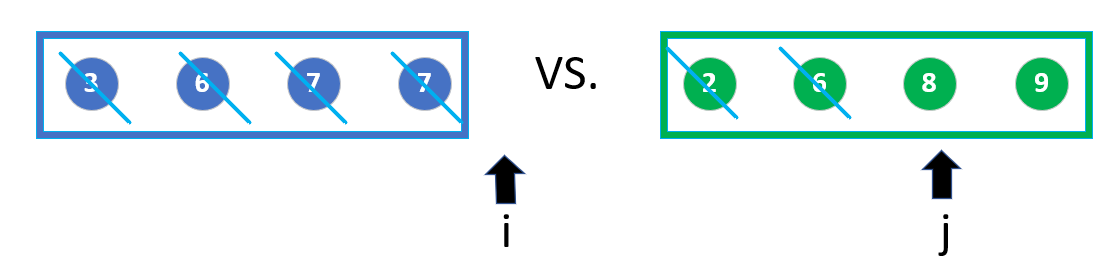
At this time, all the elements of the Blue Team have been selected as A!
The game is over. The other two players of the blue team, just put in A one by one.
The end result is:

How can I ensure order within subgroups?
As we can see, while rolling, the two arrays are synthesized into an array A, which is ordered.
But there is one thing I intentionally did not mention: the two subgroups themselves are ordered!
This is a prerequisite for the race!
How can this be guaranteed?
As long as you go from bottom to top, make sure that you are in order before you go up each time. Naturally, the two subgroups are in order!
From the bottom, you can still compare them by rolling tables, but there are only two elements, 1v1. After the race, an orderly subgroup will naturally be merged and moved up to 2v2. Then the four rollers are merged into an ordered array. Go up again is 4v4. This is repeated until it is merged into the original array.
So the answer is, as long as they are merged bottom-up, there must be order within the subgroups. In other words, we don't need to do anything, it's just orderly.
Merged code implementation
The pseudocode is as follows
def merge(A, lo, hi): mid = int((lo + hi)/2) #Last position of left subgroup for k in range(lo, hi): #Copy to tmp tmp[k] = A[k] for k in range(lo, hi): if(i>mid): A[k] = tmp[j++] #If left is empty, select right elif(j>hi): A[k] = tmp[i++] #If the right side is empty, select the left side elif(A[i]<=A[j]): A[k] = tmp[i++] #If the left side is small, select the left side else: A[k] = tmp[j++] #If the right side is small, select the right side
Code reference from Algorithm4
Extension: Add only two lines to invert ordinals
cnt = 0 def merge(A, lo, hi): mid = int((lo + hi)/2) #Last position of left subgroup for k in range(lo, hi): #Copy to tmp tmp[k] = A[k] for k in range(lo, hi): if(i>mid): A[k] = tmp[j++] #If left is empty, select right elif(j>hi): A[k] = tmp[i++] #If the right side is empty, select the left side elif(A[i]<=A[j]): A[k] = tmp[i++] #If the left side is small, select the left side else: A[k] = tmp[j++] #If the right side is small, select the right side cnt += mid - i +1 #cnt is an inverse ordinal number, mid-i+1 is the distance between I and mid
Final Code: Inverse Ordinal
cnt = 0
def merge(A, lo, hi):
mid = int((lo + hi)/2) #Last position of left subgroup
tmp=[]
for k in range(lo, hi): #Copy to tmp
tmp[k] = A[k]
for k in range(lo, hi):
if(i>mid): A[k] = tmp[j]; j+=1 #If left is empty, select right
elif(j>hi): A[k] = tmp[i]; i+=1 #If the right side is empty, select the left side
elif(A[i]<=A[j]): A[k] = tmp[i]; i+=1 #If the left side is small, select the left side
else:
A[k] = tmp[j]; j+=1 #If the right side is small, select the right side
cnt += mid - i +1 #cnt is an inverse ordinal number, mid-i+1 is the distance between I and mid
def sort(A, lo, hi):
if(lo>=hi):#Termination Conditions
return
mid = int((lo+hi)/2)
sort(A, lo, mid) #Left Bifurcation
sort(A, mid+1, hi) #Right Bifurcation
merge(A, lo, hi) #Merge operation, explained in the next section
A = [3, 7, 6, 7, 8, 6, 2, 9]
sort(A, 0, len(A)-1) #External call
print('Inverse ordinal number',cnt)