preface
Today I see a topic: Inverse Polish expression evaluation , as follows:
Find the value of the expression according to the inverse Polish representation.
Valid operators include +, -, *, /. Each operand can be an integer or another inverse expression.
explain:
Integer division preserves only the integer part.
The given inverse Polish expression is always valid. In other words, an expression always yields a valid value and there is no case where the divisor is 0.
Example 1:
Input: tokens = ["2","1","+","3", "*"]
Output: 9
Explanation: this expression is transformed into a common infix arithmetic expression: ((2 + 1) * 3) = 9
Example 2:
Input: tokens = ["4","13","5", "/", "+"]
Output: 6
Explanation: this expression is transformed into a common infix arithmetic expression: (4 + (13 / 5)) = 6
Example 3:
Input: tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5", "+"]
Output: 22
Explanation:
This expression is transformed into a common infix arithmetic expression as follows:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
answer
In fact, this problem is not difficult. You can use the stack.
The inverse Polish expression strictly follows the operation of "left to right". When calculating the value of the inverse Polish expression, use a stack to store operands, traverse the inverse Polish expression from left to right, and perform the following operations:
If an operand is encountered, the operand is put on the stack;
If an operator is encountered, the two operands will be out of the stack. The right operand will be out of the stack first, and the left operand will be out of the stack later. Use the operator to operate the two operands and put the new operand obtained by the operation into the stack.
After traversing the entire inverse Polish expression, there is only one element in the stack, which is the value of the inverse Polish expression.
Faced with this simple problem, I hit hard and wrote the following code:
1 class Solution(object): 2 def evalRPN(self, tokens): 3 """ 4 :type tokens: List[str] 5 :rtype: int 6 """ 7 data_stack = [] 8 for i in tokens: 9 if i not in ['+', '-', '*', '/']: 10 data_stack.append(int(i)) 11 else: 12 b = data_stack.pop() 13 a = data_stack.pop() 14 if i == '+': 15 res = a + b 16 elif i == '-': 17 res = a - b 18 elif i == '*': 19 res = a * b 20 else: 21 res = a // b 22 data_stack.append(res) 23 return data_stack[-1]
The first two test cases are tested, passed, perfect, submitted, oh, wrong, the wrong case is just the third test case.
I thought something was wrong, so I printed the calculation process of each step and finally found the problem
When calculating 6 / - 132, the answer given in the problem solution is:
6 / -132 = 0
But my answer is
6 / / - 132 = - 1 (python's "/" is the real division, which is generally rounded with "/")
Therefore, today's problem is introduced.
python3
- True Division:/
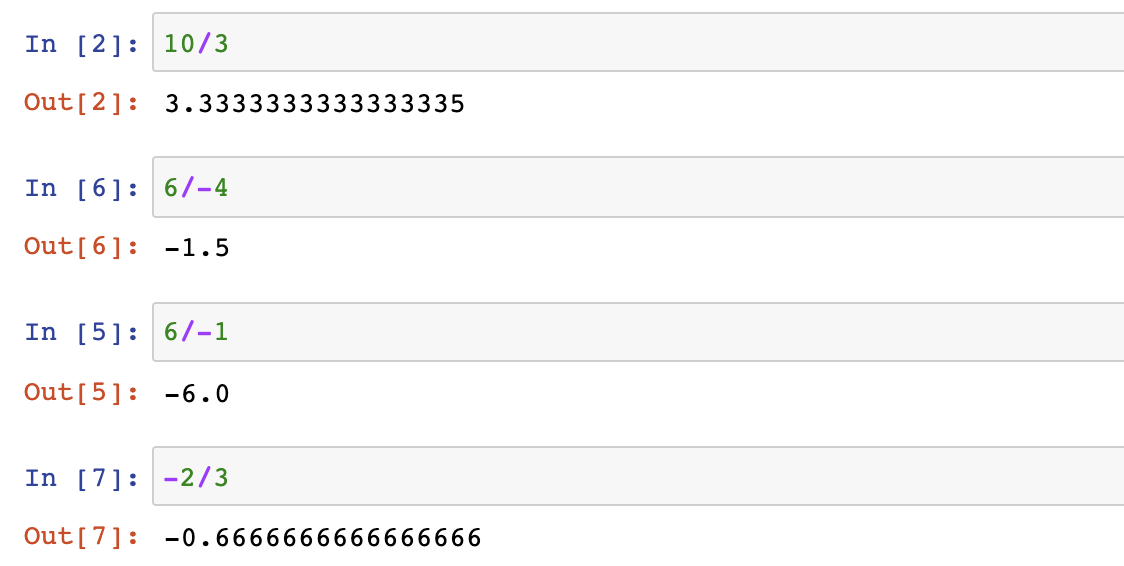
- The floor is rounded down / /
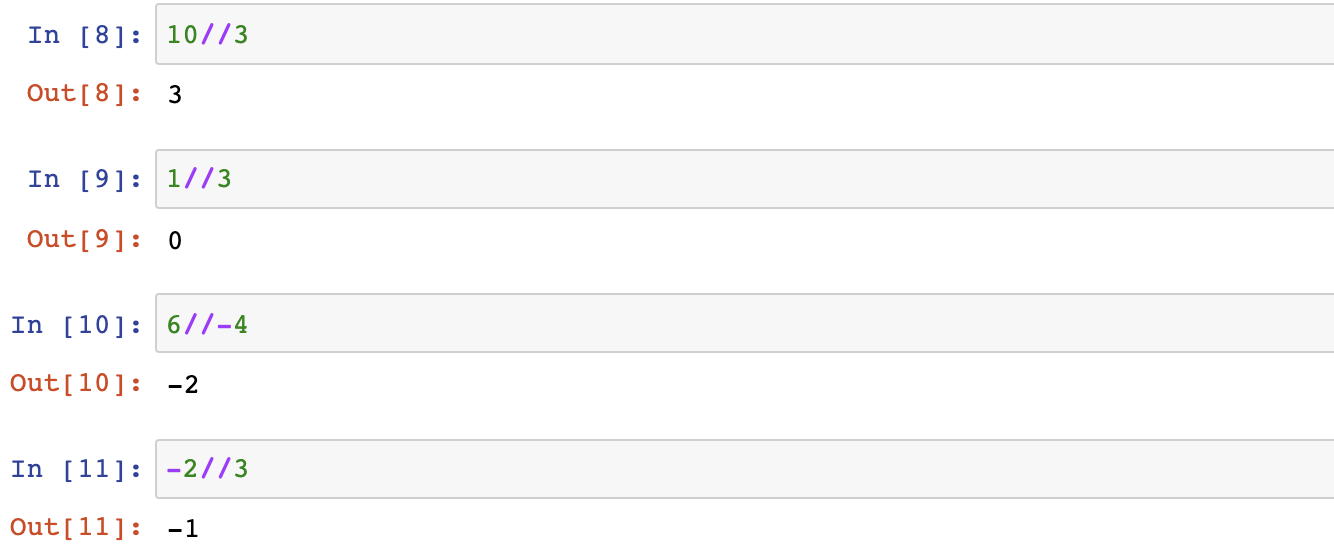
- int() directly truncates} decimals and rounds them. Violent truncation is used. Positive numbers and negative numbers are different. Pay attention to the difference between / /
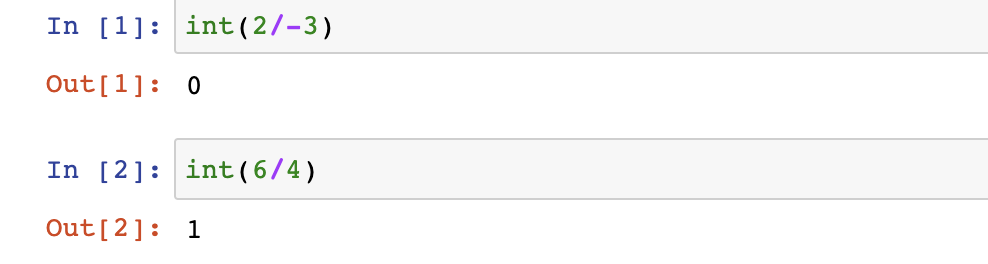
- math.ceil() round up

math.floor() rounded down

Java
1 public class TestDivide { 2 public static void main(String[] args) { 3 System.out.println("Intercept integer part"); 4 System.out.println("1 / 3 = " + 1 / 3); 5 System.out.println("6 / 3 = " + 6 / 3); 6 System.out.println("6 / 4 = " + 6 / 4); 7 System.out.println("-3 / 2 = " + -3 / 2); 8 9 System.out.println("True Division"); 10 System.out.println("1.0 / 3 = " + 1.0 / 3); 11 System.out.println("6.0 / 3 = " + 6.0 / 3); 12 System.out.println("6.0 / 4 = " + 6.0 / 4); 13 System.out.println("-3.0 / 2 = " + -3.0 / 2); 14 15 System.out.println("Round up"); 16 System.out.println("Math.ceil(-1.1) = " + Math.ceil(-1.1)); 17 System.out.println("Math.ceil(-1.5) = " + Math.ceil(-1.5)); 18 System.out.println("Math.ceil(1.1) = " + Math.ceil(1.1)); 19 System.out.println("Math.ceil(1.5) = " + Math.ceil(1.5)); 20 21 System.out.println("Round down"); 22 System.out.println("Math.floor(-1.1) = " + Math.floor(-1.1)); 23 System.out.println("Math.floor(-1.5) = " + Math.floor(-1.5)); 24 System.out.println("Math.floor(1.1) = " + Math.floor(1.1)); 25 System.out.println("Math.floor(1.5) = " + Math.floor(1.5)); 26 } 27 }
The results are as follows:
>>> Intercept integer part 1 / 3 = 0 6 / 3 = 2 6 / 4 = 1 -3 / 2 = -1 True Division 1.0 / 3 = 0.3333333333333333 6.0 / 3 = 2.0 6.0 / 4 = 1.5 -3.0 / 2 = -1.5 Round up Math.ceil(-1.1) = -1.0 Math.ceil(-1.5) = -1.0 Math.ceil(1.1) = 2.0 Math.ceil(1.5) = 2.0 Round down Math.floor(-1.1) = -2.0 Math.floor(-1.5) = -2.0 Math.floor(1.1) = 1.0 Math.floor(1.5) = 1.0
Go
1 import ( 2 "fmt" 3 "math" 4 ) 5 6 func main() { 7 x := 1.1 8 fmt.Println(1 / 2) // 0 9 fmt.Println(1 / 3) // 0 10 fmt.Println(-1 / 3) // 0 11 fmt.Println(-4 / 5) // 0 12 13 fmt.Println(1.0 / 2) // 0.5 14 fmt.Println(1.0 / 3) // 0.33333333333 15 fmt.Println(-1.0 / 3) // -0.333333333333 16 fmt.Println(-4.0 / 5) // -0.8 17 18 fmt.Println(math.Ceil(x)) // 2 19 fmt.Println(math.Floor(x)) // 1 20 }