This article is shared from Huawei cloud community< Do you really understand the five basic data structures of Redis? You may need to take a look at these knowledge points >, author: Li Ziba.
1, Introduction
All data structures in Redis obtain the corresponding value data through a unique string key.
Redis has five basic data structures:
- String (string)
- list
- hash (Dictionary)
- set
- zset (ordered set)
Among them, list, set, hash and zset are container data structures, which share the following two general rules:
- create if not exists: create if the container does not exist
- drop if no elements: if there are no elements in the container, delete the container immediately to free memory
This article will describe in detail the five basic data structures of Redis.
2, String (string)
1. Introduction to string
1.1 internal structure of string
String (string) is the simplest and most widely used data structure in Redis. Its interior is a character array. As shown in the figure:
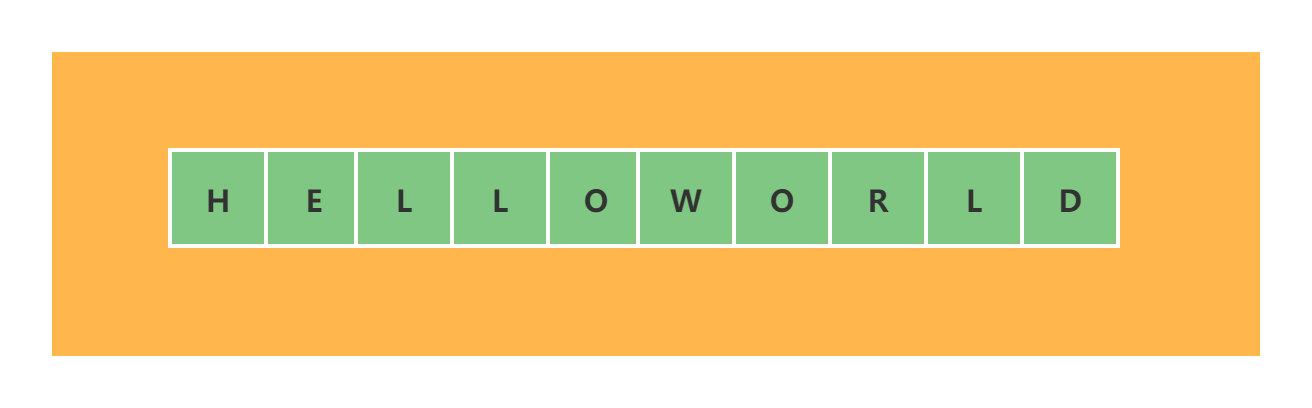
String in Redis is a dynamic string and can be modified; Its structural implementation is similar to ArrayList in Java (an initial array with a size of 10 is constructed by default), which is the idea of redundant memory allocation, also known as pre allocation; This idea can reduce the performance consumption caused by capacity expansion.
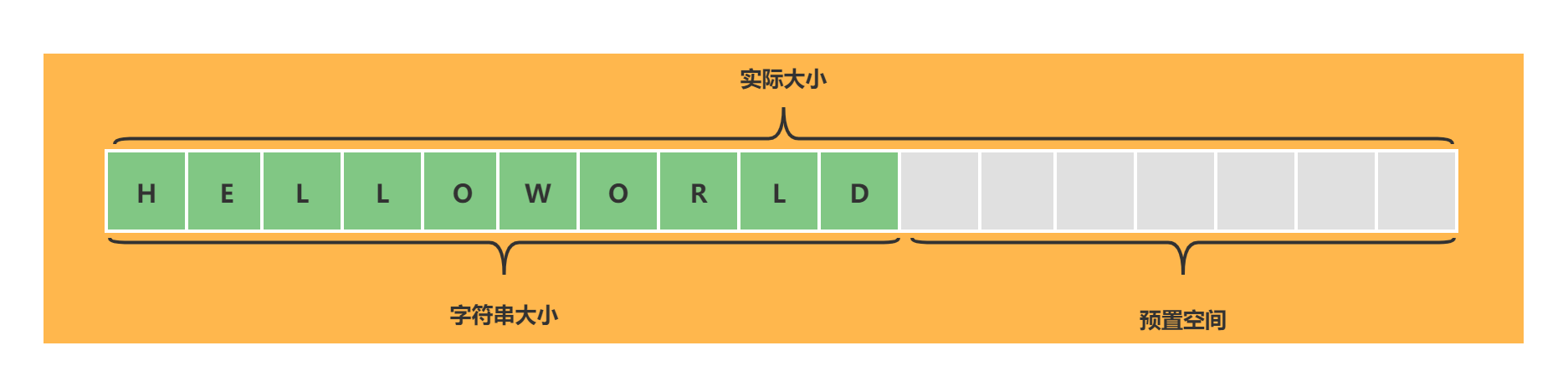
1.2 expansion of string
When the size of string reaches the capacity expansion threshold, the capacity of string will be expanded. The capacity expansion of string mainly includes the following points:
- The length is less than 1MB, which is twice the original after capacity expansion; length = length * 2
- If the length is greater than 1MB, 1MB will be added after capacity expansion; length = length + 1MB
- The maximum length of the string is 512MB
2. String (string) instruction
2.1 adding, deleting, modifying and querying a single key value pair
Set - > key is added if it does not exist, and modified if it exists
set key valueGet - > query and return the value of the corresponding key. If there is no return (nil)
get keyDel - > delete the specified key (multiple keys are allowed)
del key [key ...]Example:
1127.0.0.1:6379> set name liziba 2OK 3127.0.0.1:6379> get name 4"liziba" 5127.0.0.1:6379> set name liziba001 6OK 7127.0.0.1:6379> get name 8"liziba001" 9127.0.0.1:6379> del name 10(integer) 1 11127.0.0.1:6379> get name 12(nil)
2.2 batch key value pairs
The biggest advantage of batch key value reading and writing is to save network transmission overhead
Mset - > batch insert
mset key value [key value ...]Mget - > batch get
mget key [key ...]Example:
1127.0.0.1:6379> mset name1 liziba1 name2 liziba2 name3 liziba3 2OK 3127.0.0.1:6379> mget name1 name2 name3 41) "liziba1" 52) "liziba2" 63) "liziba3"
2.3 expiration set command
Expiration set is a mechanism by setting the expiration time of a cache key to automatically delete the cache after expiration.
Mode 1:
Example:
1127.0.0.1:6379> set name liziba 2OK 3127.0.0.1:6379> get name 4"liziba" 5127.0.0.1:6379> expire name 10 # After 10s, get name returns nil 6(integer) 1 7127.0.0.1:6379> get name 8(nil)
Mode 2:
setex key seconds valueExample:
1127.0.0.1:6379> setex name 10 liziba # After 10s, get name returns nil 2OK 3127.0.0.1:6379> get name 4(nil)
2.4 no creation or update
The above set operation does not exist. If it exists, it will be updated; At this time, if there is a scenario that does not need to be updated, you can use the following command
Setnx - > create does not exist update
Example:
1127.0.0.1:6379> get name 2(nil) 3127.0.0.1:6379> setnx name liziba 4(integer) 1 5127.0.0.1:6379> get name 6"liziba" 7127.0.0.1:6379> setnx name liziba_98 # Setting value again already exists, failed 8(integer) 0 9127.0.0.1:6379> get name 10"liziba"
2.5 counting
String (string) can also be used to count. If value is an integer, it can be self incremented. The range of auto increment must be within the interval access of signed long [- 92233720368547758089223372036854775808]
Incr - > auto increment 1
incr keyExample:
1127.0.0.1:6379> set fans 1000 2OK 3127.0.0.1:6379> incr fans # Self increment 1 4(integer) 1001
Incrby - > user defined cumulative value
incrby key increment1127.0.0.1:6379> set fans 1000 2OK 3127.0.0.1:6379> incr fans 4(integer) 1001 5127.0.0.1:6379> incrby fans 999 6(integer) 2000
Test the self increasing interval where value is an integer
Maximum:
1127.0.0.1:6379> set fans 9223372036854775808 2OK 3127.0.0.1:6379> incr fans 4(error) ERR value is not an integer or out of range
Minimum:
1127.0.0.1:6379> set money -9223372036854775808 2OK 3127.0.0.1:6379> incrby money -1 4(error) ERR increment or decrement would overflow
3, list
1. List related introduction
1.1 internal structure of list
Redis's list is equivalent to the LinkedList in the Java language. It is a two-way linked list data structure (but this structure is cleverly designed, which will be described later) and supports sequential traversal. Linked list structure has fast insertion and deletion operation, time complexity O(1), slow query, time complexity O(n).
1.2 usage scenario of list
According to the characteristics of Redis bidirectional list, it is also used for asynchronous queue. In the actual development, the task structures that need to be delayed are sequenced into strings and placed in the Redis queue. Another thread obtains data from this list for subsequent processing. The process is similar to the following figure:
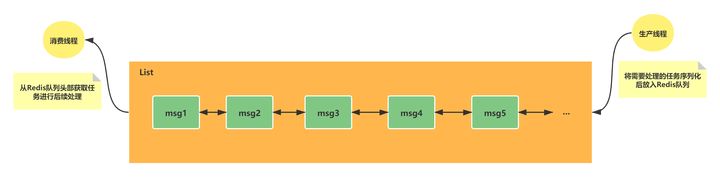
2. List instruction
2.1 right in left out - queue
Queue structure is a first in first out (FIFO) data structure (such as the order of queuing and ticket purchase). It is often used for similar functions of message queue, such as message queuing, asynchronous processing and so on. It ensures the access order of elements.
Lpush - > add element from left
Rpush - > add element from right
rpush key value [value ...]Llen - > get the length of the list
llen keyLpop - > pop up element from left
lpop key1127.0.0.1:6379> rpush code java c python # Add an element to the list 2(integer) 3 3127.0.0.1:6379> llen code # Get list length 4(integer) 3 5127.0.0.1:6379> lpop code # Pop up the first added element 6"java" 7127.0.0.1:6379> lpop code 8"c" 9127.0.0.1:6379> lpop code 10"python" 11127.0.0.1:6379> llen code 12(integer) 0 13127.0.0.1:6379> lpop code 14(nil)
2.2 right in right out - stack
The stack is a data structure of first in and last out (FILO) (for example, when the cartridge is pressed into the cartridge, the order in which the cartridge is fired is the stack). This data structure is generally used for reverse order output.
Lpush - > add element from left
lpush key value [value ...]Rpush - > add element from right
rpush key value [value ...]Rpop - > pop up elements from the right
rpop code1127.0.0.1:6379> rpush code java c python 2(integer) 3 3127.0.0.1:6379> rpop code # Pop up the last added element 4"python" 5127.0.0.1:6379> rpop code 6"c" 7127.0.0.1:6379> rpop code 8"java" 9127.0.0.1:6379> rpop code 10(nil)
2.3 slow operation
List is a linked list data structure. Its traversal is slow, so the performance related to traversal will increase with the increase of traversal range. Note that the index of the list runs as a negative number, - 1 represents the penultimate, and - 2 represents the penultimate. The same is true for others.
Lindex - > traversal to get the value at the specified index of the list
Lrange - > get all values from index start to stop
lrange key start stopLtrim - > intercept all values from index start to stop, and others will be deleted
ltrim key start stop1127.0.0.1:6379> rpush code java c python 2(integer) 3 3127.0.0.1:6379> lindex code 0 # Get data with index 0 4"java" 5127.0.0.1:6379> lindex code 1 # Get data with index 1 6"c" 7127.0.0.1:6379> lindex code 2 # Get data with index 2 8"python" 9127.0.0.1:6379> lrange code 0 -1 # Get all 0 to the penultimate data = = get all data 101) "java" 112) "c" 123) "python" 13127.0.0.1:6379> ltrim code 0 -1 # Intercept and factoring data from 0 to - 1 = = factoring all 14OK 15127.0.0.1:6379> lrange code 0 -1 161) "java" 172) "c" 183) "python" 19127.0.0.1:6379> ltrim code 1 -1 # Intercepted and factoring data from 1 to - 1 = = removed data with index 0 20OK 21127.0.0.1:6379> lrange code 0 -1 221) "c" 232) "python"
3. List (list) in-depth understanding
Redis's underlying storage list (list) is not a simple LinkedList, but a quicklist - "quick list". What is quicklist? It will be briefly introduced below. I am still learning the specific source code. We will discuss it later.
quicklist is a two-way list composed of multiple ziplists (compressed list); And what is this zip list? ziplist refers to a continuous memory storage space. When the number of elements is small, it will use a continuous memory space to store the list at the bottom of Redis. This can reduce the memory consumption caused by adding prev and next pointers to each element. The most important thing is to reduce the problem of memory fragmentation.
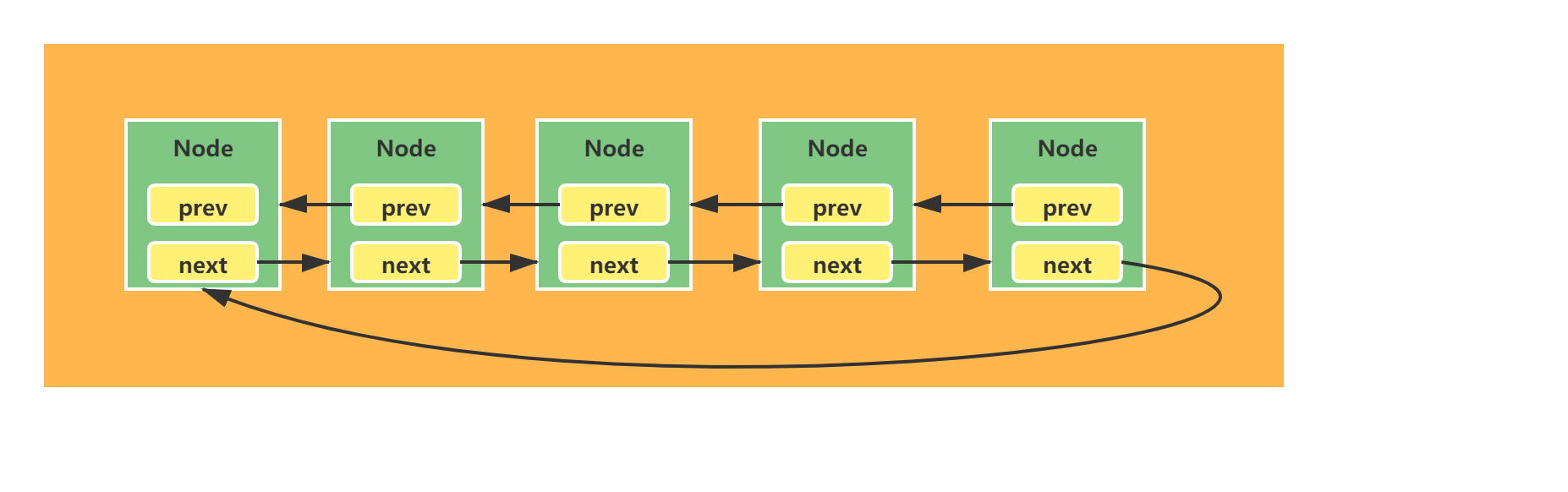
3.1 schematic diagram of common linked list structure
Each node node element will hold a pointer (Reference) of prev - > to execute the previous node node and next - > to the next node node. Although this structure supports sequential traversal, it also brings a lot of memory overhead. If the node node is only an int value, it can be imagined that the referenced memory proportion will be greater.
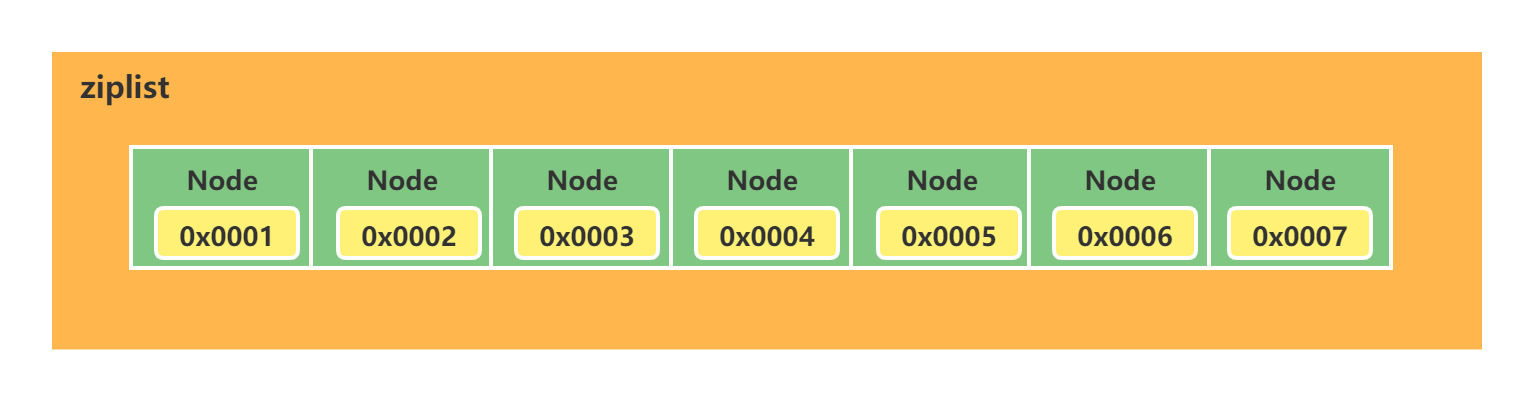
3.2 schematic diagram of ziplost
ziplist is a continuous memory address. There is no need to hold prev and next pointers between them. It can be accessed through address sequential addressing.
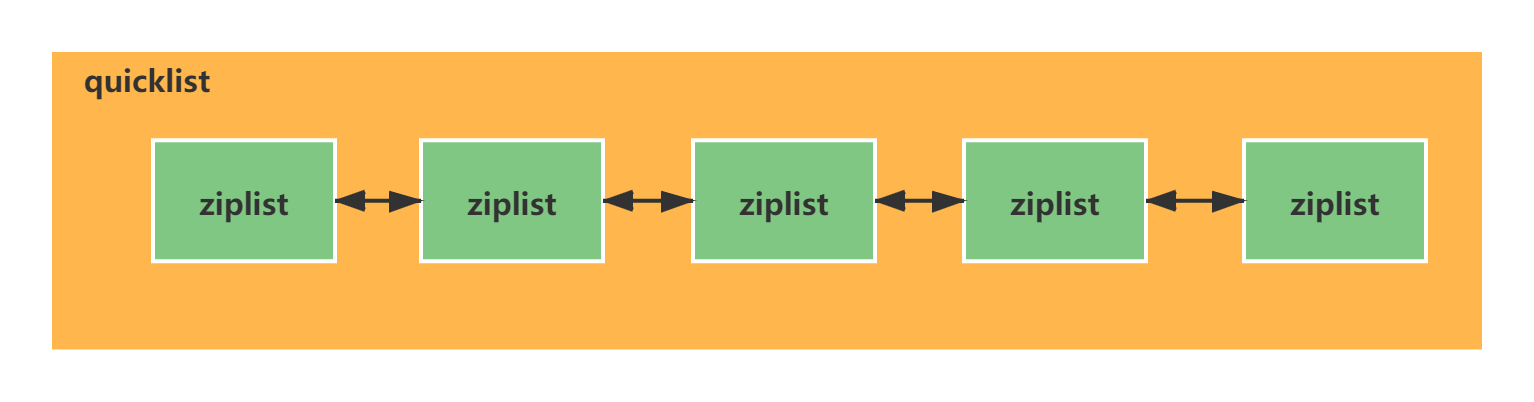
3.3 schematic diagram of QuickList
quicklist is a two-way linked list composed of multiple zip lists.
4, hash (Dictionary)
1. Introduction to hash (Dictionary)
1.1 internal structure of hash (Dictionary)
The hash (Dictionary) of Redis is equivalent to the HashMap in the Java language. It is an unordered dictionary distributed according to the hash value, and the internal elements are stored through key value pairs.
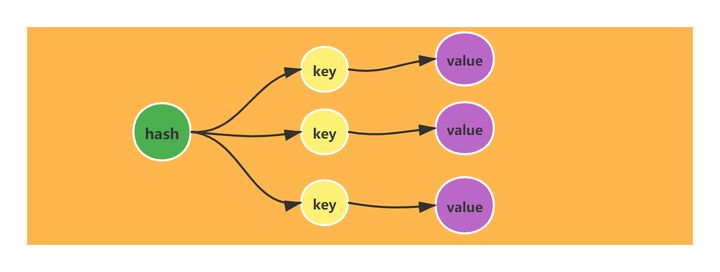
The implementation of hash (Dictionary) is also consistent with the structure of HashMap (JDK1.7) in Java. Its data structure is also a two-dimensional structure composed of array + linked list. The node elements are scattered on the array. If hash collision occurs, the linked list is connected in series on the array node.
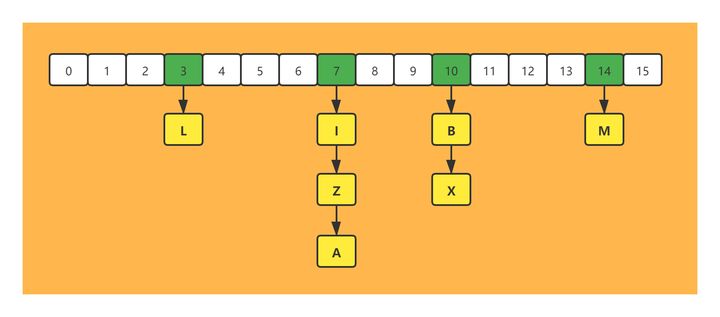
1.2 hash (Dictionary) expansion
The value stored in the hash (Dictionary) in Redis can only be a string value. In addition, the capacity expansion is also different from the HashMap in Java. HashMap in Java is completed at one time during capacity expansion. Considering that its core access is a single thread performance problem, Redis adopts a progressive rehash strategy in order to pursue high performance.
Progressive rehash means that it is not completed at one time, but multiple times. Therefore, it is necessary to take care of the old hash structure. Therefore, there will be old and new hash structures in the hash (Dictionary) in Redis. After rehash is completed, that is, after all the values of the old hash are moved to the new hash, the new hash will completely replace the previous hash in function.
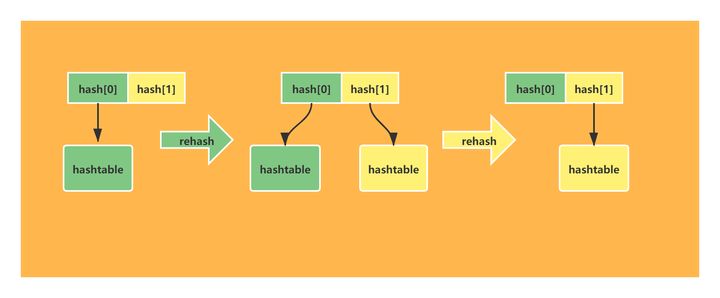
1.3 relevant usage scenarios of hash (Dictionary)
A hash (Dictionary) can be used to store information about an object. A hash (Dictionary) represents an object, a key of the hash represents an attribute of the object, and the value of the key represents the value of the attribute. Compared with string, hash (Dictionary) structure does not need to serialize the whole object for storage. In this way, partial acquisition can be performed during acquisition. In contrast, hash (Dictionary) has the following advantages and disadvantages:
- Read can be partially read to save network traffic
- The storage consumption is higher than that of a single string
2. Hash related instructions
2.1 hash (Dictionary) common instructions
Hset - > hash (Dictionary) inserts a value. If the dictionary does not exist, create a key to represent the dictionary name. field is equivalent to key, and value is the value of key
hset key field valueHmset - > batch setting
hmset key field value [field value ...]Example:
17.0.0.1:6379> hset book java "Thinking in Java" # "The string contains spaces. A" "" "package is required." 2(integer) 1 3127.0.0.1:6379> hset book python "Python code" 4(integer) 1 5127.0.0.1:6379> hset book c "The best of c" 6(integer) 1 7127.0.0.1:6379> hmset book go "concurrency in go" mysql "high-performance MySQL" # Batch setting 8OK
Hget - > get the value of the specified key in the dictionary
hget key fieldHgetall - > get all the key s and value s in the dictionary, and wrap the output
hgetall keyExample:
1127.0.0.1:6379> hget book java 2"Thinking in Java" 3127.0.0.1:6379> hgetall book 41) "java" 52) "Thinking in Java" 63) "python" 74) "Python code" 85) "c" 96) "The best of c"
HLEN - > get the number of key s of the specified dictionary
hlen keygive an example:
1127.0.0.1:6379> hlen book 2(integer) 5
2.2 tips for using hash (Dictionary)
In string (string), incr and incrby can be used to add the string whose value is an integer. In hash (Dictionary) structure, if a single sub key is an integer, it can also be added.
Hincrby - > Add: automatically add the integer value of a key in the hash (Dictionary)
hincrby key field increment1127.0.0.1:6379> hset liziba money 10 2(integer) 1 3127.0.0.1:6379> hincrby liziba money -1 4(integer) 9 5127.0.0.1:6379> hget liziba money 6"9"
Note that if it is not an integer, an error will be reported.
1127.0.0.1:6379> hset liziba money 10.1 2(integer) 1 3127.0.0.1:6379> hincrby liziba money 1 4(error) ERR hash value is not an integer
5, set
1. Introduction to set
1.1 internal structure of set
Redis's set is equivalent to the HashSet in the Java language. Its internal key value pairs are unordered and unique. It internally implements a special dictionary where all values are null.
After the last element in the collection is removed, the data structure is automatically deleted and memory is reclaimed.
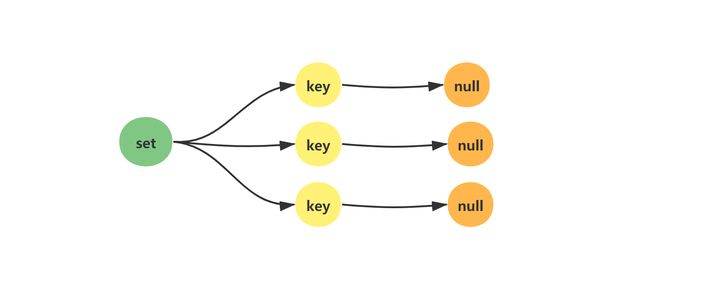
1.2 usage scenario of set
Due to its special de duplication function, set can be used to store the ID of the winning user in the activity, so as to ensure that a user will not win twice.
2. Set related instructions
Sadd - > add collection member, key value, collection name, member value, collection element, element cannot be duplicate
sadd key member [member ...]1127.0.0.1:6379> sadd name zhangsan 2(integer) 1 3127.0.0.1:6379> sadd name zhangsan # Cannot be repeated. 0 will be returned if repeated 4(integer) 0 5127.0.0.1:6379> sadd name lisi wangwu liumazi # Support adding multiple elements at a time 6(integer) 3
Smembers - > view all the elements in the collection. Note that they are out of order
smembers key1127.0.0.1:6379> smembers name # Output all elements in the collection out of order 21) "lisi" 32) "wangwu" 43) "liumazi" 54) "zhangsan"
Sismember - > query whether the collection contains an element
sismember key member1127.0.0.1:6379> sismember name lisi # Include return 1 2(integer) 1 3127.0.0.1:6379> sismember name tianqi # Return 0 without 4(integer) 0
Scard - > get the length of the collection
scard key1127.0.0.1:6379> scard name 2(integer) 4
Spop - > pop-up elements. count refers to the number of pop-up elements
spop key [count]1127.0.0.1:6379> spop name # The default pop-up is one 2"wangwu" 3127.0.0.1:6379> spop name 3 41) "lisi" 52) "zhangsan" 63) "liumazi"
6, zset (ordered set)
1. Introduction to Zset (ordered set)
1.1 internal structure of Zset (ordered set)
Zset (ordered set) is the most frequently asked data structure in Redis. It is similar to the combination of SortedSet and HashMap in the Java language. On the one hand, it ensures the uniqueness of the internal value value through set, and on the other hand, it sorts through the score (weight) of value. The sorting function is realized through Skip List.
After the last element value of Zset (ordered set) is removed, the data structure is automatically deleted and the memory is recycled.
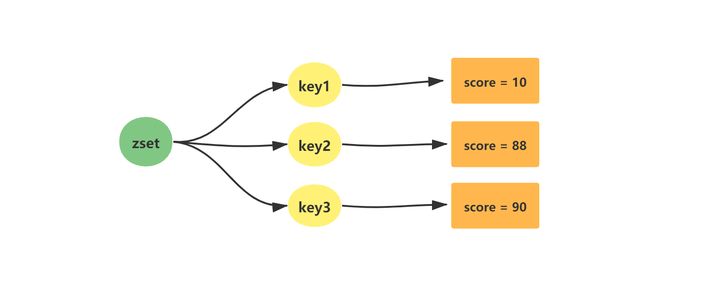
1.2 relevant usage scenarios of Zset (ordered set)
Using zset's de duplication and ordering effects can be used in many usage scenarios, for example:
- Store the list of fans. value is the ID of fans and score is the time stamp of attention, so you can sort the attention of fans
- Store the student's score, value makes the student's ID and score is the student's score, so that the student's score can be ranked
2. Zset (ordered set) related instructions
1. Zadd - > add an element to the set. If the set does not exist, create a new one. key represents the name of the zset set, score represents the weight of the element, and member represents the element
zadd key [NX|XX] [CH] [INCR] score member [score member ...]1127.0.0.1:6379> zadd name 10 zhangsan 2(integer) 1 3127.0.0.1:6379> zadd name 10.1 lisi 4(integer) 1 5127.0.0.1:6379> zadd name 9.9 wangwu 6(integer) 1
2. Zrange - > sort the elements in the output set from small to large according to the score weight. If the weight is the same, sort them according to the dictionary order of value ([lexical order])
Out of range subscripts do not cause errors. For example, when the value of start is larger than the maximum subscript of the ordered set, or start > stop, the zrange command simply returns an empty list. On the other hand, if the value of the stop parameter is greater than the maximum subscript of the ordered set, Redis treats stop as the maximum subscript.
You can use the with scores option to return the member together with its score value. The returned list is expressed in the format of value1,score1,..., valuen and score n. Client libraries may return more complex data types, such as arrays, tuples, and so on.
zrange key start stop [WITHSCORES]1127.0.0.1:6379> zrange name 0 -1 # Get all elements and output them in ascending order of score 21) "wangwu" 32) "zhangsan" 43) "lisi" 5127.0.0.1:6379> zrange name 0 1 # Get the elements of the first and second slot s 61) "wangwu" 72) "zhangsan" 8127.0.0.1:6379> zadd name 10 tianqi # Add an element with a score of 10 based on the above 9(integer) 1 10127.0.0.1:6379> zrange name 0 2 # If the key s are equal, the output is sorted according to the value dictionary 111) "wangwu" 122) "tianqi" 133) "zhangsan" 14127.0.0.1:6379> zrange name 0 -1 WITHSCORES # With scores output weights 151) "wangwu" 162) "9.9000000000000004" 173) "tianqi" 184) "10" 195) "zhangsan" 206) "10" 217) "lisi" 228) "10.1"
3. Zrevrange - > the elements in the output set are weighted from large to small according to score. If the weights are the same, they are sorted in reverse order according to the dictionary of value
The positions of members are arranged in descending order (from large to small) according to the score value. Members with the same score value are arranged in reverse lexical order. Except that the members are arranged in descending order of the score value, other aspects of the ZREVRANGE command are the same as the zrange key start stop [with scores] command
zrevrange key start stop [WITHSCORES]1127.0.0.1:6379> zrevrange name 0 -1 WITHSCORES 21) "lisi" 32) "10.1" 43) "zhangsan" 54) "10" 65) "tianqi" 76) "10" 87) "wangwu" 98) "9.9000000000000004"
4. Zcard - > when the key exists and is an ordered set type, the cardinality of the ordered set is returned. When the key does not exist, 0 is returned
zcard key1127.0.0.1:6379> zcard name 2(integer) 4
5. Zscore - > returns the score value of the member in the ordered set key. If the member element is not a member of the ordered set key or the key does not exist, nil is returned
zscore key member z1127.0.0.1:6379> zscore name zhangsan 2"10" 3127.0.0.1:6379> zscore name liziba 4(nil)
6. Zrank - > returns the ranking of members in the ordered set key. The ordered set members are arranged in the order of increasing score value (from small to large).
The ranking is based on 0, that is, the member with the lowest score is ranked as 0
zrank key member1127.0.0.1:6379> zrange name 0 -1 21) "wangwu" 32) "tianqi" 43) "zhangsan" 54) "lisi" 6127.0.0.1:6379> zrank name wangwu 7(integer) 0
7. Zrangebyscore - > returns all members in the ordered set key whose score value is between min and max (including those equal to min or max). Ordered set members are arranged in the order of increasing score value (from small to large).
min and max can be - inf and + inf, so you can use commands like [ZRANGEBYSCORE] without knowing the lowest and highest score values of the ordered set.
By default, the value of the interval is closed. You can also use the optional [open interval] less than or greater than by adding (symbol) before the parameter
zrangebyscore key min max [WITHSCORES] [LIMIT offset count]1127.0.0.1:6379> zrange name 0 -1 WITHSCORES # Output all elements 21) "wangwu" 32) "9.9000000000000004" 43) "tianqi" 54) "10" 65) "zhangsan" 76) "10" 87) "lisi" 98) "10.1" 10127.0.0.1:6379> zrangebyscore name 9 10 111) "wangwu" 122) "tianqi" 133) "zhangsan" 14127.0.0.1:6379> zrangebyscore name 9 10 WITHSCORES # Output score 151) "wangwu" 162) "9.9000000000000004" 173) "tianqi" 184) "10" 195) "zhangsan" 206) "10" 21127.0.0.1:6379> zrangebyscore name -inf 10 # -inf starts at negative infinity 221) "wangwu" 232) "tianqi" 243) "zhangsan" 25127.0.0.1:6379> zrangebyscore name -inf +inf # +inf until positive infinity 261) "wangwu" 272) "tianqi" 283) "zhangsan" 294) "lisi" 30127.0.0.1:6379> zrangebyscore name (10 11 # 10 < score <=11 311) "lisi" 32127.0.0.1:6379> zrangebyscore name (10 (10.1 # 10 < socre < -11 33(empty list or set) 34127.0.0.1:6379> zrangebyscore name (10 (11 351) "lisi"
8. Zrem - > remove one or more members from the ordered set key. Nonexistent members will be ignored
zrem key member [member ...]1127.0.0.1:6379> zrange name 0 -1 21) "wangwu" 32) "tianqi" 43) "zhangsan" 54) "lisi" 6127.0.0.1:6379> zrem name zhangsan # Removing Elements 7(integer) 1 8127.0.0.1:6379> zrange name 0 -1 91) "wangwu" 102) "tianqi" 113) "lisi"
7, Skip List
1. Introduction
The full name of a jump table is called a jump table, or jump table for short. Jump table is a randomized data structure, which is essentially an ordered linked list that can be used for binary search. Jump table adds multi-level index to the original ordered linked list to realize fast search through index. Skip table can not only improve the search performance, but also improve the performance of insert and delete operations.
Skip list, a random data structure, can be regarded as a variant of binary tree. Its performance is very similar to that of red black tree and AVL tree; However, the implementation of skip list is much simpler than the first two. At present, the zset implementation of Redis adopts skip list (other LevelDB also use skip list).
Simple comparison between RBT red black tree and skip list:
RBT red black tree
- Insertion and query time complexity O(logn)
- Natural order of data
- Realize complex, design discoloration, left-hand and right-hand balance and other operations
- Need to lock
Skip List skip list
- Insertion and query time complexity O(logn)
- Natural order of data
- Simple implementation, linked list structure
- No locking required
2. Analysis of Skip List algorithm
2.1 Skip List papers
The paper of Skip List is posted here. Please see the paper for detailed research. Some formulas, codes and pictures below come from the paper.
Skip Lists: A Probabilistic Alternative to Balanced Trees
2.2 Skip List dynamic diagram
First, understand the process of inserting node elements in Skip List through a dynamic diagram, which is from Wikipedia.
2.3 performance analysis of skip list algorithm
2.3.1 algorithm for calculating random layers
The first analysis is the process of calculating random numbers when performing the insertion operation. This process will involve the calculation of layers, so it is very important. The node has the following characteristics:
- Each node has a pointer to the first level
- If the node has layer i pointer, the probability of layer i+1 is p
- The node has the maximum number of layers, MaxLevel
Pseudo code for calculating the number of random layers:
Examples in the paper
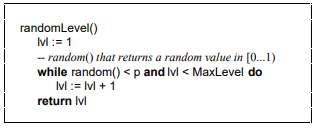
Java version
1public int randomLevel(){
2 int level = 1;
3 // random() returns a random number of [0... 1]
4 while (random() < p && level < MaxLevel){
5 level += 1;
6 }
7 return level;
8}The code contains two variables P and MaxLevel. In Redis, the values of these two parameters are:
1p = 1/4 2MaxLevel = 64
2.3.2 average number of pointers contained in a node
Skip List is a space for time data structure. The space here refers to the number of pointers contained in each node. This part is the additional internal memory overhead, which can be used to measure the space complexity. random() is a random number, so the higher the number of node layers, the lower the probability (the promotion rate data in Redis standard source code is 1 / 4. Relatively speaking, the structure of Skip List is relatively flat and the layer height is relatively low). Its quantitative analysis is as follows:
- level = 1 probability is 1-p
- The probability of level > = 2 is p
- level = 2 probability p(1-p)
- Level > = 3 probability is p^2
- level = 3 probability p^2(1-p)
- The probability of level > = 4 is p^3
- level = 4 probability p^3(1-p)
- ......
Get the average number of layers of the node (the average number of pointers contained in the node):
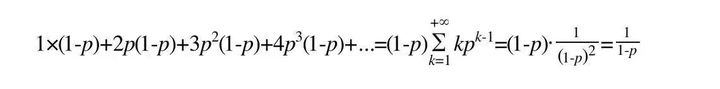
Therefore, the average number of pointers calculated by p=1/4 in Redis is 1.33
2.3.3 time complexity calculation
The following calculation comes from the content of the paper
Assuming p=1/2, in the skip list of 16 elements generated with p=1/2, we may happen to have 9 elements, 1-level 3 elements, 3-level 3 elements and 1-level 14 elements (this is unlikely, but it may happen) . how should we deal with this situation? If we use the standard algorithm and start our search at level 14, we will do a lot of useless work. Then where should we start the search? At this time, we assume that there are n elements in the SkipList, and the expectation of the number of elements at level L is 1/p; the probability of each element appearing at level L is p^(L-1) , then the expectation of the number of elements at level L is n * (p^L-1); get 1/p = n * (p^L-1)
11 / p = n * (p^L-1) 2n = (1/p)^L 3L = log(1/p)^n
So we should choose MaxLevel = log(1/p)^n
Definition: MaxLevel = L(n) = log(1/p)^n
To calculate the time complexity of Skip List, you can use reverse thinking to trace the time complexity by starting from node x with layer i and returning to the starting point. There are two situations at node X:
- If there is a (i+1) layer pointer in node x, the probability of climbing up one level is p, corresponding to the following figure situation c
- If there is no (i+1) layer pointer in node x, then climb one level to the left with a probability of 1-p, corresponding to the following figure situation b
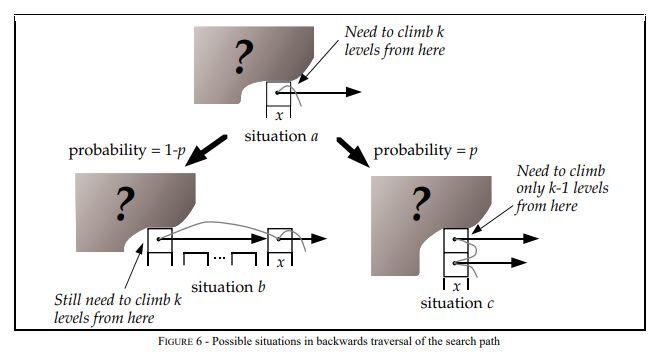
Let C(k) = the expected cost (i.e. length) of the search path climbing up K level s in the infinite list, then the deduction is as follows:
1C(0)=0 2C(k)=(1-p)×(situation b Find length of) + p×(situation c Find length of) 3C(k)=(1-p)(C(k)+1) + p(C(k-1)+1) 4C(k)=1/p+C(k-1) 5C(k)=k/p
According to the above deduction results, the expected length of climbing k levels is k/p, and the length of climbing a level is 1/p.
Since MaxLevel = L(n), C(k) = k / p, the expected value is: (L(n) – 1) / p; substituting L(n) = log(1/p)^n can obtain: (log(1/p)^n - 1) / p; substituting p = 1 / 2 can obtain: 2 * log2^n - 2, that is, the time complexity of O(logn).
3. Skip List feature and its implementation
2.1 Skip List feature
Skip List skip list usually has the following features
- The Skip List contains multiple layers. Each layer is called a level, and the level increases from 0
- The Skip List 0 layer, that is, the bottom layer, should contain all elements
- Each level / layer is an ordered list
- A layer with a small level contains elements of a layer with a large level, that is, element a appears in layer X, so all levels / layers with X > z > = 0 should contain element a
- Each node element consists of a node key, a node value, and an array of pointers to the level of the current node
2.2 Skip List query
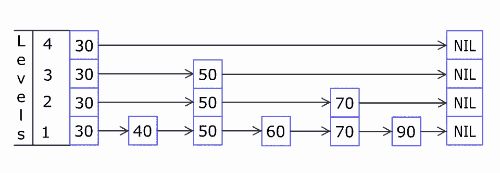
Assuming that these elements already exist in the initial Skip List jump list, their distribution structure is as follows:
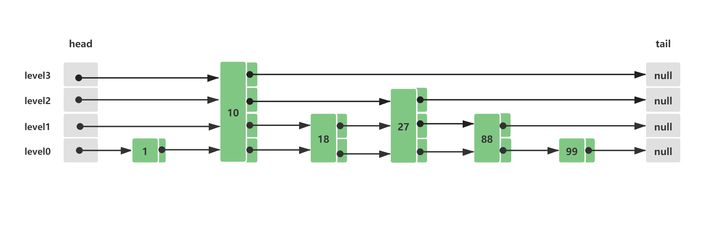
At this time, query node 88, and its query route is as follows:
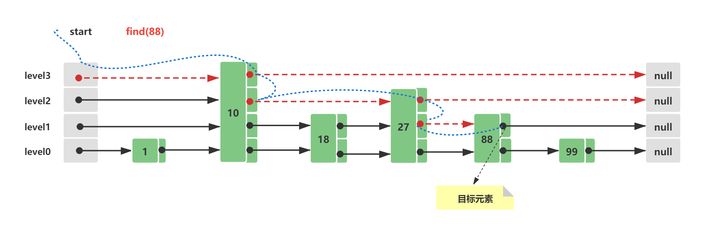
- Starting from the top level 3 of the Skip List jump list, it is found that 10 < 88 & & the value of subsequent nodes is null & & there is a lower level 2
- Level 2 10 traverses backward, 27 < 88 & & the value of subsequent nodes is null & & there is lower level 1
- Level 1 27 traverses backward, 88 = 88, query hit
2.3 Skip List insertion
The initial structure of Skip List is consistent with that in 2.3. At this time, assuming that the value of the inserted new node element is 90, the insertion route is as follows:
- Query the insertion position, which is the same as the Skip List query method. Here, the first node larger than 90 needs to be queried. It is inserted in front of this node, 88 < 90 < 100
- Construct a new node Node(90) and calculate a random level for the inserted node Node(90). Here, it is assumed that the calculation is 1. This level is randomly calculated. It may be 1, 2, 3, 4... And the larger the level, the smaller the possibility. It mainly depends on the random factor X. the probability of the number of layers is roughly calculated as (1/x)^level. If the level is greater than the current maximum level 3, head and tail nodes need to be added
- After the node is constructed, it needs to be inserted into the list. The insertion is a very simple step - > node (88). Next = node (90); Node(90).prev = Node(80); Node(90).next = Node(100); Node(100).prev = Node(90);
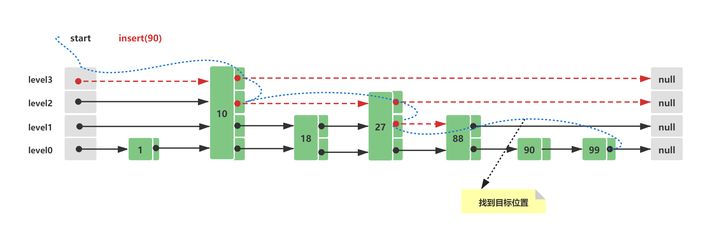
2.4 Skip List deletion
The process of deleting is to query the nodes, then delete them, and then combine the left and right nodes of the deleted nodes in the form of linked list. There is no drawing here
4. Handwritten implementation of a simple Skip List
It is relatively simple to implement a Skip List, which is mainly divided into two steps:
- The nodes defining the Skip List are stored in the form of linked lists. Therefore, the nodes hold pointers to adjacent nodes, where prev and next are pointers to the front and rear nodes of the same level, and down and up are pointers to the upper and lower nodes of multiple levels of the same Node
- Defines the implementation class of Skip List, including the insertion, deletion and query of nodes. The query operations are divided into ascending query and descending query (backward and forward query). The elements between the default nodes of Skip List implemented here are ascending linked list
3.1 defining Node
The Node class mainly includes the following important attributes:
- Score - > node weight, which is the same as the score in Redis. It is used to sort node elements
- Value - > the real data stored in the node. Only String type data can be stored
- Prev - > the predecessor node of the current node, the same level
- Next - > the successor node of the current node, the same level
- Down - > lower level node of the current node, different levels of the same node
- Up - > upper level node of the current node, different levels of the same node
1package com.liziba.skiplist;
2
3/**
4 * <p>
5 * Skip table node element
6 * </p>
7 *
8 * @Author: Liziba
9 * @Date: 2021/7/5 21:01
10 */
11public class Node {
12
13 /** The score value of the node is sorted according to the score value */
14 public Double score;
15 /** Real data stored by nodes */
16 public String value;
17 /** The reference of the front, rear, lower and upper nodes of the current node */
18 public Node prev, next, down, up;
19
20 public Node(Double score) {
21 this.score = score;
22 prev = next = down = up = null;
23 }
24
25 public Node(Double score, String value) {
26 this.score = score;
27 this.value = value;
28 }
29}3.2 operation class of skiplist node element
SkipList mainly includes the following important attributes:
- The uppermost header node of the header node in head - > skiplist (the header node of the layer with the largest level). This node does not store elements. It is used to make the query starting position when building lists and queries. For the specific structure, see the structure in 2.3
- The top level tail node of the tail node in tail - > skiplist (the tail node of the layer with the largest level). This node does not store elements and is the termination flag for querying a level
- Level - > total layers
- Size - > number of node elements in skip list
- Random - > is used to randomly calculate node levels. If random. Nextdouble() < 1 / 2, the level of the current node needs to be increased. If the level increased by the current node exceeds the total level, the head and tail (total level) need to be increased
1package com.liziba.skiplist;
2
3import java.util.Random;
4
5/**
6 * <p>
7 * Skip table implementation
8 * </p>
9 *
10 * @Author: Liziba
11 */
12public class SkipList {
13
14 /** Topmost header node */
15 public Node head;
16 /** Topmost tail node */
17 public Node tail;
18 /** Total layers */
19 public int level;
20 /** Number of elements */
21 public int size;
22 public Random random;
23
24 public SkipList() {
25 level = size = 0;
26 head = new Node(null);
27 tail = new Node(null);
28 head.next = tail;
29 tail.prev = head;
30 }
31
32 /**
33 * Query the precursor node location of the inserted node
34 *
35 * @param score
36 * @return
37 */
38 public Node fidePervNode(Double score) {
39 Node p = head;
40 for(;;) {
41 // The current level traverses backward and compares the score. If it is less than the current value, it traverses backward
42 while (p.next.value == null && p.prev.score <= score)
43 p = p.next;
44 // Traverse the next level of the rightmost node
45 if (p.down != null)
46 p = p.down;
47 else
48 break;
49 }
50 return p;
51 }
52
53 /**
54 * Insert the node in front of the fidePervNode(Double score)
55 *
56 * @param score
57 * @param value
58 */
59 public void insert(Double score, String value) {
60
61 // Front node of current node
62 Node preNode = fidePervNode(score);
63 // Current newly inserted node
64 Node curNode = new Node(score, value);
65 // If both scores and values are equal, return directly
66 if (curNode.value != null && preNode.value != null && preNode.value.equals(curNode.value)
67 && curNode.score.equals(preNode.score)) {
68 return;
69 }
70
71 preNode.next = curNode;
72 preNode.next.prev = curNode;
73 curNode.next = preNode.next;
74 curNode.prev = preNode;
75
76 int curLevel = 0;
77 while (random.nextDouble() < 1/2) {
78 // If the level of the inserted node is greater than or equal to the level, a new level will be added
79 if (curLevel >= level) {
80 Node newHead = new Node(null);
81 Node newTail = new Node(null);
82 newHead.next = newTail;
83 newHead.down = head;
84 newTail.prev = newHead;
85 newTail.down = tail;
86 head.up = newHead;
87 tail.up = newTail;
88 // Change the head and tail node pointers to new ones to ensure that the head and tail pointers are always the top-level head and tail nodes
89 head = newHead;
90 tail = newTail;
91 ++level;
92 }
93
94 while (preNode.up == null)
95 preNode = preNode.prev;
96
97 preNode = preNode.up;
98
99 Node copy = new Node(null);
100 copy.prev = preNode;
101 copy.next = preNode.next;
102 preNode.next.prev = copy;
103 preNode.next = copy;
104 copy.down = curNode;
105 curNode.up = copy;
106 curNode = copy;
107
108 ++curLevel;
109 }
110 ++size;
111 }
112
113 /**
114 * Query the node element of the specified score
115 * @param score
116 * @return
117 */
118 public Node search(double score) {
119 Node p = head;
120 for (;;) {
121 while (p.next.score != null && p.next.score <= score)
122 p = p.next;
123 if (p.down != null)
124 p = p.down;
125 else // Traverse to the bottom
126 if (p.score.equals(score))
127 return p;
128 return null;
129 }
130 }
131
132 /**
133 * Output the elements in the Skip List in ascending order (stored in ascending order by default, so traverse from the list head to tail)
134 */
135 public void dumpAllAsc() {
136 Node p = head;
137 while (p.down != null) {
138 p = p.down;
139 }
140 while (p.next.score != null) {
141 System.out.println(p.next.score + "-->" + p.next.value);
142 p = p.next;
143 }
144 }
145
146 /**
147 * Outputs the elements in the Skip List in descending order
148 */
149 public void dumpAllDesc() {
150 Node p = tail;
151 while (p.down != null) {
152 p = p.down;
153 }
154 while (p.prev.score != null) {
155 System.out.println(p.prev.score + "-->" + p.prev.value);
156 p = p.prev;
157 }
158 }
159
160
161 /**
162 * Delete node elements in Skip List
163 * @param score
164 */
165 public void delete(Double score) {
166 Node p = search(score);
167 while (p != null) {
168 p.prev.next = p.next;
169 p.next.prev = p.prev;
170 p = p.up;
171 }
172 }
173}
Click focus to learn about Huawei cloud's new technologies for the first time~