Topic source

Click me to enter the ACwing official website to submit

Title Description

Put an 8 × The chessboard of 8 is divided as follows: cut off a rectangular chessboard from the original chessboard and make the rest also rectangular, and then continue to divide the rest. After cutting (n − 1) times, there are n rectangular chessboards together with the last remaining rectangular chessboard. (each cutting can only be carried out along the edge of the chessboard grid)

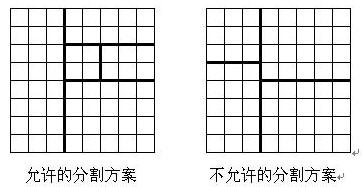
Each grid on the original chessboard has a score, and the total score of a rectangular chessboard is the sum of the scores of each grid.

Now we need to divide the chessboard into n rectangular chessboards according to the above rules, and minimize the mean square deviation of the total score of each rectangular chessboard.

Mean square deviation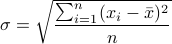
, where average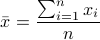
， x i x_i xi is the second i i The total score of i rectangular chessboard.

Please program the given chessboard and n to find the minimum value of mean square deviation.

Input format
The first line is an integer n.

From line 2 to line 9, there are 8 non negative integers less than 100 in each line, indicating the score of the corresponding grid on the chessboard. Two adjacent numbers in each line are separated by a space.

Output format
Output the minimum mean square difference (rounded to three decimal places).

Data range
1<n<15
Input sample:
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
Output example:
1.633

Topic idea

• General idea of the topic

The goal is to divide the chessboard into n blocks. For each cut, only one chessboard can be selected for operation. Given the value in the block, the minimum total variance is calculated.

• Analysis question type

The data range is not too large. Seek the maximum value and try to use DP.
According to the form, it can be divided into two sides, with the meaning of divide and conquer. Try to use the thinking mode of interval DP to solve the problem.

• Analysis of dynamic transfer equation

Determine the nature of DP set. Because it is partitioned and does not interfere with each other, the first four dimensions represent the coordinates of the upper left corner and the lower right corner, because it can only be tangent n − 1 n-1 n − 1 times, there is a limit on the number of times, so you have to add one dimension to record the number of times. The value represented is the total square difference of the region. (the average is the total number / n. after entering, you will know the average value, which can be solved directly according to the variance formula, using the interval prefix and)
There are two cutting methods after a given chessboard, one is cross cutting and the other is vertical cutting. After cutting, which part must be selected for the next operation.

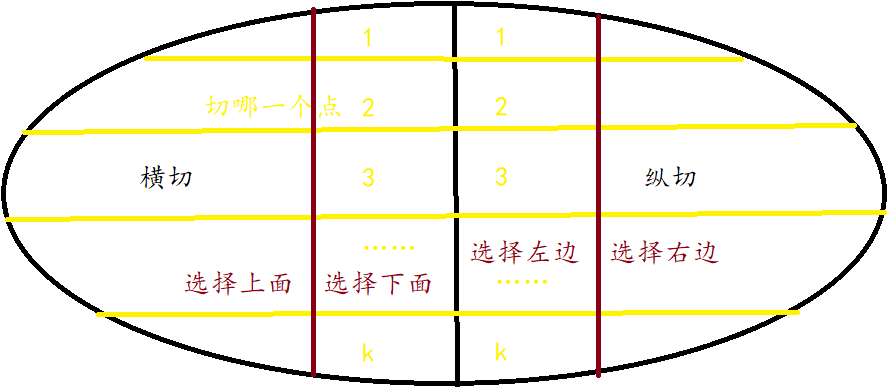
This diagram is simple and clear, showing all the States.

It's a bit like divide and conquer, so write DP recursively.

Dynamic programming equation, please see the code~

AC code

#include<bits/stdc++.h> 
using namespace std;

#define _for(i, a, b) for (int i = (a); i < (b); ++i) 
#define _rep(i, a, b) for (int i = (a); i <= (b); ++i)
#define For(i, a, b) for (int i = (a); i >= (b); --i)
#define debug(a) cout << #a << " = " << a << ENDL
#define ENDL "\n"
#define x first 
#define y second 
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;

const int N = 15 + 5, M = 8 + 5, INF = 0x3f3f3f3f;
int m = 8, n;
double X, s[M][M], f[M][M][M][M][N];

double Get(int x1, int y1, int x2, int y2) {
	double sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] - X;
	return sum * sum / n;
}

double dp(int x1, int y1, int x2, int y2, int k) {
	double& v = f[x1][y1][x2][y2][k];
	if (v >= 0) return v;
	if (k == 1) return v = Get(x1, y1, x2, y2);

	v = INF;
	_rep(i, y1, y2) {
		v = min(v, Get(x1, y1, x2, i) + dp(x1, i + 1, x2, y2, k - 1));
		v = min(v, dp(x1, y1, x2, i, k - 1) + Get(x1, i + 1, x2, y2));
	}

	_rep(i, x1, x2) {
		v = min(v, Get(x1, y1, i, y2) + dp(i + 1, y1, x2, y2, k - 1));
		v = min(v, dp(x1, y1, i, y2, k - 1) + Get(i + 1, y1, x2, y2));
	}
	return v;
}

int main() {
#ifdef LOCAL
	freopen("data.in", "r", stdin);
#endif 
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n;
	_rep(i, 1, m) _rep(j, 1, m) {
		cin >> s[i][j];
		s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
	}
	X = s[m][m] / n;
	
	memset(f, -1, sizeof f);
	printf("%0.3lf\n", sqrt(dp(1, 1, m, m, n)));
	return 0;
} 

reflect

This topic has been done once, so I didn't take it seriously, resulting in a waste of time!!
We must pay attention to the first step of the problem!!!!