Python WeChat Subscription Applet Course Video

https://edu.csdn.net/course/detail/36074

Python Actual Quantitative Transaction Finance System

https://edu.csdn.net/course/detail/35475
By ChesiumBy Chesium\text{By}\ \mathsf{Chesium}

The DPLL algorithm, fully known as the Davis-Putnam-Logemann-Loveland (Davis-Putnam-Logemann-Loveland) algorithm, is a complete, backtracking-based search algorithm for determining the satisfiability of propositional logic formulas (in the form of a conjunctive paradigm), that is, an algorithm (or a class) for solving the SAT (Boolean satisfiability problem).

Introduction to SAT issues

What is the Boolean satisfiability problem? Given a true value expression that contains logical variables (also known as variables, propositional variables, atoms, expressed in lowercase letters a,b,... a,b,... a,b,\dots), logical and (AND, denoted as \wedge), logical or (OR, denoted as \vee), and non (NOT, negative, denoted as \neg) operators, such as:

(a∧¬b∧(¬(c∨d∨¬a)∨(b∧¬d)))∨(¬(¬(¬b∨a)∧c)∧d)(a∧¬b∧(¬(c∨d∨¬a)∨(b∧¬d)))∨(¬(¬(¬b∨a)∧c)∧d)(a\wedge\neg b\wedge(\neg(c\vee d\vee\neg a)\vee(b\wedge\neg d)))\vee(\neg(\neg(\neg b\vee a)\wedge c)\wedge d)
Is there a set of assignments to these variables (such as assigning all aaa and ddd to TrueTrue\mathrm{True}, assigning all bbb and ccc to FalseFalse\mathrm{False}), which results in the final operation of the whole formula as TrueTrue\mathrm{True}? If possible, this property is called satisfiability of this logical formula. How to quickly and efficiently judge the satisfiability of any specified logical formula is an important problem in theoretical computer science, and is also the first problem proved to be NP-complete (NPC).

Violence Programs

It's easy to think about a way to determine "violence": test each possible arrangement of the assignments to these variables (for example, assign them all to TrueTrue\mathrm{True}, one to TrueTrue\mathrm{True}, the other to FalseFalsemathrm{False}...), and if there is an assignment arrangement that makes the result of the formula TrueTrue\mathrm{True}, Then you can see that this formula is satisfiable. However, it is clear that in the worst case this method requires us to test 2n2n2^n assignment permutations (n n n is the number of variables), and it is also not negligible to check the final result of each assignment permutation. Therefore, as the size of the formula increases, the computational complexity required for this violent algorithm increases exponentially, which is unacceptable to us.

Overview of algorithms

However, according to the existing computational complexity theory, the SAT problem can not be solved within the polynomial time complexity, and DPLL algorithm is no exception.

DPLL algorithm is a kind of search algorithm, which is very similar to DFS (Depth-first search), or DPLL algorithm itself belongs to the category of DFS, which is similar to the "violence" algorithm we envisioned above: search all possible assignment permutations.

Specifically, the algorithm will select a variable in the formula (proposition variable), assign it to TrueTrue\mathrm{True}, simplify the assigned formula, if the simplified formula is satisfied (recursively judged), then the original formula is also satisfied. Otherwise, assign the variable to FalseFalse\mathrm{False} in turn, and make a recursive decision that cannot be satisfied, then the original formula is unsatisfactory.

This is called the splitting rule because it separates the original problem into two simpler problems.

Conceptual Description

The DPLL algorithm solves the Conjunctive normal form (CNF), which is a logical formula with the following form:

(a∨b∨¬c)∧(¬d∨x1∨¬x2∨⋯∨x7)∧(¬r∨v∨g)∧⋯∧(a∨d∨¬d)(a∨b∨¬c)∧(¬d∨x1∨¬x2∨⋯∨x7)∧(¬r∨v∨g)∧⋯∧(a∨d∨¬d)(a\vee b\vee\neg c)\wedge
(\neg d\vee x_1\vee\neg x_2\vee\dots\vee x_7)\wedge
(\neg r\vee v\vee g)\wedge\dots\wedge
(a\vee d\vee\neg d)
It consists of several brackets enclosing part of the logic and composition, each of which is the logic or composition of many variables or variables'negative (logical non). It can be proved that all logical formulas that contain only logical AND, logical OR, logical NOT, logical implication and parentheses can be transformed into equivalent and proper norms. Next, we call the whole paradigm a "formula". We call each bracketed part a clause of the formula, and each variable in each clause or its negation a literal.

You can see that for the whole formula to result in TrueTrue\mathrm{True}, all its clauses must be TrueTrue\mathrm{True}, that is, at least one text in each clause is TrueTrue\mathrm{True}, which is used below.

The simplification step in the DPLL algorithm is essentially to remove all clauses that have a value of TrueTrue\mathrm{True} after assignment and all text that has a value of FalseFalse\mathrm{False} after assignment.

Simplification steps

These two simplification steps are the main difference between DPLL algorithm and our "violence" algorithm. They greatly reduce the amount of search, that is, they speed up the algorithm.

First simplification step: Unit propagation

We call a clause a unit clause that contains only one (unassigned) variable. According to the above conclusion, to make the formula TrueTrue\mathrm{True}, this clause must be TrueTruemathrm{True}, that is, the text corresponding to this variable must be assigned TrueTruemathrm{True}.

For example, the following formula:

(a∨b∨c∨¬d)∧(¬a∨c)∧(¬c∨d)∧(a)(a∨b∨c∨¬d)∧(¬a∨c)∧(¬c∨d)∧(a)(a\vee b\vee c\vee\neg d)\wedge(\neg a\vee c)\wedge(\neg c\vee d)\wedge(a)
The last clause is the unit clause, that is, we want the text (a)(a)(a) to be TrueTrue\mathrm{True}.

Next, we will deal with the occurrence of this variable in other clauses in turn, if one of the words in the other clause is the same as the words in the unit clause, as in the example above (a_b_c_d)(a_b_c_d)(a_vee b\vee c\vee\neg d) clause, we know that the value of (a) (a) must be True8744;mathrm{True}, and So this clause must also be TrueTrue\mathrm{True}, which means that this clause does not impose additional constraints on the entire formula (that is, the values of b, c, D b, c, d do not affect the value of this clause). We can completely ignore this clause, so delete it.

Consider the second clause in the above formula, where the negative text (a)(a)(a) appears. We know that it can't be TrueTrue\mathrm{True}. To have this clause have a value of TrueTruemathrm{True}, we can only trust the value of ccc. We can delete a\neg a completely because it does not affect the value of the clause.

The third clause in the first clause does not contain the occurrence of (a)(a)(a) or its negation, that is, the value of a a a does not affect the value of this clause, we can just leave it unchanged.

In this way, the above formulas are simplified to:

©∧(¬c∨d)∧(a)©∧(¬c∨d)∧(a)©\wedge(\neg c\vee d)\wedge(a)
This operation is called unit clause propagation.

Summary: For all clauses that contain only one text LL\mathrm{L}, for each clause in the remainder of the formula CC\mathrm{C}:

• If CC\mathrm{C} contains LL\mathrm{L} (non-negative), delete CC\mathrm{C}.
• If CCmathrm{C} contains L_Lnegmathrm{L}, delete this LLnegmathrm{L}.

After one operation, we found a new unit clause in the formula ©©© ， We can continue to propagate the unit clause once until no variable corresponding to any unit clause appears in other clauses in the whole formula.

The above formula can be reduced to:

©∧(d)∧(a)©∧(d)∧(a)©\wedge(d)\wedge(a)
Now even though each clause in the formula is a unit clause, its corresponding variables c, d, a c, d, a c, d, a do not appear in Clauses other than the unit clause. Unit clause propagation is no longer useful. We need to implement the second simplification step.

Second simplification step: Pure literal elimination

If a variable only appears once in the entire formula, we can assign it appropriately so that its clause is TrueTrue\mathrm{True}. Specifically, if the occurrence was negative, then assign the variable to FalseFalse\mathrm{False}, which makes the corresponding text TrueTrue\mathrm{True}, even if the clause it is in is TrueTrue\mathrm{True}, or assign the variable to TrueTrue\mathrm{True}, which ultimately makes the clause it is in TrueTruemathrm{True}. Next, it is treated the same way as when the clause is TrueTrue\mathrm{True} in the propagation of the above unit clause - delete the clause.

To summarize a sentence, delete the clause in which all isolated variables are located.

For the following formulas:

(¬r∨u)∧(r∨c∨¬u)∧(¬k∨r)∧(¬d∧k)(¬r∨u)∧(r∨c∨¬u)∧(¬k∨r)∧(¬d∧k)(\neg r\vee u)\wedge(r\vee \color{red}{c}\vee\neg u)\wedge(\neg k\vee r)\wedge(\color{blue}{\neg d}\wedge k)
The red variable C C C appears only once in the whole formula, and we can assign it TrueTruemathrm{True} so that the clause it is in (r_c_u)(r_c_u)(r\vee \color{red}{c}\veeneg u) is TrueTruemathrm{True}, and we can delete it. Similarly, the blue-marked variable ddd appears only once in the whole formula and is negative. We can assign it to FalseFalse\mathrm{False}, make its clause TrueTruemathrm{True}, or delete it. Thus, the formula is simplified to:

(¬r∨u)∧(¬k∨r)(¬r∨u)∧(¬k∨r)(\neg r\vee u)\wedge(\neg k\vee r)
Take another look at the example above:

©∧(d)∧(a)©∧(d)∧(a)©\wedge(d)\wedge(a)
All three variables appear in isolation. We can delete all three clauses and the whole formula will be empty, so we can judge that the original formula is satisfactory.

These are the two simplification steps.

Algorithm flow

The pseudocode for the DPLL algorithm is given below. As mentioned earlier, the DPLL algorithm is essentially a depth-first search algorithm, so they are very similar.

1Algorithm  DPLL(CNF  Φ):=2do  UP(Φ)  until  It changed nothing.3do  PLE(Φ)  until  It changed nothing.4if  Φ=∅  then5return  true.6if  ∃L∈Φ,L=∅  then7return  false.8x←ChooseVariable(Φ)9return  DPLL(Φx→true)  or  DPLL(Φx→false)1Algorithm  DPLL(CNF  Φ):=2do  UP(Φ)  until  It changed nothing.3do  PLE(Φ)  until  It changed nothing.4if  Φ=∅  then5return  true.6if  ∃L∈Φ,L=∅  then7return  false.8x←ChooseVariable(Φ)9return  DPLL(Φx→true)  or  DPLL(Φx→false)\begin{aligned}
&\mathtt{1}\quad
\mathtt{\color{red}{Algorithm}}\ \ \mathrm{DPLL}(\mathtt{CNF}\ \ \color{green}{\Phi}):=\
&\mathtt{2}\quad\qquad
\mathtt{\color{red}{do}}\ \ \text{UP}(\color{green}{\Phi})\ \
\mathtt{\color{red}{until}}\ \ \text{It changed nothing}.\
&\mathtt{3}\quad\qquad
\mathtt{\color{red}{do}}\ \ \text{PLE}(\color{green}{\Phi})\ \
\mathtt{\color{red}{until}}\ \ \text{It changed nothing}.\
&\mathtt{4}\quad\qquad
\mathtt{\color{red}{if}}\ \ \color{green}{\Phi}=\varnothing\ \ \mathtt{\color{red}{then}}\
&\mathtt{5}\quad\qquad\qquad
\mathtt{\color{red}{return}}\ \ \mathrm{\color{blue}{true}}.\
&\mathtt{6}\quad\qquad
\mathtt{\color{red}{if}}\ \ \exists L\in\color{green}{\Phi},L=\varnothing\ \ \mathtt{\color{red}{then}}\
&\mathtt{7}\quad\qquad\qquad
\mathtt{\color{red}{return}}\ \ \mathrm{\color{blue}{false}}.\
&\mathtt{8}\quad\qquad
x\leftarrow\mathrm{ChooseVariable}(\color{green}{\Phi})\
&\mathtt{9}\quad\qquad
\mathtt{\color{red}{return}}\ \ \mathrm{DPLL}(\color{green}{\Phi}_{x\to\mathrm{\color{blue}{true}}})
\ \ \mathtt{\color{red}{or}}\ \ \mathrm{DPLL}(\color{green}{\Phi}_{x\to\mathrm{\color{blue}{false}}})
\end{aligned}
Where UP( Φ) UP( Φ)\ mathrm{UP}(\Phi) and PLE ( Φ) PLE( Φ)\ mathrm{PLE}(\Phi) refers to the pair of formulas, respectively ΦΦ\ Phi propagates unit clauses and eliminates isolated text, ChooseVariable. Φ) ChooseVariable( Φ)\ mathrm{ChooseVariable}(\Phi) refers to the formula ΦΦ\ Selecting a variable in Phi (unassigned) can greatly affect the efficiency of DPLL algorithm according to the existing research. Depending on the strategy of variable selection, there are many variants of DPLL algorithm, but this is not in the scope of our discussion now. As a beginner, we will let ChooseVariable (heuristic function) Φ) ChooseVariable( Φ)\ mathrm{ChooseVariable}(\Phi) directly selects the first variable in the variable sequence.

In line 999 Φ X_true Φ X_truePhi_ {x\to\mathrm{true}} means that the formula will be ΦΦ\ The variable xxx in Phi is assigned to TrueTrue\mathrm{True}, and the formula after assigning the variable (deleting the clause containing its affirmative occurrence and deleting the text in its negative form) is handled according to the way described in the simplification rule. Φ X_false Φ X_falsePhi_ The same is true for {x\to\mathrm{false}}, except that the two operations are reversed.

You can see that this is a recursive program, and the original formula is not empty for the input Φ 0 Φ 0\Phi_0, which aborts in two cases:

• formula ΦΦ\ Phi is empty, which can only be caused by the fact that each clause must be TrueTrue\mathrm{True} after being assigned to a variable, which is incorrect ΦΦ\ Assignments to other variables in Phi result in constraints and are all deleted. This means that the original Φ 0 Φ 0\Phi_0 After assignment of a part (and possibly all) of the variable, the value of all its clauses is set to TrueTrue\mathrm{True}. Φ 0 Φ 0\Phi_0 is satisfied.
• formula ΦΦ\ Phi contains an empty clause, which can only be caused by the fact that all text in this clause is assigned a value of FalseFalse\mathrm{False} and therefore deleted, then it is impossible for this clause to be TrueTrue\mathrm{True}, the formula ΦΦ\ Phi is unsatisfactory. (This does not mean Φ 0 Φ 0\Phi_0 cannot be satisfied because this is only a possible assignment arrangement)

Specific implementation

Next, we're starting to implement a foundation from scratch (without the complex ChooseVariable). Φ) ChooseVariable( Φ)\ DPLL L algorithm for mathrm{ChooseVariable}(\Phi) heuristic).

Notice that the algorithm involves a large number of text deletion and clause deletion operations, and may appear anywhere in the middle of the text list and clause list (that is, not simply deleting the head or end), as well as more traversal in processing individual clauses and text without random access. I use a Linked list to store the formulas we work with. Specifically, we use a two-dimensional chain table to store the conjugation paradigm, which can be viewed as a list of clauses, and each clause as a list of writing.

Each text has two attributes: the variable number (integer) and whether it is a negative text (Boolean value). When entering, we discretize all variable identifiers into variable numbers.

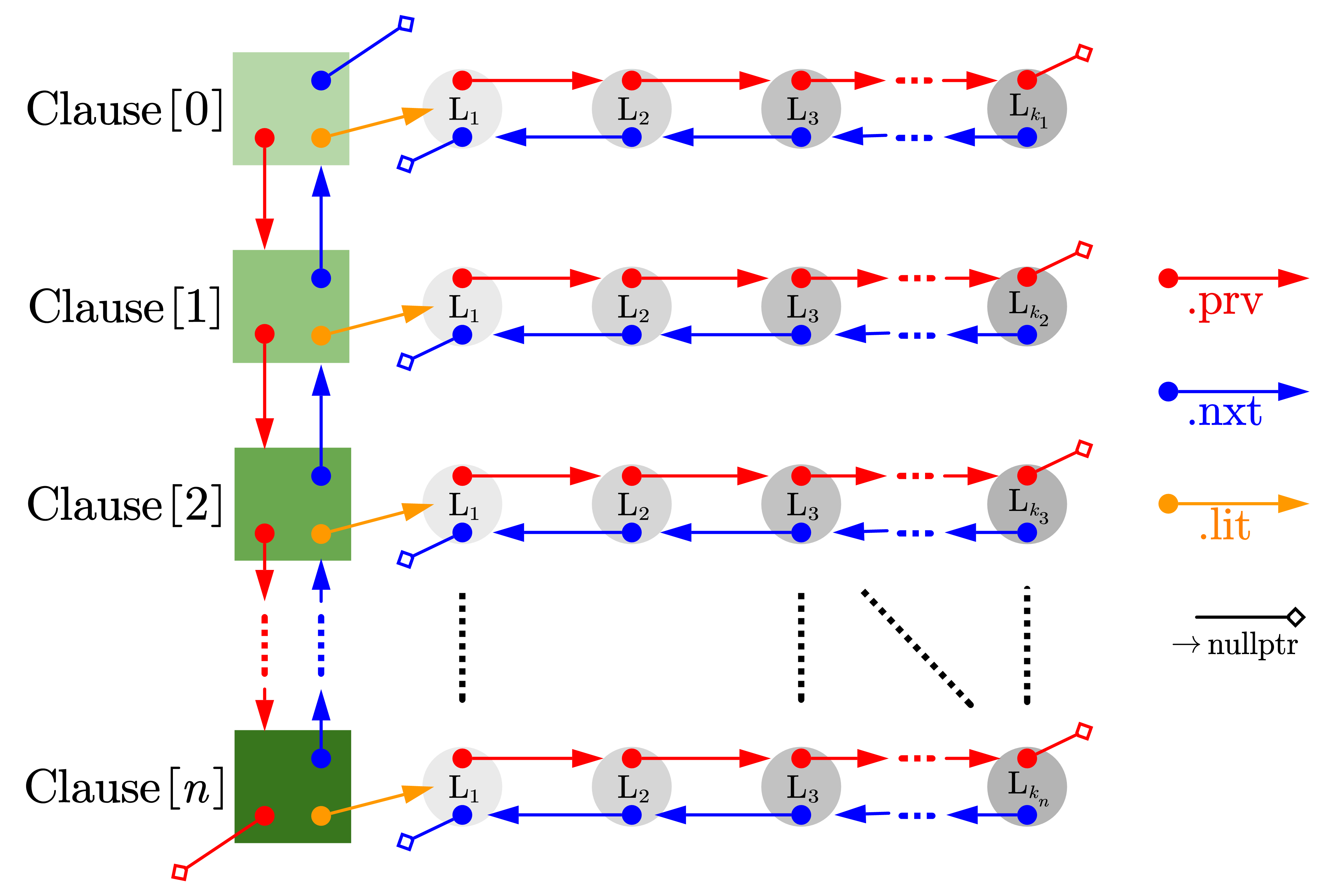
Figure 1: Storing the join paradigm using a two-dimensional chain table
To delete a text, we only need to delete the previous text. Nxt. The nxt\mathrm{.nxt} pointer points to the next text and places the next text's. Prv. The prv\mathrm{.prv} pointer points to the previous text, and deleting the clause is the same.

However, we find that the algorithm involves finding all the words of a particular logical variable. If a variable is assigned a value, all its words must be processed in turn. If only the structure of the chain list above is adopted, all clauses and words must be traversed in each process. We can efficiently traverse all the text of any variable by maintaining another two-dimensional chain table indexed by its name. It looks like adding a lot of jumpers to the list structure above. For the conjunction paradigm:

(a∨¬c∨d)∧(d∨¬b∨c∨¬t)∧(¬a∨b∨c)(a∨¬c∨d)∧(d∨¬b∨c∨¬t)∧(¬a∨b∨c)(a\vee\neg c\vee d)\wedge(d\vee\neg b\vee c\vee\neg t)\wedge(\neg a\vee b\vee c)
We can then build a structure to store the following:

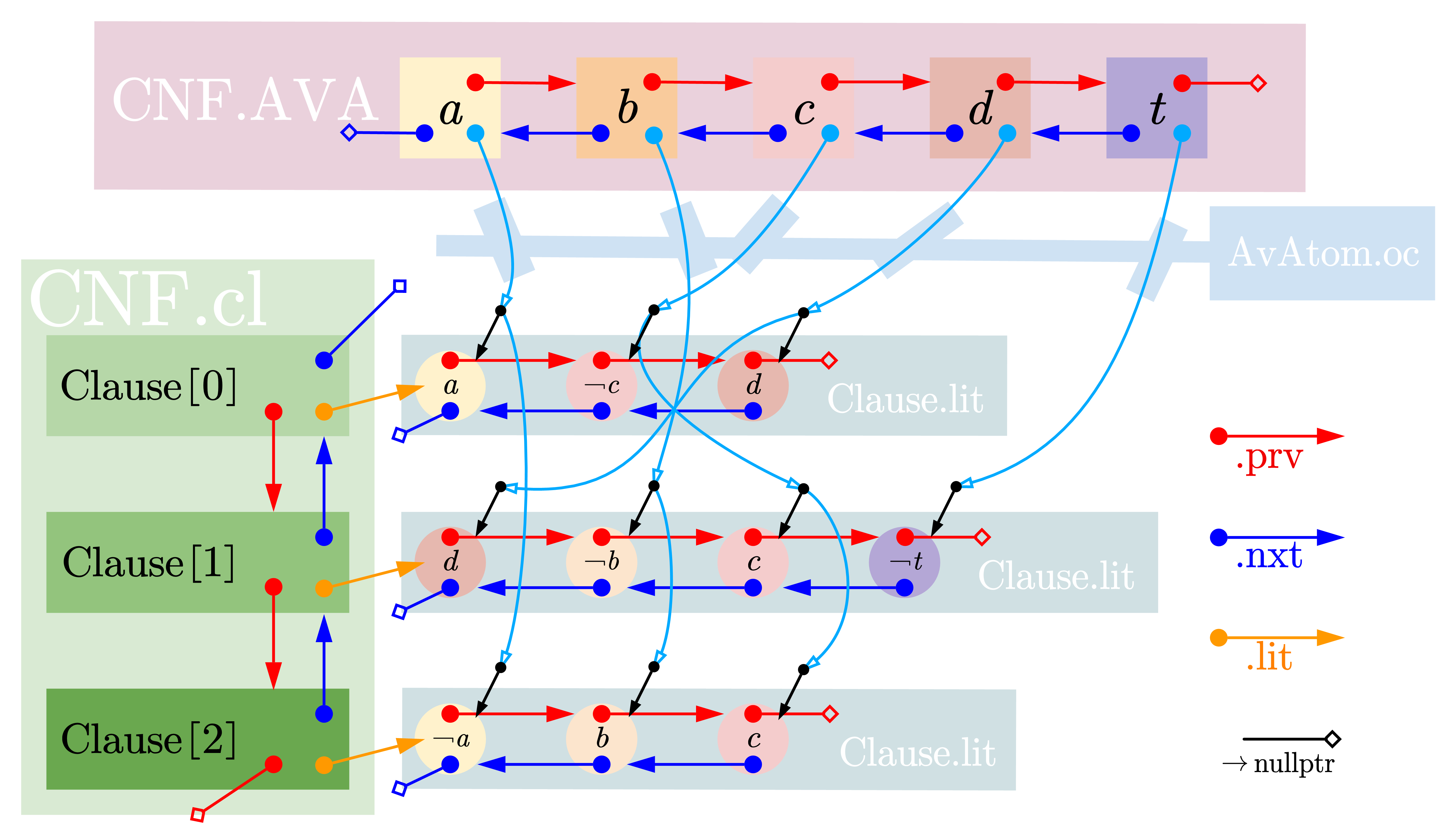
Figure 2: Adding a jumper to a two-dimensional chain table for more efficient traversal
Of course, only part of the key pointer structure is drawn, and the mid-sky blue "jumper" is also bidirectional. We can also find clauses by text and their corresponding text lists by adding some additional pointer storage.

In addition to the structure in the diagram, by maintaining a set (or list) of "unit clauses that are not propagated by unit clauses" in the deletion of text and clauses, and a set of variables with only one corresponding text, we can find all the unit clauses and isolated variables without traversing.

However, the challenge lies ahead: this is a recursive algorithm that involves backtracking previous historical versions. Specifically, formulas cannot be satisfied under a certain combination of assignments, so we need to restore the simplification and assignment operations we just performed and check that the formulas can be satisfied under different assignments, that is, enter another search branch.

How do I go back? The simplest example is in pseudocode, where a historical version of the entire formula structure is copied directly by calling a copy of the parameters in the function during recursion. This sounds inefficient but easy to implement, but in fact, for a data structure with so many pointers, copying a complete, independent copy necessarily involves a lot of pointer redirection. This is very difficult and involves a lot of detail. Moreover, even if it is implemented, with a large number of recursive layers, the program will consume a lot of memory and contain a lot of redundant duplicates.

Here, I use a data structure based on stack and incremental storage. The DPLL algorithm can be seen as an algorithm for DFS searching on a binary tree. When the program executes this recursive algorithm, it maintains a stack in the call to a function (which is itself recursively) to store local variables in each function call. I've copied this structure by using stacks to store the parts of the formula structure that change in the assignments of one-tier searches.

Specifically, each arrow in Figure 2 above is a "pointer stack" that stores a series of pointers that identify a series of changes in the pointer's recursion process. In the process of simplifying and assigning each found formula state node, we only visit and modify the pointer at the top of the stack, and use a set to identify the pointer stack that has been modified in this process (simplification and assignment), which is maintained by a stack. Traversing the set at the top of the stack, releasing the top of all the pointer stacks, restores the version of the historical formula. The above data structure can be viewed as a simple partially persistent list group, but there are also many areas for optimization.

Implementation Code

Some of the core code is given below, and the complete code is visible:

• Chesium/DPLL (github.com)

https://github.com/Chesium/DPLL

See the end of the article for instructions on how to use the code.

Pointer Stack Chain List implementation:

|  | template  |
|  | struct node { |
|  | stack *> prvPS, nxtPS; |
|  |  slist *L; |
|  |  T *X = nullptr; |
|  |  |
|  |  node(slist *l, T *x = nullptr, node *\_prv = nullptr, |
|  |  node *\_nxt = nullptr) { |
|  |  this->L = l; |
|  | if (x != nullptr) this->X = new T(*x); |
|  |  this->init\_upd(\_prv, \_nxt); |
|  |  } |
|  |  |
|  | void \_\_upd(node *\_prv, node *\_nxt) { |
|  | if (\_prv != nullptr) this->prvPS.push(\_prv); |
|  | if (\_nxt != nullptr) this->nxtPS.push(\_nxt); |
|  |  } |
|  |  |
|  | void init\_upd(node *\_prv, node *\_nxt) { |
|  | if (\_prv != nullptr) |
|  | while (!this->prvPS.empty()) this->prvPS.pop(); |
|  | if (\_nxt != nullptr) |
|  | while (!this->nxtPS.empty()) this->nxtPS.pop(); |
|  |  this->\_\_upd(\_prv, \_nxt); |
|  |  } |
|  |  |
|  | void upd(node *\_prv, node *\_nxt) { |
|  | if (\_prv != nullptr) { |
|  | auto it = this->L->Recorder->ch.top().find(&(this->prvPS)); |
|  | if (it == this->L->Recorder->ch.top().end()) |
|  |  this->L->Recorder->ch.top().insert(&(this->prvPS)); |
|  | else |
|  |  this->prvPS.pop(); |
|  |  this->prvPS.push(\_prv); |
|  |  } |
|  | if (\_nxt != nullptr) { |
|  | auto it = this->L->Recorder->ch.top().find(&(this->nxtPS)); |
|  | if (it == this->L->Recorder->ch.top().end()) |
|  |  this->L->Recorder->ch.top().insert(&(this->nxtPS)); |
|  | else |
|  |  this->nxtPS.pop(); |
|  |  this->nxtPS.push(\_nxt); |
|  |  } |
|  |  } |
|  |  |
|  | bool isHead() { return this->L->begin() == this; } |
|  | bool isTail() { return this->L->end() == this; } |
|  |  node *prev() { return this->prvPS.top(); } |
|  |  node *next() { return this->nxtPS.top(); } |
|  | }; |
|  |  |
|  | template  |
|  | struct slist { |
|  | stack *> beginPS, endPS; |
|  |  rmRecorder *Recorder = nullptr; |
|  |  |
|  |  slist() { |
|  | auto primNode = new node(this); |
|  |  this->beginPS.push(primNode); |
|  |  this->endPS.push(primNode); |
|  |  } |
|  |  |
|  |  node *begin() { return this->beginPS.top(); } |
|  |  node *end() { return this->endPS.top(); } |
|  |  |
|  | void regRec(rmRecorder *rec) { this->Recorder = rec; } |
|  |  |
|  | bool empty() { return this->begin() == this->end(); } |
|  |  |
|  | bool single() { |
|  | if (this->empty()) return false; |
|  | return this->begin()->next() == this->end(); |
|  |  } |
|  |  |
|  | void add(T x) { |
|  | if (this->empty()) { |
|  | while (!this->beginPS.empty()) this->beginPS.pop(); |
|  |  this->beginPS.push(new node(this, &x, nullptr, this->end())); |
|  |  this->end()->init\_upd(this->begin(), nullptr); |
|  |  } else { |
|  | auto NewNode = new node(this, &x, this->end()->prev(), this->end()); |
|  |  this->end()->prev()->init\_upd(nullptr, NewNode); |
|  |  this->end()->init\_upd(NewNode, nullptr); |
|  |  } |
|  |  } |
|  |  |
|  | void rm(node *nd) { |
|  | if (nd->L != this) return; |
|  | if (nd == this->end()) return; |
|  | if (nd == this->begin()) { |
|  | auto it = this->Recorder->ch.top().find(&this->beginPS); |
|  | if (it == this->Recorder->ch.top().end()) |
|  |  this->Recorder->ch.top().insert(&this->beginPS); |
|  | else |
|  |  this->beginPS.pop(); |
|  |  this->beginPS.push(nd->next()); |
|  |  } else { |
|  |  nd->prev()->upd(nullptr, nd->next()); |
|  |  nd->next()->upd(nd->prev(), nullptr); |
|  |  } |
|  |  } |
|  |  |
|  |  T *front() { return this->begin()->X; } |
|  |  |
|  |  T *back() { return this->end()->prev()->X; } |
|  | }; |
|  |  |
|  | template  |
|  | struct rmRecorder { |
|  | stack<set<stack *> *>> ch; |
|  | int layer = 0; |
|  |  |
|  |  rmRecorder() { this->nextLayer(); } |
|  |  |
|  | void nextLayer() { |
|  |  this->ch.push(set<stack *> *>()); |
|  |  this->layer++; |
|  |  } |
|  |  |
|  | void backtrack() { |
|  | for (auto it = this->ch.top().begin(); it != this->ch.top().end(); it++) |
|  |  (*it)->pop(); |
|  |  this->layer--; |
|  |  ch.pop(); |
|  |  } |
|  | }; |

Data structure section:

|  | struct Literal { |
|  |  llu index; // |
|  | bool neg; |
|  |  CNF *cnf; |
|  |  node *cl; |
|  |  node *oc; |
|  |  Literal(CNF *\_cnf, string s, bool \_neg); |
|  | string str(); |
|  | void RemoveOccurrence(); |
|  | }; |
|  |  |
|  | struct Clause { |
|  |  slist *lt; |
|  |  CNF *cnf; |
|  |  Clause(CNF *\_cnf); |
|  | string str(); |
|  | }; |
|  |  |
|  | struct Occur { |
|  |  node *lit; |
|  |  Occur(node *\_lit) { this->lit = \_lit; } |
|  | }; |
|  |  |
|  | struct AvAtom { |
|  |  llu index; |
|  |  slist *oc; |
|  |  CNF *cnf; |
|  |  AvAtom(CNF *\_cnf, llu i); |
|  | }; |
|  |  |
|  | struct CNF { |
|  | map<string, llu> Dict; |
|  | vector<string> Atoms; |
|  | vector scheme; |
|  |  llu AtomN = 0; |
|  |  slist CL; |
|  |  slist AVA; |
|  | vector *> avAtoms; |
|  |  rmRecorder Rec\_Literal; |
|  |  rmRecorder Rec\_Clause; |
|  |  rmRecorder Rec\_Occur; |
|  |  rmRecorder Rec\_AvAtom; |
|  | stack<list> Rec\_assign; |
|  |  CNF() { |
|  |  this->CL.regRec(&this->Rec\_Clause); |
|  |  this->AVA.regRec(&this->Rec\_AvAtom); |
|  |  } |
|  | void read(); |
|  | string str(); |
|  | string occurStr(); |
|  | string schemeStr(); |
|  | void removeLiteral(node *cl, node *lit); |
|  | void removeClause(node *cl); |
|  |  ll AssignLiteralIn(node *cl, node *unit); |
|  | bool PureLiteralAssign(); |
|  | bool UnitPropagate(); |
|  | void nextLayer(); |
|  | void backtrack(); |
|  | bool containEmptyClause = false; |
|  | bool DPLL(bool disableSimp); |
|  | }; |
|  |  |
|  | void CNF::removeLiteral(node *cl, node *lit) { |
|  | cout << "DEL literal \"" << lit->X->str() << "\" in \"" << cl->X->str() |
|  |  << "\"" << endl; |
|  |  lit->X->RemoveOccurrence(); |
|  |  cl->X->lt->rm(lit); |
|  | } |
|  |  |
|  | void CNF::removeClause(node *cl) { |
|  | cout << "DEL Clause \"" << cl->X->str() << "\"" << endl; |
|  | for (auto lit = cl->X->lt->begin(); lit != cl->X->lt->end(); |
|  |  lit = lit->next()) |
|  |  lit->X->RemoveOccurrence(); |
|  |  this->CL.rm(cl); |
|  | } |
|  |  |
|  | void CNF::nextLayer() { |
|  |  this->Rec\_Literal.nextLayer(); |
|  |  this->Rec\_Clause.nextLayer(); |
|  |  this->Rec\_Occur.nextLayer(); |
|  |  this->Rec\_AvAtom.nextLayer(); |
|  |  this->Rec\_assign.push(list()); |
|  | } |
|  |  |
|  | void CNF::backtrack() { |
|  |  this->Rec\_Literal.backtrack(); |
|  |  this->Rec\_Clause.backtrack(); |
|  |  this->Rec\_Occur.backtrack(); |
|  |  this->Rec\_AvAtom.backtrack(); |
|  | for (auto it = this->Rec\_assign.top().begin(); |
|  |  it != this->Rec\_assign.top().end(); it++) |
|  |  this->scheme[*it] = 0; |
|  |  this->Rec\_assign.pop(); |
|  | } |

Algorithmic body:

|  | ll CNF::AssignLiteralIn(node *cl, node *unit) { |
|  | this->scheme[unit->X->index] = unit->X->neg ? 2 : 1; |
|  | this->Rec\_assign.top().push\_back(unit->X->index); |
|  | bool changed = false; |
|  | for (auto it = cl->X->lt->begin(); it != cl->X->lt->end(); it = it->next()) |
|  | if (it->X->index == unit->X->index) { |
|  | if (it->X->neg == unit->X->neg) { |
|  | this->removeClause(cl); |
|  | return 1; |
|  |  } else { |
|  | this->removeLiteral(cl, it); |
|  | if (cl->X->lt->empty()) { |
|  | this->containEmptyClause = true; |
|  | return 2; |
|  |  } |
|  |  changed = true; |
|  |  } |
|  |  } |
|  | return changed ? 1 : 0; |
|  | } |
|  |  |
|  | bool CNF::UnitPropagate() { |
|  | bool ok = false; |
|  | for (auto it1 = this->CL.begin(); it1 != this->CL.end(); it1 = it1->next()) |
|  | if (it1->X->lt->single()) { |
|  |  node *A = it1->X->lt->begin(); |
|  | for (auto it2 = this->CL.begin(); it2 != this->CL.end(); |
|  |  it2 = it2->next()) { |
|  | if (it1 == it2) continue; |
|  |  ll res = this->AssignLiteralIn(it2, A); |
|  | if (res == 2) return false; |
|  | if (res) ok = true; |
|  |  } |
|  | if (ok) return true; |
|  |  } |
|  | return false; |
|  | } |
|  |  |
|  | bool CNF::PureLiteralAssign() { |
|  | for (llu i = 0; i < this->AtomN; i++) |
|  | if (this->avAtoms[i]->X->oc->single()) { |
|  | this->scheme[this->avAtoms[i]->X->index] = |
|  | this->avAtoms[i]->X->oc->begin()->X->lit->X->neg ? 2 : 1; |
|  | this->Rec\_assign.top().push\_back(this->avAtoms[i]->X->index); |
|  | this->removeClause(this->avAtoms[i]->X->oc->begin()->X->lit->X->cl); |
|  | return true; |
|  |  } |
|  | return false; |
|  | } |
|  |  |
|  | bool CNF::DPLL(bool disableSimp = false) { |
|  |  stack STACK; |
|  |  AvAtom *x; |
|  |  ll layerNow = -1, Status; |
|  |  STACK.push(0); |
|  | while (!STACK.empty()) { |
|  |  Status = STACK.top(); |
|  |  STACK.pop(); |
|  | /***/ cout << "=== NEW STATUS : " << Status << " ===" << endl; |
|  | while (layerNow >= abs(Status)) { |
|  |  layerNow--; |
|  | /***/ cout << "BACKTRACK: -> " << layerNow << endl; |
|  | this->backtrack(); |
|  |  } |
|  |  layerNow = abs(Status); |
|  | /***/ cout << "FORMULA: begin processing(layer=" << layerNow |
|  |  << "):" << endl; |
|  | /***/ cout << this->str(); |
|  | this->nextLayer(); |
|  | if (Status == 0) { |
|  | /***/ cout << "INIT: skip assignments" << endl; |
|  | goto SIMPLIFICATION; |
|  |  } |
|  |  x = this->AVA.begin()->X; |
|  | /***/ cout << "ASSIGN: \"" << Atoms[x->index] << "\" -> " |
|  |  << (Status > 0 ? "True" : "False") << endl; |
|  | this->scheme[x->index] = Status > 0 ? 1 : 2; |
|  | this->Rec\_assign.top().push\_back(x->index); |
|  | for (auto it = x->oc->begin(); it != x->oc->end(); it = it->next()) { |
|  | if ((Status < 0) == it->X->lit->X->neg) |
|  | this->removeClause(it->X->lit->X->cl); |
|  | else { |
|  | this->removeLiteral(it->X->lit->X->cl, it->X->lit); |
|  | if (it->X->lit->X->cl->X->lt->empty()) { |
|  | this->containEmptyClause = true; |
|  | break; |
|  |  } |
|  |  } |
|  |  } |
|  | /***/ cout << "FORMULA: finish assignments:" << endl; |
|  | /***/ cout << this->str(); |
|  |  SIMPLIFICATION: |
|  | if (!disableSimp) { |
|  | while (this->UnitPropagate()) { |
|  |  } |
|  | /***/ cout << "FORMULA: Unit-propagatated:" << endl; |
|  | /***/ cout << this->str(); |
|  | while (this->PureLiteralAssign()) { |
|  |  } |
|  | /***/ cout << "FORMULA: Pure-literal-assigned:" << endl; |
|  | /***/ cout << this->str(); |
|  |  } |
|  | if (this->CL.empty()) { |
|  | /***/ cout << "***FORMULA IS EMPTY: It can be satisfied." << endl; |
|  | /***/ cout << "***ALGORITHM FINISHED." << endl; |
|  | return true; |
|  |  } |
|  | if (this->containEmptyClause) { |
|  | /***/ cout << "***FORMULA CONTAIN EMPTY CLAUSES: backtrack." << endl |
|  |  << endl; |
|  | this->containEmptyClause = false; |
|  | continue; |
|  |  } |
|  |  STACK.push(abs(Status) + 1); |
|  |  STACK.push(-abs(Status) - 1); |
|  | /***/ cout << endl; |
|  |  } |
|  | /***/ cout << "***The formula cannot be satisfied." << endl; |
|  | /***/ cout << "***ALGORITHM FINISHED." << endl; |
|  | return false; |
|  | } |

Code usage examples

Minimum C++ standard: C++ 11

Input format: a positive integer nnn on a line, indicating that the conjunction paradigm contains nnn clauses. Next nnn line, line iii begins with a positive integer kikik_i means the clause contains kikik_i text, followed by kikikik_ I is a space-delimited string representing each text. If the string starts with ^, it means that the text is negative.

For example, the following conjunction paradigms:

∧ ∧ ∧ ∧ (a∨b)(¬a∨¬c)(b∨¬t∨a∨¬c)(c∨d)a(a∨b)∧ (¬a∨¬c)∧ (b∨¬t∨a∨¬c)∧ (c∨d)∧ a\begin{aligned}
&(a\vee b)\
\wedge\ &(\neg a\vee\neg c)\
\wedge\ &(b\vee\neg t\vee a\vee\neg c)\
\wedge\ &(c\vee d)\
\wedge\ &a
\end{aligned}
The input code is:

|  | 5 |
|  | 2 a b |
|  | 2 ^a ^c |
|  | 4 b ^t a ^c |
|  | 2 c d |
|  | 1 a |

Contains the header file dpll.hpp, guaranteed with slist.hpp can create a CNF object and call it in the same folder. The read() method reads the join paradigm from standard input and output. Then you can call the method. DPLL() applies the algorithm (with the parameter true to skip the simplification step), and a lot of debugging information is output together. If you want to get a feasible assignment scheme (provided the formula is satisfied), you can output it after applying the DPLL algorithm. The schemeStr() method generates a string with the following styles:

|  | "a" -> True |
|  | "b" -> \_ |
|  | "c" -> False |
|  | "t" -> \_ |
|  | "d" -> True |

Each row represents the assignment of a variable, if it is underlined_ That means it can be assigned either true or false.

We apply the algorithm to the above sample conjunction paradigm and the output should be:

|  | === NEW STATUS : 0 === |
|  | FORMULA: begin processing(layer=0): |
|  | { |
|  | | 　 ( a ∨ b ) |
|  | | ∧ ( ¬a ∨ ¬c ) |
|  | | ∧ ( b ∨ ¬t ∨ a ∨ ¬c ) |
|  | | ∧ ( c ∨ d ) |
|  | | ∧ a |
|  | } |
|  | INIT: skip assignments |
|  | DEL Clause "a ∨ b" |
|  | DEL literal "¬a" in "¬a ∨ ¬c" |
|  | DEL Clause "b ∨ ¬t ∨ a ∨ ¬c" |
|  | DEL literal "c" in "c ∨ d" |
|  | FORMULA: Unit-propagatated: |
|  | { |
|  | | 　 ¬c |
|  | | ∧ d |
|  | | ∧ a |
|  | } |
|  | DEL Clause "a" |
|  | DEL Clause "¬c" |
|  | DEL Clause "d" |
|  | FORMULA: Pure-literal-assigned: |
|  | { |
|  | } |
|  | ***FORMULA IS EMPTY: It can be satisfied. |
|  | ***ALGORITHM FINISHED. |
|  | 1 |
|  | "a" -> True |
|  | "b" -> \_ |
|  | "c" -> False |
|  | "t" -> \_ |
|  | "d" -> True |

The process of algorithm execution and the content of formula after each simplification step can be clearly seen. A simplification of this formula is sufficient to determine whether it is satisfactory or not. We pass it on. DPLL(true) Disable simplification steps to clearly see the algorithm backtracking process:

|  | === NEW STATUS : 0 === |
|  | FORMULA: begin processing(layer=0): |
|  | { |
|  | | 　 ( a ∨ b ) |
|  | | ∧ ( ¬a ∨ ¬c ) |
|  | | ∧ ( b ∨ ¬t ∨ a ∨ ¬c ) |
|  | | ∧ ( c ∨ d ) |
|  | | ∧ a |
|  | } |
|  | INIT: skip assignments |
|  |  |
|  | === NEW STATUS : -1 === |
|  | FORMULA: begin processing(layer=1): |
|  | { |
|  | | 　 ( a ∨ b ) |
|  | | ∧ ( ¬a ∨ ¬c ) |
|  | | ∧ ( b ∨ ¬t ∨ a ∨ ¬c ) |
|  | | ∧ ( c ∨ d ) |
|  | | ∧ a |
|  | } |
|  | ASSIGN: "a" -> False |
|  | DEL literal "a" in "a ∨ b" |
|  | DEL Clause "¬a ∨ ¬c" |
|  | DEL literal "a" in "b ∨ ¬t ∨ a ∨ ¬c" |
|  | DEL literal "a" in "a" |
|  | FORMULA: finish assignments: |
|  | { |
|  | | 　 b |
|  | | ∧ ( b ∨ ¬t ∨ ¬c ) |
|  | | ∧ ( c ∨ d ) |
|  | | ∧ ( ) |
|  | } |
|  | ***FORMULA CONTAIN EMPTY CLAUSES: backtrack. |
|  |  |
|  | === NEW STATUS : 1 === |
|  | BACKTRACK: -> 0 |
|  | FORMULA: begin processing(layer=1): |
|  | { |
|  | | 　 ( a ∨ b ) |
|  | | ∧ ( ¬a ∨ ¬c ) |
|  | | ∧ ( b ∨ ¬t ∨ a ∨ ¬c ) |
|  | | ∧ ( c ∨ d ) |
|  | | ∧ a |
|  | } |
|  | ASSIGN: "a" -> True |
|  | DEL Clause "a ∨ b" |
|  | DEL literal "¬a" in "¬a ∨ ¬c" |
|  | DEL Clause "b ∨ ¬t ∨ a ∨ ¬c" |
|  | DEL Clause "a" |
|  | FORMULA: finish assignments: |
|  | { |
|  | | 　 ¬c |
|  | | ∧ ( c ∨ d ) |
|  | } |
|  |  |
|  | === NEW STATUS : -2 === |
|  | FORMULA: begin processing(layer=2): |
|  | { |
|  | | 　 ¬c |
|  | | ∧ ( c ∨ d ) |
|  | } |
|  | ASSIGN: "c" -> False |
|  | DEL Clause "¬c" |
|  | DEL literal "c" in "c ∨ d" |
|  | FORMULA: finish assignments: |
|  | { |
|  | | 　 d |
|  | } |
|  |  |
|  | === NEW STATUS : -3 === |
|  | FORMULA: begin processing(layer=3): |
|  | { |
|  | | 　 d |
|  | } |
|  | ASSIGN: "d" -> False |
|  | DEL literal "d" in "d" |
|  | FORMULA: finish assignments: |
|  | { |
|  | | 　 ( ) |
|  | } |
|  | ***FORMULA CONTAIN EMPTY CLAUSES: backtrack. |
|  |  |
|  | === NEW STATUS : 3 === |
|  | BACKTRACK: -> 2 |
|  | FORMULA: begin processing(layer=3): |
|  | { |
|  | | 　 d |
|  | } |
|  | ASSIGN: "d" -> True |
|  | DEL Clause "d" |
|  | FORMULA: finish assignments: |
|  | { |
|  | } |
|  | ***FORMULA IS EMPTY: It can be satisfied. |
|  | ***ALGORITHM FINISHED. |
|  | 1 |
|  | "a" -> True |
|  | "b" -> \_ |
|  | "c" -> False |
|  | "t" -> \_ |
|  | "d" -> True |

The presence of BACKTRACK in the middle of the output indicates that the algorithm performs a backtrace, restoring the formula back to its pre-assignment and simplification form.

Reference resources

• Boolean satisfiability problem - Wikipedia
  https://en.wikipedia.org/wiki/Boolean_satisfiability_problem
• DPLL algorithm - Wikipedia
  https://en.wikipedia.org/wiki/DPLL_algorithm