Divide an array into three parts according to a certain partition value, that is, the part less than the value, equal to the part and greater than the part. This problem is called the Dutch flag problem.
The Dutch flag is composed of three colors, and the problem is to divide the array into three parts. The two are similar, so the problem is named.
Simplified Dutch flag
Consider the simplified version first. Divide an array into two parts, such as the part less than or equal to the partition value and the part greater than. You can think of using double pointers here. The two pointers are the right boundary of the less than or equal area and the traversal time subscript respectively. In this way, the array is divided into three parts: less than or equal area, greater than area and area to be traversed.
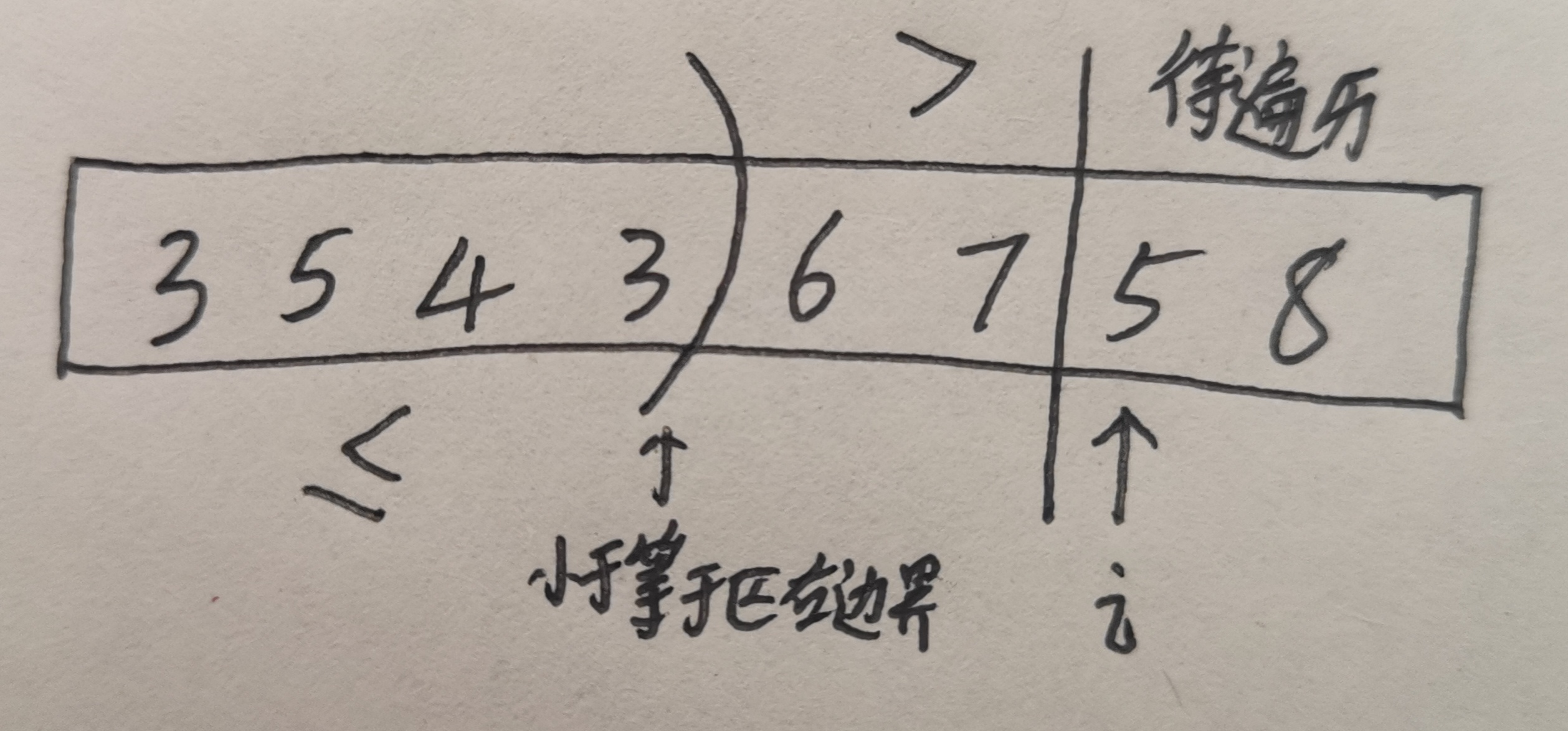
Here, the partition value is taken as 5.
In this way, the less than or equal area pushes the greater than area to traverse backward. When the array traversal is completed, the array division is also completed smoothly.
int flag1(vector<int> &arr)
{
int i=0,small=-1;//Traverse the pointer of the array and the left boundary of the area less than or equal to
int key=arr[0];//Partition value here takes the first value of the array or other values
while(i<arr.size())
{
if(arr[i]<=key)
{
swap(arr[small+1],arr[i]);//Exchange the next number of areas less than or equal to and the number of passes
++small;
}
++i;
}
return 0;
}
Here, the function of swap() is to exchange two numbers, and the code here is omitted.
Dutch flag issue
Now consider dividing the array into three parts. From the above simplified version of the problem, one more pointer is set here to indicate that it is greater than the right boundary of the area. In this way, the array is divided into four parts: less than area, equal to area, area to be traversed and greater than area.
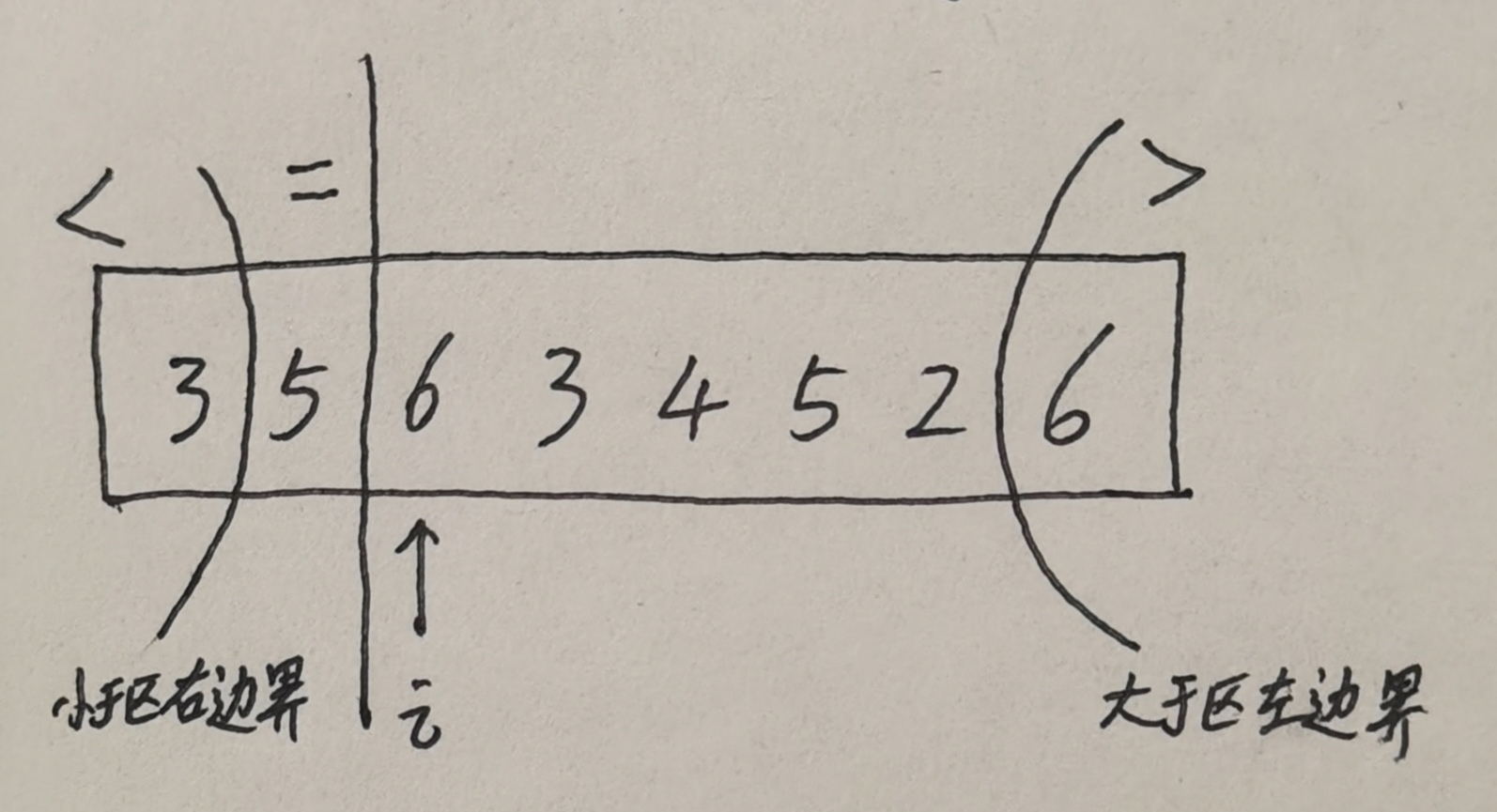
The partition value here is still taken as 5.
In this way, it is equivalent that the less than area pushes the equal area backward, while the greater than area gradually expands to the left. When the array traverses to greater than the area boundary, the array partition is also completed successfully.
int flag2(vector<int> &arr)
{
int i=0,small=-1;//Traverses the pointer of the array and is less than the right boundary of the region
int big=arr.size();//Greater than the left boundary of the region
int key=arr[0];//Partition value here takes the first value of the array or other values
while(i<big)
{
if(arr[i]<key)
{
swap(arr[small+1],arr[i]);//The next number of swap areas and the number of passes
++small;
++i;
}else if(arr[i]==key)
{
++i;
}else
{
swap(arr[big-1],arr[i]);
--big;
}
}
return 0;
}
Quick sort
Quick sort is a widely used sorting algorithm. Its essence is to divide the array with a value in the array as the division value, so as to determine the position of the value, and then recursion or iteration. The Dutch flag is used here.
Quick sort 1.0
The quick sort algorithm in version 1.0 takes the first value in the array as the division value, divides the array into less than or equal to the area and greater than the area, and then exchanges the value with the last value of less than or equal to the area, and puts the value in the last position. Then continue recursion or iteration.
int partition1(vector<int> &arr,int left,int right)
{
if(left>=right)
{
return 0;
}
int i=left,small=left-1;//Traverse the pointer of the array and the left boundary of the area less than or equal to
int key=arr[left];//Partition value here is still the first value of the array
while(i<=right)
{
if(arr[i]<=key)
{
swap(arr[small+1],arr[i]);
++small;
}
++i;
}
swap(arr[left],arr[small]);//Put the partition value at the last position of the area less than or equal to
partition1(arr,0,small-1);
partition1(arr,small+1,right);
}
int qsort1(vector<int> &arr)
{
partition1(arr,0,arr.size()-1);
return 0;
}
Quick sort 2.0
Version 2.0 is different from version 1.0 in that it is divided into an equal zone. The difference between 1.0 and 2.0 is just like the simplified version and official version of the Dutch flag.
int partition2(vector<int> &arr,int left,int right)
{
if(left>=right)
{
return 0;
}
int i=left,small=left-1;//Traverses the pointer of the array and is less than the right boundary of the region
int big=right+1;//Greater than the left boundary of the region
int key=arr[left];
while(i<big)
{
if(arr[i]<key)
{
swap(arr[small+1],arr[i]);//The next number of swap areas and the number of passes
++small;
++i;
}else if(arr[i]==key)
{
++i;
}else
{
swap(arr[big-1],arr[i]);
--big;
}
}
partition2(arr,0,small);
partition2(arr,big,right);
return 0;
}
int qsort2(vector<int> &arr)
{
partition2(arr,0,arr.size()-1);
return 0;
}
Note that when arr[i] is larger than the partition value, the I value remains unchanged.
Version 2.0 is slightly faster than version 1.0 because version 2.0 solves a batch number at a time.
Quick sort 3.0
The biggest drawback of 1.0 and 2.0 is that when the original array is basically ordered, the partition value may be biased, making the time complexity close to O (N2). In order to improve this, we can randomly select the partition value and exchange it with the first value of the original array, which is consistent with versions 1.0 and 2.0.
int partition3(vector<int> &arr,int left,int right)
{
if(left>=right)
{
return 0;
}
int i=left,small=left-1;//Traverse the pointer of the array and the left boundary of the area less than or equal to
int index=left+rand()%(right-left+1);//The partition value randomly extracts a number within the sorting range
swap(arr[index],arr[left]);//Exchange the extracted value with the first value in the range, and then it will be the same as 1.0
int key=arr[left];
while(i<=right)
{
if(arr[i]<=key)
{
swap(arr[small+1],arr[i]);
++small;
}
++i;
}
swap(arr[left],arr[small]);//Put the partition value at the last position of the area less than or equal to
partition3(arr,0,small-1);
partition3(arr,small+1,right);
}
int qsort3(vector<int> &arr)
{
partition3(arr,0,arr.size()-1);
return 0;
}
Note that if it is divided into four parts, you don't have to exchange the randomly selected value with the first value of the array.
int partition4(vector<int> &arr,int left,int right)
{
if(left>=right)
{
return 0;
}
int i=left,small=left-1;//Traverses the pointer of the array and is less than the right boundary of the region
int big=right+1;//Greater than the left boundary of the region
int key=arr[left+rand()%(right-left+1)];
while(i<big)
{
if(arr[i]<key)
{
swap(arr[small+1],arr[i]);//The next number of swap areas and the number of passes
++small;
++i;
}else if(arr[i]==key)
{
++i;
}else
{
swap(arr[big-1],arr[i]);
--big;
}
}
partition4(arr,0,small);
partition4(arr,big,right);
return 0;
}
int qsort4(vector<int> &arr)
{
partition4(arr,0,arr.size()-1);
return 0;
}
In this case, since the partition values are randomly selected, the time complexity is O (Nlog N).
In addition, the spatial complexity of quick sort is O (log N). In versions 1.0 and 2.0, the worst case becomes o (N).
Logarithm
Finally, post the logarithm code
int compare()//Logarithm
{
int times=1;
vector<int> arr1;
for(;times<=TIME_N;++times)
{
for(int i=0;i<LEN;++i)
{
arr1.push_back(rand()&1023);
}
vector<int> arr2(arr1);
qsort3(arr1);
qsort4(arr2);
//Compare two sorted data
if(arr1!=arr2)
{
return times;
}
}
return 0;
}
Different sorting methods can be compared here. If the return value is 0, it indicates that the algorithm is basically OK.