catalogue
Basic dynamic programming: one dimension
Sword finger Offer 10- I. Fibonacci sequence
Sword finger Offer 10- II. Frog jumping steps
Sword finger Offer 63. Maximum profit of stock
Sword finger Offer 42. Maximum sum of continuous subarrays
413. Division of arithmetic sequence
Basic dynamic programming: one dimension

Recursion cannot be used and will timeout.
class Solution {
public:
int fib(int n) {
int mod = 1000000007;
if(n < 2)
{
return n;
}
int first = 0, second =1;
int count;
for(int i = 2;i < n+1;i++)
{
count = (first+second)%mod;
first = second;
second = count;
}
return count;
}
};
The possibility of jumping up N steps is the possibility of N-1 jumping once 1 and N-2 jumping once 2 combined.
class Solution {
public:
int numWays(int n) {
int mod = 1000000007;
if(n == 0 | n == 1)
return 1;
int first = 1;
int second = 1;
int count;
for(int i = 2; i <= n;i++)
{
count = (first + second)%mod;
first = second;
second = count;
}
return count;
}
};
Record a historical lowest price
class Solution {
public:
int maxProfit(vector<int>& prices) {
int inf = 1000000000;
int minprice = inf , maxprice = 0;
for(int pe : prices)
{
maxprice = max(maxprice,pe - minprice);
minprice = min(pe , minprice); //Record a historical lowest price
}
return maxprice;
}
};
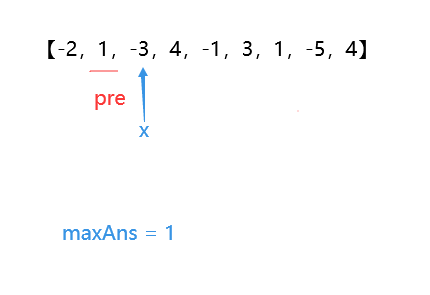
Compare the current value and the sum of its current value + pre, and save it as the current pre
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int pre = 0, maxAns = nums[0];
for(int a : nums)
{
pre = max(pre+a , a);
maxAns = max(pre , maxAns);
}
return maxAns;
}
};
Define an array dp. dp[i] represents the maximum number of houses that can be robbed when robbing the ith house. We consider dp[i]. There are two possibilities for the maximum number of robberies. One is that we choose not to rob the house, and the cumulative amount is dp[i-1]; The other is that we choose to rob this house, so the maximum amount accumulated before can only be dp[i-2], because we can't rob the i-1 house, otherwise the alarm will be triggered. Therefore, the state transition equation of this problem is dp[i] = max(dp[i-1], nums[i-1] + dp[i-2]).
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if(n == 0)
return 0;
vector<int> dp(n+1,0); //Indicates the maximum amount before grabbing the i-th room
dp[1] = nums[0]; //Before we got the first house, it was nums[0]
for(int i = 2;i <= n ;i++)
{
dp[i] = max(dp[i-1],dp[i-2]+nums[i-1]);
//Do not rob the ith house, or rob it and add the current house amount nums[i-1]
}
return dp[n];
}
};class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if(n == 0)
return 0;
int cur = 0;
int pre = 0;
int ppre = 0;
for(int i = 0;i < n ;i++)
{
cur = max(pre , ppre+nums[i]);
ppre = pre;
pre = cur;
}
return cur;
}
};

The subarray must satisfy num[i] - num[i-1] = num[i-1] - num[i-2]. However, because our definition of dp array is usually the number of subarrays that end with I and meet some conditions, and the arithmetic subarray can end at any position, we need to sum the dp array at the end of this problem.
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n = nums.size();
if(n <= 2) return 0;
///End with i
vector<int> dp(n ,0);
for(int i = 2;i < n ;i++)
{
if(nums[i] - nums[i-1] == nums[i-1] - nums[i-2])
{
dp[i] = dp[i-1]+1;
}
}
return accumulate(dp.begin(),dp.end(),0);
//Find the sum of all positions
}
};
Basic dynamic programming: 2D
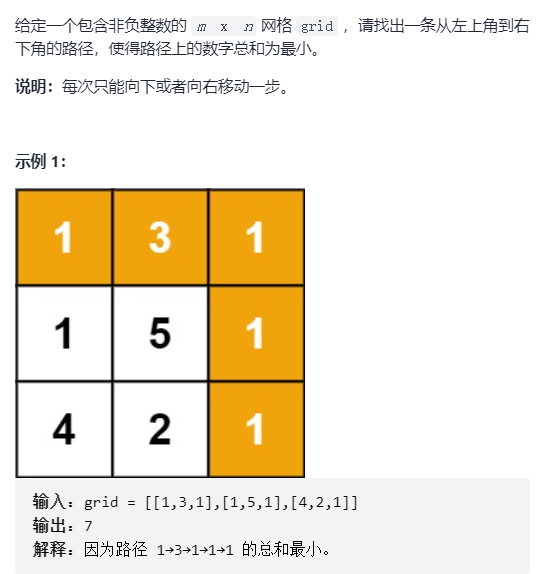
Define a two-dimensional dp array, where dp[i][j] represents the numerical sum of the optimal path from the upper left corner to (i, j). Because we can only move down or right each time, we can easily get the state transition equation dp[i][j] =min(dp[i-1][j], dp[i][j-1]) + grid[i][j], where grid represents the original array.
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(); // m x n
int n = grid[0].size(); //
vector<vector<int>> dp(m,vector<int>(n,0)); //State transition equation: dp represents the shortest path to the position (i, j)
for(int i = 0;i < m;i++)
{
for(int j = 0; j < n; j++)
{
if(i==0 && j==0) dp[i][j] = grid[i][j];
else if(i==0) dp[i][j] = dp[i][j-1] + grid[i][j];
else if(j==0) dp[i][j] = dp[i-1][j] + grid[i][j];
else{
dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
//The value of the current position plus the shortest path to the top or left
}
}
}
return dp[m-1][n-1]; //Returns the shortest path to the lower right corner
}
};

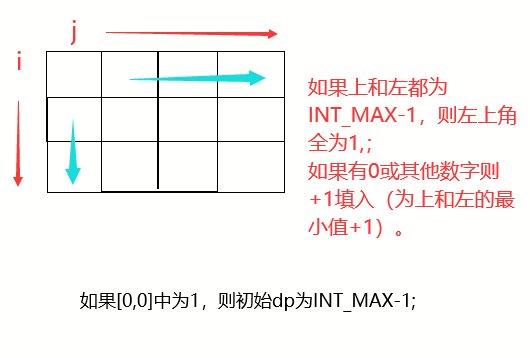

Conduct a dynamic search from top left to bottom right, and then conduct a dynamic search from bottom right to top left to complete the search in four directions.
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int m = mat.size();
int n = mat[0].size();
vector<vector<int>> dp(m,vector(n, INT_MAX-1));
for(int i = 0;i < m;i++)
{
for(int j = 0;j < n;j++)
{
if(mat[i][j] == 0)
{
dp[i][j] = 0;
}
else{
if(i > 0)
{
dp[i][j] = min(dp[i][j] , dp[i-1][j]+1);
}
if(j > 0)
{
dp[i][j] = min(dp[i][j] , dp[i][j-1] + 1);
}
//At this time dp stores INT_MAX-1 and the minimum value of upper and left + 1;
}
}
}//At this time, except for [0,0], the distance should be INT_MAX
for(int i = m-1 ;i >= 0;i--)
{
for(int j = n-1 ;j >= 0;j--)
{
if(mat[i][j] != 0)
{
if( i < m -1)
{
dp[i][j] = min(dp[i][j] ,dp[i + 1][j] + 1);
}
if(j < n - 1)
{
dp[i][j] = min(dp[i][j] ,dp[i][j+1] + 1);
}
} //At this time, dp stores the minimum value of just dp and lower and right + 1.
}
}
return dp;
}
};
//If the solution of the above problem is used, problems will occur when (0,0) is 1

Method 1: violent solution
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
if(m == 0 || n == 0)
{
return 0;
}
int maxSide = 0;
for(int i = 0; i < m ;i++)
{
for(int j = 0;j < n;j++)
{
if(matrix[i][j] == '1') //If you encounter a 1 as the upper left corner of the square
{
maxSide = max(maxSide,1); //Storage maximum
int currentMaxSide = min(m-i,n-j); //Calculates the current maximum possible square side length
for(int k = 1; k < currentMaxSide ;k++)
{
//Determine whether each line in the future is 1
bool flag = true;
if(matrix[i+k][j+k] == '0') //judge
{
break;
}
for(int m = 0;m < k;m++) //Judge whether the new row / column is 1
{
if(matrix[i+k][j+m] == '0' || matrix[i+m][j+k] == '0')
{
flag = false;
break;
}
}
if(flag)
{
maxSide = max(maxSide ,k+1);
}else{
break;
}
}
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
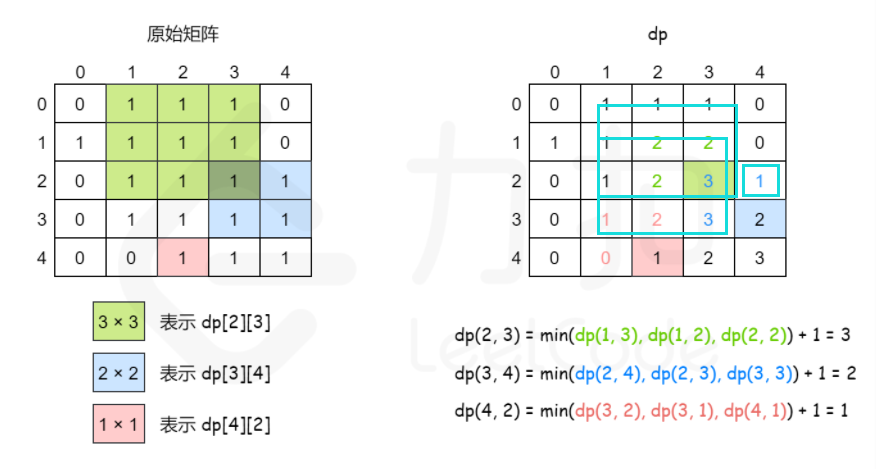
};Method 2: dynamic programming - define a two-dimensional dp array, where dp[i][j] represents the attribute of a square or rectangle with (i, j) as the lower right corner that meets the conditions of the topic.

class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
if(m == 0 || n == 0)
{
return 0;
}
int maxSide = 0;
vector<vector<int>> dp(m,vector<int>(n));
//dp[i][j] indicates that one (i,j) is the positive direction of the lower right corner or the side length of the rectangle
for(int i = 0; i < m;i++)
{
for(int j = 0; j < n;j++)
{
if(matrix[i][j] == '1')
{
if(i == 0||j == 0)
{
dp[i][j] = 1;
}else{
dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]) , dp[i-1][j-1]) + 1;
}
maxSide = max(maxSide,dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
};