1, Interval dp

As the name suggests, interval dp is the problem of solving the optimal value on the interval.

The main idea is to solve the inter cell first, and then use the optimal solution combination between cells to obtain the optimal solution of the maximum interval.

If you don't say much, go straight to the example:

Classic example: (a very classic topic of interval dp): Stone merging

There are n piles of stones in a row, and each pile of stones has a certain amount. Now we need to merge n pairs of stones into a pile. In the process of merging, only two adjacent piles of stones can be merged at a time. The cost of each merging is the sum of the number of two piles of lions. After n-1 merging, it becomes a pile, and the minimum value of the total cost is solved.

For example: [4,1,1,4] - [4,2,4] - [4,6] - [10];

2 + 6 + 10 = 18

Problem solving ideas:

First, when we consider the last merge, we will find that the first heap is merged by the first k heap, while the latter heap is merged by the later n-k heap. The price is the total number of stones.

1. Define status: let dp[i][j] represent the minimum cost of merging heap I to heap j; sum[i][j] is the number of stones combined from pile I to pile j.

2. Transfer equation: dp[i][j]=min(dp[i][j],dp[i][k]+dp[i][n-k]+sum[i][j])

3. Solve the sub state: recursion and recursion can be used. In case of ground deduction, it can be enumerated from short interval to long interval.

4. Complexity O(n^3), state O(n^2).

Code (part):

for(int len=2;len<=n;++len)
    for(int l=1;l+len-1<=n;++l)// len=r-l+1 -> r=l+len-1<=n
    {
        int r=l+len-1;
        for(int k=l;k<r;++k)
            dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]+sum[l][r]);
    }

Interval dp template:

1. Define the state: the state DP(L,R) represents the optimal solution of (L~R)

2. Transfer equation: enumerate interval partition points DP(L,R)=DP(L,K)+DP(K+1,R)+cost(L,R,K)

3. Recursive or recursive solution: recursion is from short interval enumeration to long interval enumeration.

2, Example link

Example 1: dividing polygons

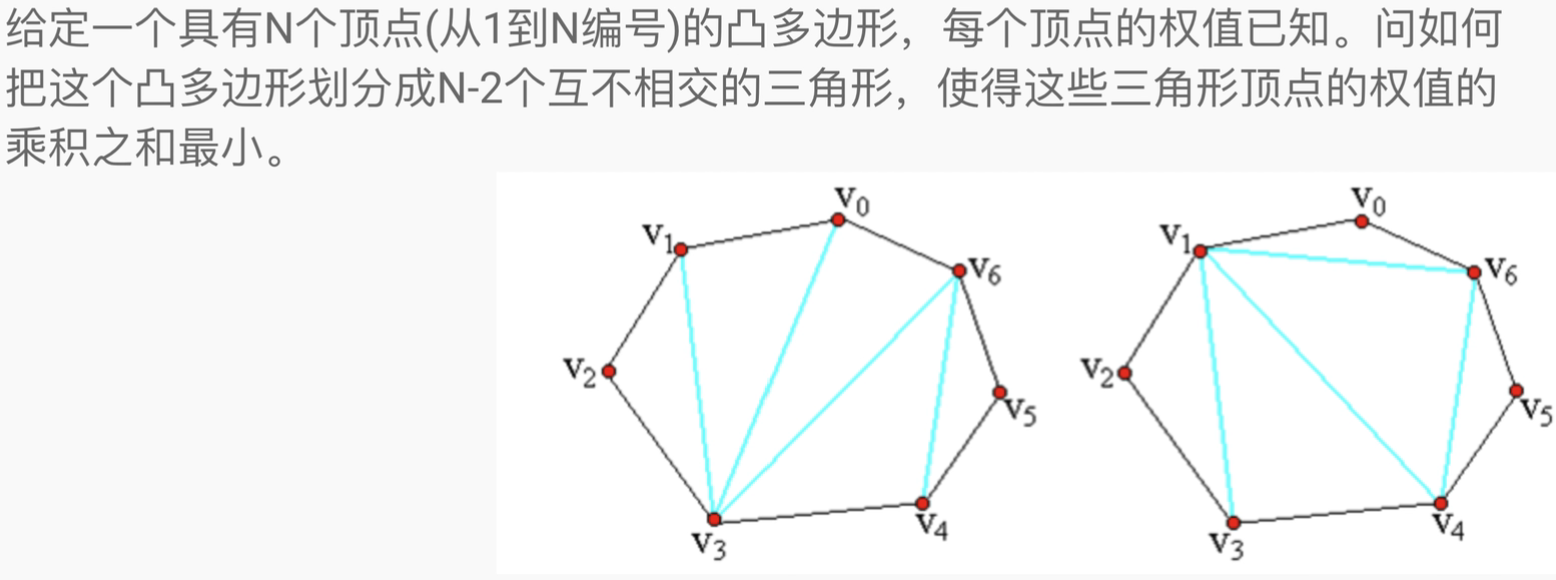
Problem solving ideas:

(copy template)

dp[l][r] represents the minimum value of polygon subdivision composed of l ~ r points.

cost(l ,r ,k)=w[l]*w[k]*w[r].

code:

#include<iostream>
#include<vector>
using namespace std;
int main()
{
	int n;
	cin >> n;
	vector<int> v(n + 1, 0);
	for (int i = 1;i <= n;i++)
		cin >> v.at(i);
	vector<vector<int>> dp(n + 1,vector<int>(n + 1,0));
	for(int len=3;len<=n;len++)
		for (int l = 1;l + len - 1 <= n;l++)
		{
			int r = l + len - 1;
			if (len == 3)
				dp[l][r] = v[l] * v[r] * v[(l + r) / 2];
			for (int k = l+1 ;k+1 < r;k++)
				dp[l][r] =min(dp[l][k+1]+dp[k+1][r]+v[l]*v[r]*v[k+1], dp[l][k] + dp[k][r] + v[l] * v[r] * v[k]);
		}
	cout << dp[1][n];
	return 0;
}

Example 2: Longest palindrome subsequence

Find the length of the longest palindrome subsequence of a sequence

For example: [1,3,2,5,4,2,3,5,1] answer: 7

Problem solving ideas:

Let dp[l][r] represent the length of the longest palindrome subsequence formed by considering only the numbers in the range of l ~ r

if(len==1) dp[l][r]=1;

dp[l][r]=max(dp[l][r-1],dp[l+1][r]);

if(a[l]==a[r]) dp[l][r]=max(dp[l][r],dp[l+1][r-1]+2);

code:

#include<iostream>
#include<vector>
using namespace std;
int main()
{
	int n;
	cin >> n;
	vector<int> v(n + 1, 0);
	vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));
	for (int i = 1;i <= n;i++)
		cin >> v.at(i);
	for(int len=1;len<=n;len++)
		for (int l = 1;len + l - 1 <= n;l++)
		{
			int r = len + l - 1;
			if (len == 1)
				dp[l][r] = 1;
			else
			{
				dp[l][r] = max(dp[l + 1][r], dp[l][r - 1]);
				if (v.at(l) == v[r])
				dp[l][r] = max(dp[l][r], dp[l + 1][r - 1] + 2);
			}
		}
	cout << dp[1][n];
	return 0;
}

Supplement:

The stone sequence in the above stone combination is a chain sequence;

If we consider the ring situation, the combined sequence may be:

Pile i, pile i+1, pile i+2, Pile n, pile 1 Pile i -1;

(the ring is broken from one place and is still chain shaped.)

Suppose we copy the original stone sequence (1,2,3,..., N, 1,2,3,..., n), and the result of interval dp, dp[i][i+n-1] on the new sequence with length of 2n is the result of disconnection from I.

Complexity O(n^3)

Comprehensive training:

[CQOI2007] PAINT_ Niuke Tiba_ Niuke.com (nowcoder.com)

Those who are interested can practice.