1. Introduction to dynamic programming algorithm
Understand dynamic programming ~ know a good article

LeetCode's simple dynamic programming problem:
Summary:
Dynamic programming is not so much an algorithm as a methodology.
The methodology is mainly committed to splitting the "appropriate" problem into three sub objectives, which can be broken at one time:
- 1. Establish the state transition equation
- 2. Cache and reuse previous results
- 3. Calculate from small to large in order
2. "01 backpack" problem
Concept: there are N items and a backpack with a maximum weight of W. The weight of the ith article is weight[i], and the value is value[i]. Each item can only be used once to find out which items are loaded into the backpack and the total value of the items is the largest.
Video link of this case ~ Shang Silicon Valley
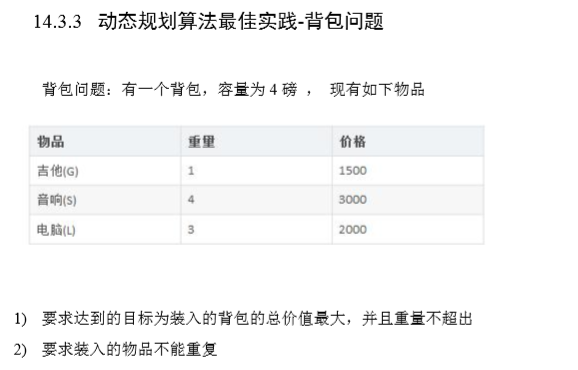
analysis:


Graphic analysis:
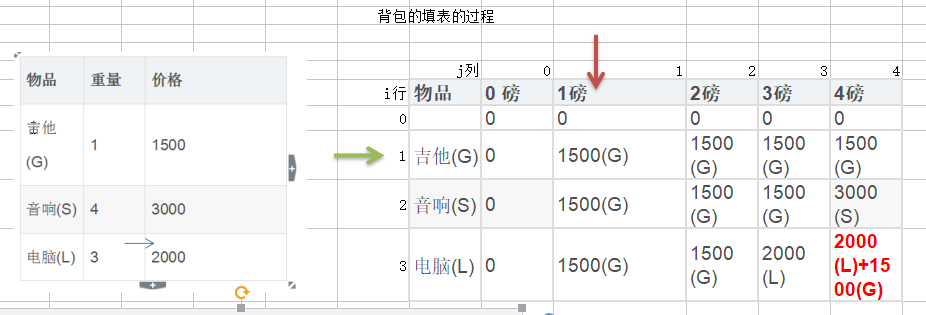
Case study:
1. If there were only guitars now(G) , At this time, no matter how large the backpack capacity is, only one guitar can be put(G)
2. If there is a guitar and stereo, Validation formula:v[1][1] =1500
(1). i = 1, j = 1
(2). w[i] = w[1] = 1 j = 1
v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} :
v[1][1] = max {v[0][1], v[1] + v[0][1-1]} = max{0, 1500 + 0} = 1500
3. If there is a guitar/sound/computer, Validation formula:v[3][4]
(1). i = 3;j = 4
(2). w[i] = w[3] =3 j = 4
j = 4 >= w[i] = 3 => 4 >= 3
v[3][4] = max {v[2][4], v[3] + v[2][1]} = max{3000, 2000+1500} = 2000+1500
induce:
Trace back from the lower right corner of the table. If the value of the best combination of the first n items is the same as that of the first n-1 items, it indicates that the nth item has not been loaded; Otherwise, the nth item is loaded.
Question: what is the maximum value when the backpack capacity is 4?
code:
const w = [1, 4, 3]; //Item weight
const value = [1500, 3000, 2000]; //Value of goods
const m = 4; //Backpack Capacity
const n = 3; //Number of items
// Two dimensional array: v[i][j] represents the maximum value that can be loaded into the backpack with capacity of j in the first I items
let v = new Array(n + 1).fill(0).map(() => new Array(m + 1).fill(0));
for (let i = 1; i <= n; i++) { //i control line
for (let j = 1; j <= m; j++) { //j control column
if (w[i - 1] > j) {
v[i][j] = v[i - 1][j];
} else {
v[i][j] = Math.max(v[i - 1][j], value[i - 1] + v[i - 1][j - w[i - 1]]);
}
}
}
// console.log(v[n][m]); //3500
console.log(v);
// The result of two-dimensional array v is as follows:
// [
// [0, 0, 0, 0, 0],
// [0, 1500, 1500, 1500, 1500],
// [0, 1500, 1500, 1500, 3000],
// [0, 1500, 1500, 2000, 3500]
// ]
Time complexity: O(m*n)
Space complexity: O(m*n)
Optimize the code: reduce the space complexity to O(n).
Two dimensional array becomes one-dimensional array: in one-dimensional dp array, dp[j] means that the value of the items carried by the backpack with capacity of j can be up to dp[j].
const w = [1, 3, 4];
const value = [15, 20, 30];
const n = 4; //Maximum capacity of backpack
const m = w.length; //Number of items
let dp = new Array(n + 1).fill(0);
for (var i = 1; i <= m; i++) {
for (var j = n; j >= w[i - 1]; j--) {
dp[j] = Math.max(dp[j], dp[j - w[i - 1]] + value[i - 1]);
// dp[j]: the current item is not placed -- > because it is in reverse order, it is empty during initialization
// dp[j - w[i - 1]: the maximum value of items that can be loaded in the remaining backpack capacity
// value[i - 1] the value of the current item
}
}
console.log(dp);//[ 0, 15, 15, 20, 35 ]
Key points:
- Inner loop traversal in reverse order (and pay attention to the judgment condition: J > = w [I - 1])
Reason: flashback traversal is to ensure that item i is only put in once! Once it is traversed in positive order, the item will be added multiple times!
- Why can it become a one-dimensional array
Reason: in fact, the layer of dp[i - 1] is copied to dp[i].
Summary of "01 backpack" questions in LeetCode:
- Split equal sum subset : transformed into 0-1 knapsack feasibility problem.
- Goals and objectives: The problem is transformed into the number of 0-1 knapsack schemes.
- Weight of the last stone II: It is transformed into 0-1 knapsack minimum problem.
3. "Complete knapsack" problem
Concept: there are N items and a backpack with a maximum weight of W. the weight of the i-th item is weight[i] and the value is value[i]. Each item has an infinite number (that is, it can be put into the backpack many times). Find out which items are loaded into the backpack and the total value of the items is the largest.
The only difference between complete knapsack and 01 knapsack is that there are unlimited items of each kind.
code:
const w = [1, 3, 4];
const value = [15, 20, 30];
const n = 4; //Maximum capacity of backpack
const m = w.length; //Number of items
let dp = new Array(m + 1).fill(0).map(v => new Array(n + 1).fill(0));
for (var i = 1; i <= m; i++) {
for (var j = 1; j <= n; j++) {
for (var k = 0; k <= j / w[i - 1]; k++) {
if (w[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], k * value[i - 1] + dp[i][j - k * w[i - 1]]);
}
}
}
}
console.log(dp);
// [
// [0, 0, 0, 0, 0],
// [0, 15, 30, 45, 60],
// [0, 15, 30, 45, 60],
// [0, 15, 30, 45, 60]
// ]
Optimization code: reduce the space complexity to O(n). Two dimensional array becomes one-dimensional array
Video link: Complete knapsack problem
- The first way to write:
const w = [1, 3, 4];
const value = [15, 20, 30];
const n = 4; //Maximum capacity of backpack
const m = w.length; //Number of items
let dp = new Array(n + 1).fill(0);
for (var i = 1; i <= m; i++) {
for (var j = n; j >= w[i - 1]; j--) {
for (var k = 0; k <= j / w[i - 1]; k++) {
dp[j] = Math.max(dp[j], dp[j - k * w[i - 1]] + k * value[i - 1]);
}
}
}
console.log(dp);
//[0, 15, 30, 45, 60]
- The second way to write (recommended)
const w = [1, 3, 4];
const value = [15, 20, 30];
const n = 4; //Maximum capacity of backpack
const m = w.length; //Number of items
let dp = new Array(n + 1).fill(0);
for (var i = 1; i <= m; i++) {
for (var j = w[i - 1]; j <= n; j++) {
dp[j] = Math.max(dp[j], dp[j - w[i - 1]] + value[i - 1]);
}
}
console.log(dp);
//[0, 15, 30, 45, 60]
Key points for the second writing method:
- The inner loop becomes forward traversal
- The recurrence equation is completely consistent with 01