Simple dynamic programming

Explanation: dynamic programming (DP) is effective in finding the optimal solutions of many overlapping subproblems. It recombines the problems into subproblems. In order to avoid solving these subproblems many times, their results are gradually calculated and saved, from the simple problem to the whole problem.
Dynamic programming and other traversal algorithms (breadth search) divide the original problem into multiple subproblems and then solve them. The essential difference is that dynamic programming saves the solution of subproblems and avoids repeated calculation. The key to solving dynamic programming is to find the transfer equation, so that we can solve the final problem by calculating and storing the solution of subproblems.

1. Basic dynamic programming: one dimension

Topic 1: given n steps, you can take one or two steps at a time. Find out how many ways you can complete these steps.
For example, the input is a number indicating the number of steps; Output is the total way to climb steps.

This is a very classic Fibonacci sequence problem. Define an array dp, dp[i] represents the number of methods to the i-th order. because
We can take one or two steps at a time, so order i can reach from order i-1 or i-2. In other words, go to step i
The number of methods is the number of methods that go to order i-1 plus the number of methods that go to order i-2. So we get the state transition equation
dp[i] = dp[i-1] + dp[i-2]. Pay attention to the treatment of boundary conditions.

int climbStairs(int n)
{
    if(n<=2) return n;
    vector<int>dp(n+1,1);
    for(int i=2;i<=n;++i)
    {
        dp[i]=dp[i-1]+dp[i-1];
    }
    return dpp[n];
}

Further, we can compress the space of dynamic programming. Because dp[i] is only related to dp[i-1] and dp[i-2], so
Only two variables can be used to store dp[i-1] and dp[i-2], so that the original O(n) space complexity is optimized to O(1) complexity.

int climbStairs(int n)
{
    if(n<=2) return n;
    int pre2=1,pre1=2,cur;
    for(int i=2;i<n;++i)
    {
        cur=pre1+pre2;
        pre2=pre1;
        pre1=cur;
    }
    return cur;
}

Topic 2:

int rob(vector<int>&nums)
{
    if(nums.empty()) return 0;
    int n=nums.size();
    if(n==1) return nums[0];
    int pre2=0,pre1=0,curr;
    for(int i=0;i<n;i++)
    {
        cur=max(pre2+nums[i],pre1);
        pre2=pre1;
        pre1=cur;
    }
    return cur;
}

Topic 3:

int numberOfAirthmeticSlices(vector<int>&nums)
{
    int n=nums.size();
    if(n<3) return 0;
    vector<int>dp(n,0);
    for(int i=2;i<n;++i)
    {
        if(nums[i]-nums[i-1]==nums[i-1]-nums[n-2])
        {
            dp[i]=dp[i-1]+1;
        }
    }
    return accumulate(dp.begin(),dp.end(),0);
}

2. Basic dynamic planning: two-dimensional

Topic 1: given an m × n-size nonnegative integer matrix, find the sum of numbers from the upper left corner to the lower right corner
Small path. You can only move right or down at a time.

We can define a two-dimensional dp array, where dp[i][j] represents the shortest distance from the upper left corner to the position (i, j)
The numerical sum of the optimal path. Because we can only move down or right at a time, we can easily get the state transition equation
dp[i][j] =min(dp[i-1][j], dp[i][j-1]) + grid[i][j], where grid represents the original array.

int minPathSum(vector<vector<int>>&grid)
{
    int m=grid.size();
    int n=grid[0].size();
    vector<vector<int>>dp(m,vector<int>(n,0));
    for(int i=0;i<m;++i)
    {
        for(int j=0;j<n;++j)
        {
            if(i==0&&j==0){
                dp[i][j]=grid[i][j];
            }
            else if(i==0)
            {
                dp[i][j]=dp[i][j-1]+grid[i][j];
            }
            else if(j==0)
            {
                dp[i][j]=dp[i-1][j]+grid[i][j];
            }
            else
            {
                dp[i][j]=min(dp[i-1][j],dp[i][j-1]+grid[i][j];
            }
        }
    }
    return dp[m-1][n-1];
}

Topic 2:

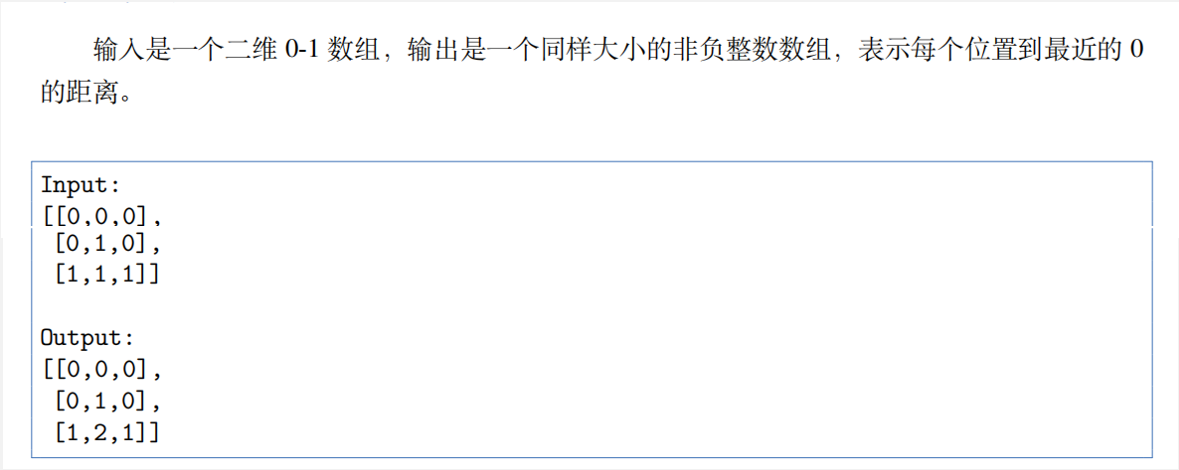
We conduct a dynamic search from top left to bottom right, and then conduct a dynamic search from bottom right to top left. Two dynamic searches can complete the search in four directions.

vector<vector<int>>updateMatrix(vector<vector<int>>&matrix)
{
    if(matrix.empty()) return{};
    int n=matrix.size(),m=matix[0].size();
    vector<vector<int>>dp(n,vector<int>(m,INT_MAX-1));
    for(int i=0;i<n;++i)
    {
        for(int j=0;j<m;++j)
        {
            if(matrix[i][j]==0)
            {
                dp[i][j]=0;
            }
            else
            {
                if(j>0){
                    dp[i][j]=min(dp[i][j],dp[i][j-1]+1);
                }
                if(i>0){
                    dp[i][j]=min(dp[i][j],dp[i-1][j]]+1);
                }
            }
        }
    }
    for(int i=n-1;i>=0;--i)
    {
        for(int j=m-1;j>=0;--j)
        {
            if(matrix[i][j]!=0)
            {
                if(j<m-1)
                {
                    dp[i][j]=min(dp[i][j],dp[i][j]+1);
                }
                if(i<n-1)
                {
                    dp[i][j]=min(dp[i][j],dp[i+1][j]+1);
                }
            }
        }
    }
    return dp;
}

Topic 3:


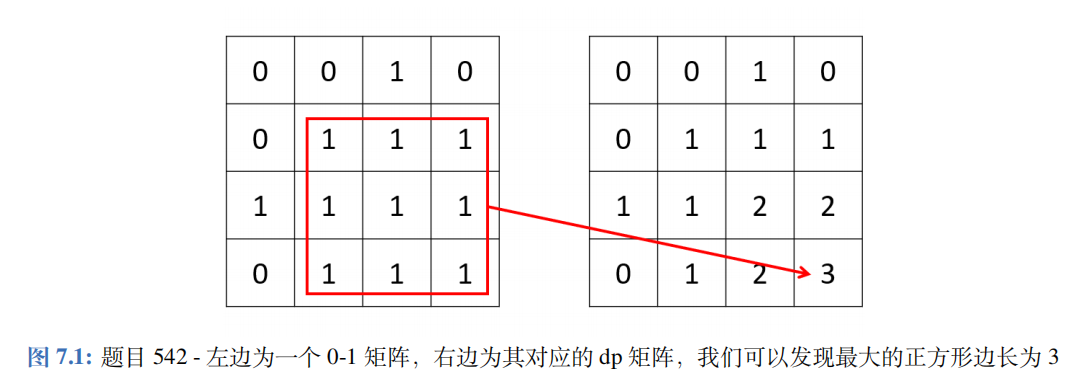
A common way to search for a square or rectangle in a matrix is to define a two-dimensional dp array, where
dp[i][j] represents the attribute of a square or rectangle with (i, j) as the lower right corner that meets the conditions of the topic. For this question, it means
The largest square area composed of 1 with (i, j) as the lower right corner. If the current position is 0, dp[i][j] is 0; If
The current position is 1. We assume that dp[i][j] = k^2. The sufficient condition is that the values of dp[i-1][j-1], dp[i][j-1] and dp[i-1][j] must be
Not less than (k − 1) ^ 2, otherwise the position (i, j) cannot form a square with side length k. Similarly, if one of these three values
If the minimum value of (i, j) is k − 1, then the position of (i, j) is certain and the maximum can form a square with side length K.

int maximalSquare(vector<vector<char>>&matrix)
{
    if(matrix.empty()||matrix[0].empty())
    {
        return 0;
    }
    int m=matrix.size(),n=matrix[0].size(),max_side=0;
    vector<vector<int>>dp(m+1,vector<int>(n+1,0);
    for(int i=1;i<=m;++i)
    {
        for(int j=1;j<=n;++j)
        {
            if(matrix[i-1][j-1]=='1')
                dp[i][j]=min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j]))+1;
            }
            max_side=max(max_side,dp[i][j]);
        }
    }
    return max_side*max_side;
}