Dynamic Programming Principle and LeetCode Solution

Backtrace algorithm implementation-Define state-Draw recursive tree-Find duplicate subproblems-Draw state transition table-Fill tables based on recursive relationships

0-1 Backpack Problem: We have a backpack with a total carrying weight of Wkg. Now we have n items, each of which has a different weight and is inseparable. We now expect to select several items to load into the backpack. How can we maximize the total weight of the items in the backpack without exceeding the weight that the backpack can carry?

We use a two-dimensional array states[n][w+1] to record the status of n items in a wkg backpack.

The weight of the 0th item (subscript number from 0) is 2, either loaded in the backpack or not. After the decision is made, the total weight of the item in the backpack is 0 or 2. We use states[0][0]=true and states[0][2]=true to indicate these two states.

The weight of the first item is also 2. Based on the previous backpack status, there are three different states after this item decision is made. The total weight of the items in the backpack is 0 (0+0), 2(0+2 or 2+0), 4 (2+2). We use states[1][0]=true, states[1][2]=true, states[1][4]=true to represent these three states.

And so on, until you've looked at all the items, the entire states status array is calculated. I've drawn the entire calculation and you can see. Figure 0 is false, and figure 1 is true. We just need to find the closest w value to true on the last level, which is the maximum total weight of the items in the backpack.

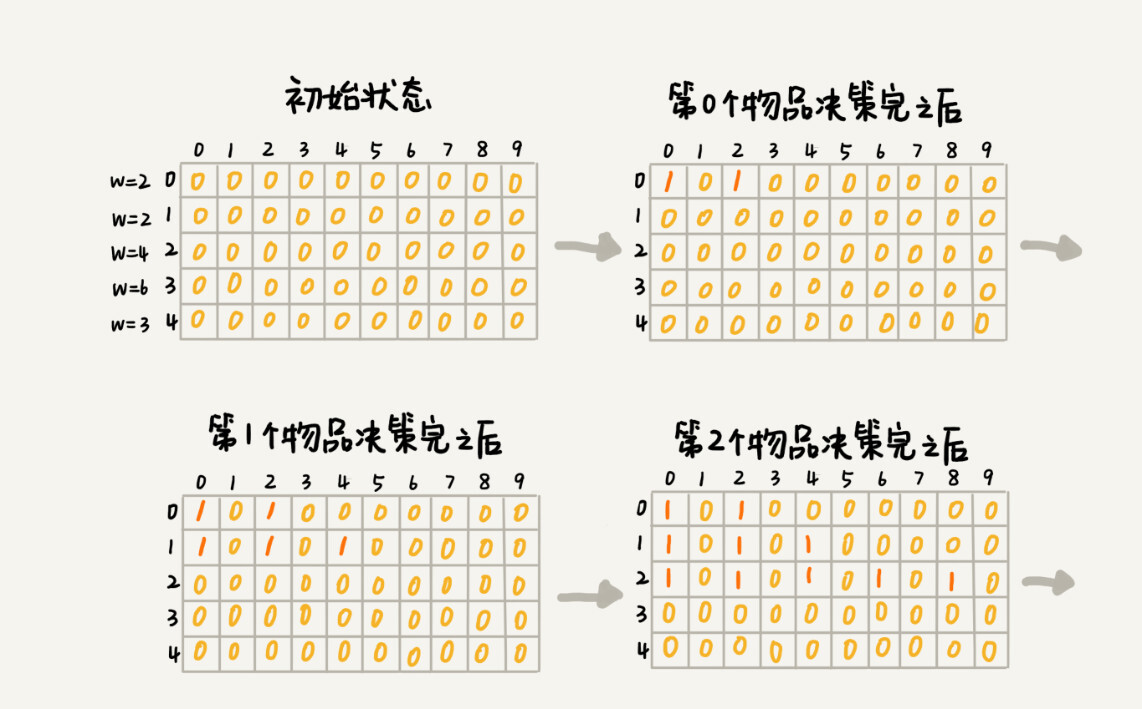
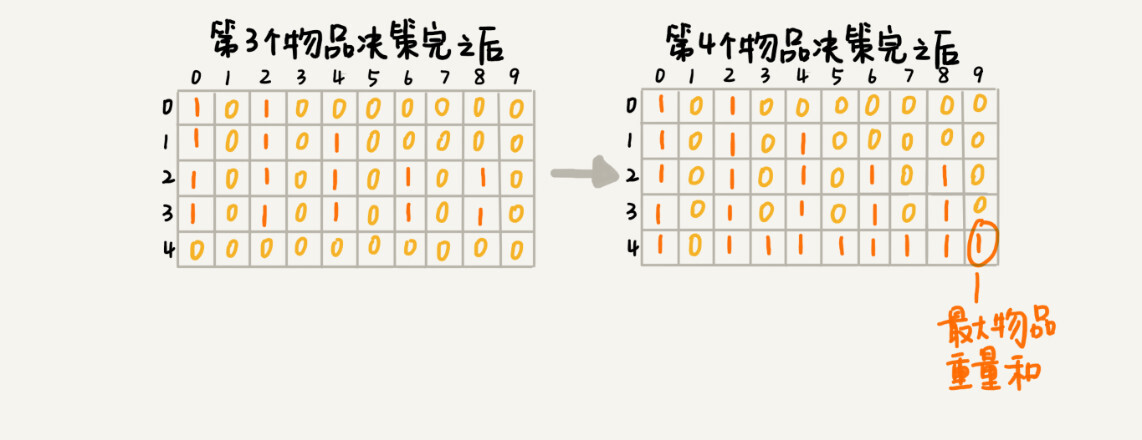
Derive the recursive relationship from the state transition table above and write out the dynamic programming code

weight:Item weight, n:Number of items, w:Backpack can carry weight
public int knapsack(int[] weight, int n, int w) {
  boolean[][] states = new boolean[n][w+1]; // Default value false
  states[0][0] = true;  // The first row of data needs special processing and can be optimized using Sentinel
  if (weight[0] <= w) {
    states[0][weight[0]] = true;
  }
  for (int i = 1; i < n; ++i) { // Dynamic Planning State Transition
    for (int j = 0; j <= w; ++j) {// Don't put item i I in your backpack
      if (states[i-1][j] == true) states[i][j] = states[i-1][j];
    }
    for (int j = 0; j <= w-weight[i]; ++j) {//Put item i I in your backpack
      if (states[i-1][j]==true) states[i][j+weight[i]] = true;
    }
  }
  for (int i = w; i >= 0; --i) { // Output Results
    if (states[n-1][i] == true) return i;
  }
  return 0;
}

2.State Transfer Equation Method

Find Optimal Substructure-Write State Transfer Equation-Translate State Transfer Equation into Code

3.LeetCode Solutions

3.1 LeetCode 509.Fibonacci Number

For example, with a Fibonacci sequence, it is easy to know that his state transfer equation is f(n)=f(n-1)+f(n-2). Recursive implementation is as follows:

int fib(int n) {
	if(n<=1)
		return n;
	return fib(n-1)+fib(n-2);
}

F(n-1) and f(n-2) need to be calculated before f(n), but f(n-1) and f(n-3) need to be calculated.Calculating f(n-2) requires calculating f(n-3) and f(n-4). This recursive derivation involves a large number of repetitive calculations with a time complexity of O(n!).

Repeated subproblems are just the repetitive subproblems to be solved by dynamic planning and are suitable for dynamic planning.Dynamic planning implementation:

int fib(int n) {
	if(n<=1)
		return n;
	vector<int> dp(n+1);
	dp[0] = 0;
	dp[1] = 1;
	for(int i = 2; i <= n; i++) {
		dp[i] = dp[i-1] + dp[i-2];
	}
	return dp[n];
}

This implementation uses dynamic programming, where the optimal solution of the problem contains the optimal solution of the subproblem (the optimal substructure), each step of which relies only on the previous step (no aftereffect) and no duplicate calculation (resolving duplicate subproblems). The time complexity of this algorithm is O(n), but the space complexity is O(n). An O(n) can be written out for general dynamic programming problems.The size of the state transition equation, but most problems can be converted to O(1) space because we only need the state of the previous step and the current state.

int fib(int n) {
	if(n<=1)
		return n;
	int a1 = 0, a2 = 1;
	int res = 0;
	for(int i = 2; i <= n; i++) {
		res = a1+a2;
		a1 = a2;
		a2 = res;
	}
	return res;
}

The above algorithm uses dynamic programming to implement O(n) with time complexity and space complexity O(1).

3.2 LeetCode 70.Climb stairs

int climbStairs(int n) {
	if(n<=2)
		return n;
	int a1 = 1, a2 = 2;
	int res = 0;
	for(int i = 3; i <= n; i++) {
		res = a1+a2;
		a1 = a2;
		a2 = res;
	}
	return res;
}

After summarizing, the current state transfer equation is also f(n) = f(n-1)+f(n-2), just pay attention to the initial state f(1)=1,f(2)=2

3.3 LeetCode 198.Raid homes and plunder houses

int rob(vector<int>& nums) {
	if(nums.size() == 1)
		return nums[0];
	if(nums.size() == 2)
		return max(nums[0], nums[1]);
	int a1 = nums[0];
	int a2 = max(nums[0], nums[1]);
	int an = 0;
	for (int i = 2; i < nums.size(); ++i) {
		an = max(a1+nums[i],a2);
		a1 = a2;
		a2 = an;
	}
	return an;
}

The state transfer equation f(n) = max(f(n-2)+num[n], f(n-1))

3.4 LeetCode 53.Maximum Subordinate Sum

int maxSubArray(vector<int>& nums) {
	int maxCur = nums[0], maxRes = nums[0];
	for (int i = 1; i < nums.size(); ++i) {
		maxCur = max(maxCur+nums[i], nums[i]);
		maxRes = max(maxRes, maxCur);
	}
	return maxRes;
}

The state transfer equation f(n) = max(f(n)+num[i], num[i];(

3.5 LeetCode 152.Product Maximum Subarray

int maxProduct(vector<int>& nums) {
	int maxCur = nums[0];
	int minCur = nums[0];
	int maxRes = nums[0];
	for(int i = 1; i < nums.size(); i++){
		int mx = maxCur, mn = minCur;
		maxCur = max(mx*nums[i], max(nums[i], mn*nums[i]));
		minCur = min(mn*nums[i], min(nums[i], mx*nums[i]));
		maxRes = max(maxCur, maxRes);
	}
	return maxRes;
}

3.6 LeetCode 1014.Best combination for sightseeing

int maxScoreSightseeingPair(vector<int>& values) {
	int maxSum = values[0], maxRes = 0;
	for (int i = 1; i < values.size(); ++i) {
		maxRes = max(maxRes, maxSum+values[i]-i);
		maxSum = max(maxSum, values[i]+i);
	}
	return maxRes;
}

3.7 LeetCode 55.Jump Game

bool canJump(vector<int>& nums) {
	if(nums.size()==1)
		return true;

	int maxIndex{};
	for (int i = 0; i < nums.size()-1;i++) {
		maxIndex = max(maxIndex, i+nums[i]);
		if(maxIndex < i+1)
			return false;
	}
	return true;
}

The state transfer equation f(n) = max(f(n), i+num[i];(

Keywords: Algorithm data structure leetcode Dynamic Programming

Added by mentalfloss on Fri, 10 Sep 2021 08:19:02 +0300

Programming VIP