1. Stair climbing: there are n stairs in total. You can only climb 1 or 2 stairs at a time. How many methods are there to climb n stairs?

Idea: assuming there are 10 stairs in total, when completing the 9th stair, you can complete the 10th stair by going up one step. When the 8th stair is completed, it can also be completed by going up the 2nd stair (if you go up the 1st stair, you will come to the 9th stair, which has been included in the completion of the 9th stair). Therefore, the method F(10) of ascending 10 stairs is equal to the method of ascending 8 stairs plus the method of ascending 9 stairs, that is, F(10) = F(9) + F(8).

class Solution:
    def Step_up_re(self, n):    # Recursive Method 
        if n == 1:
            k = 1
        elif n == 2:
            k = 2
        else:
            k = self.Step_up_re(n-1) + self.Step_up_re(n-2)
        return k

    def Step_up_de(self, n):    # Bottom up derivation
        ways = [1, 2]
        if n > 2:
            for i in range(2,n):
                ways.append(ways[i-1] + ways[i-2])
        return ways[n-1]

2. Find the maximum sum of subarrays in an array.

Idea: find the maximum sum of sub arrays of array arr(10) = [-4, 3, 5, -5, 4, 4, 4, 5, -5, -5, 5]. Assuming that S(n) is the sum of the first n elements, the efficiency of the original problem may be less than max(S(9), S(9)+(-5)). This is solved using recursion from top to bottom. Similarly, we can deduce the solution from bottom to top. That is, starting from the second element in the ARR, judge the maximum element that can be obtained at this position. Gradually deduce backward.

class Solution:
    def max_sub_sum_re(self, str_num, n, max_str):  # Recursive Method 
        """
        :param str_num: Array to be found
        :param n: Array maximum coordinates
        :param max_str: corresponding str_num The maximum value that can be obtained for the element in
        :return: max_str,Namely str_num An array of maximum values that can be evaluated for each element in.
        """
        if n == 0:
            max_sum = str_num[0]
        else:
            max_sum = max(str_num[n], str_num[n] + self.max_sub_sum_re(str_num, n - 1, max_str)[-1])
        max_str.append(max_sum)
        return max(max_str)

    def max_sub_sum_de(self, str_num):  # Bottom up derivation
        len_str = len(str_num)
        max_str = [0 for _ in range(len_str)]
        max_str[0] = str_num[0]
        max_num = max_str[0]
        start, end = 0, 0
        flag = 0            # The start position of the array used to represent the current calculated sum
        if len_str == 1:
            return max_num, str_num[start: end + 1]
        else:
            for i in range(1, len_str):
                if max_str[i-1] > 0:
                    max_str[i] = max_str[i-1] + str_num[i]
                else:
                    flag = i
                    max_str[i] = str_num[i]
                if max_str[i] > max_num:
                    max_num = max_str[i]
                    start = flag
                    end = i
            return max_num, str_num[start: end + 1]

3. Steel bar cutting problem: there is a section of steel bar with length n, and different lengths correspond to different prices, for example: p = [0,1,5,8,9,10,17,17,20,24,30], the subscript of the array is the cutting length, and the array element is the price corresponding to the length. Ask how to cut the steel bar to get the maximum benefit.

Idea: assuming that the price of steel bar with length n is V(n) and the maximum income is S(n), then S(n)=max(V(n),V(1)+max(V(n-1)),V(2)+max(V(n-2))...). Therefore, it can be calculated from top to bottom recursively. Similarly, we can also find the maximum benefit for each length n from bottom to top.

class Solution:
    def cut_rod_re(self, str_num, n):  # Recursive Method 
        if n == 0:
            val = 0
        else:
            val = str_num[n]
            for i in range(1,n):
                val = max(val,str_num[i] + self.cut_rod_re(str_num,n-i))
        return val

    def cut_rod_de(self,str_num, n):    # Bottom up derivation
        max_val = [0 for _ in range(n+1)]
        cut_val = [0 for _ in range(n+1)]   # The length of the left cut at the time of maximum return
        for i in range(1,n+1):
            val = str_num[i]
            for j in range(1,i):
                if max_val[j] + max_val[i-j] > val:
                    val = max_val[j] + max_val[i-j]
                    cut_val[i] = j
            max_val[i] = val
        cut_ways = []   # Record the cutting method
        while True:
            if cut_val[n] == 0:
                cut_ways.append(n)
                break
            else:
                cut_ways.append(cut_val[n])
                n -= cut_val[n]
        return max_val[-1], cut_ways

3. Longest common subsequence: subsequences are not required to be continuous.

Idea:

Therefore, we can recurse gradually from top to bottom.

Similarly, we can build dp from the bottom up_ Table. dp_ The establishment principle of table is: when two elements are the same, its value is equal to the value of the upper left corner plus 1. If they are not equal, its value is equal to the greater of the upper and left values.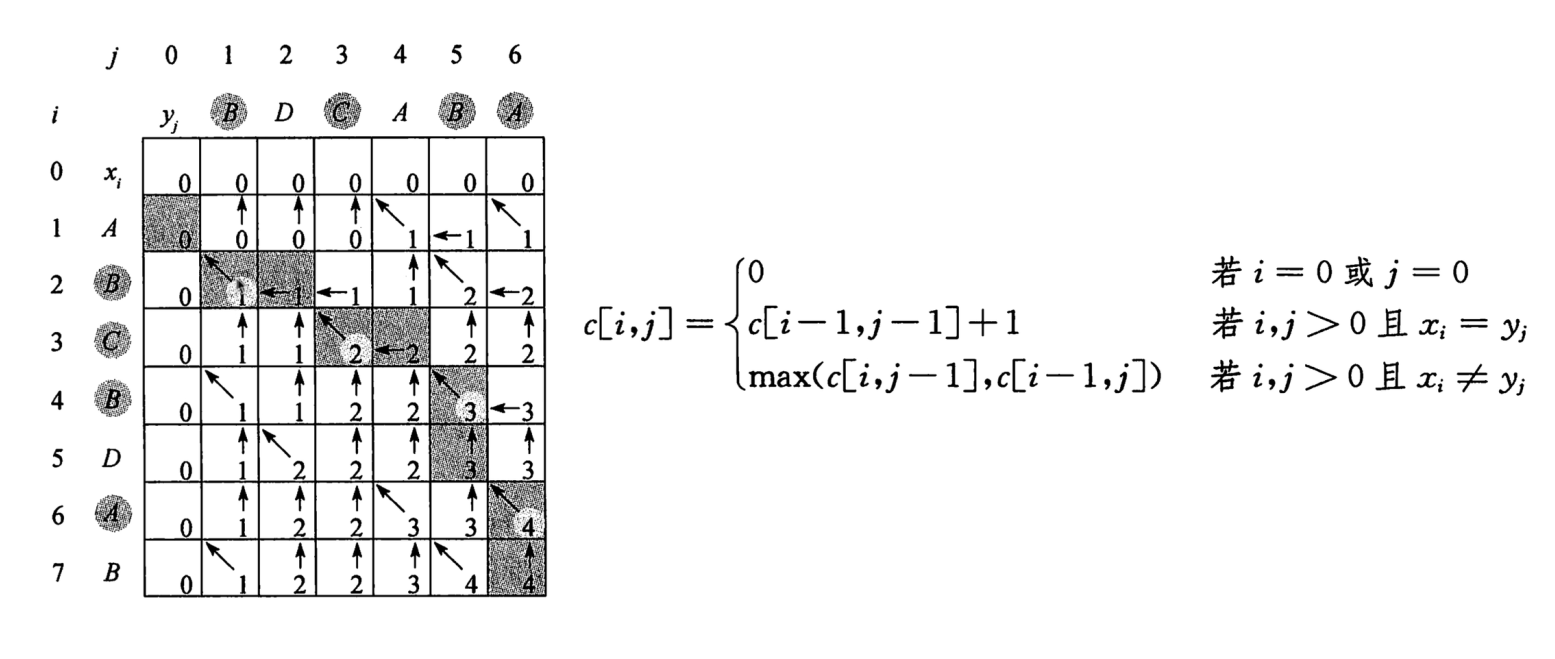

 

class Solution:
    def LCS_re(self, str_A, str_B, len_A, len_B):  # Recursive Method 
        if len_A and len_B:
            if str_A[len_A-1] == str_B[len_B-1]:
                lcs = self.LCS(str_A, str_B, len_A-1, len_B-1)
                lcs += 1
                return lcs
            else:
                lcs = max(self.LCS(str_A, str_B, len_A-1, len_B),self.LCS(str_A, str_B, len_A, len_B-1))
                return lcs
        else:
            lcs = 0
            return lcs

    def LCS_de(self, str_A, str_B):     # Bottom up recursion
        len_A = len(str_A)
        len_B = len(str_B)
        dp_table = [[0 for _ in range(len_A+1)] for _ in range(len_B+1)]
        for i in range(1,len_B+1):
            for j in range(1,len_A+1):
                if str_A[j-1] == str_B[i-1]:
                    dp_table[i][j] = dp_table[i-1][j-1]+1
                else:
                    dp_table[i][j] = max(dp_table[i - 1][j],dp_table[i][j-1])

        i = len_B
        j = len_A
        lcs = [0 for _ in range(dp_table[len_B][len_A])]
        while i > 0 and j > 0:
            if str_B[i-1] == str_A[j-1]:
                lcs[dp_table[i][j]-1] = str_B[i-1]
                i -= 1
                j -= 1
            else:
                if dp_table[i-1][j] >= dp_table[i][j-1]:
                    i -= 1
                else:
                    j -= 1
        return lcs

4. Longest common substring: the substring shall be continuous.

Idea: similar to finding common subsequences, maintaining dp_table, we only need to focus on str_ A[j-1] == str_ DP at B [I-1]_ Whether table [I-1] [J-1] is greater than 0. If it is greater than 0, add 1. If it is equal to 0, set 1. Finally, we just need to focus on DP_ The maximum value in table is the length of the longest common substring.

class Solution:
    def LCS_de(self, str_A, str_B):     # Bottom up recursion
        len_A = len(str_A)
        len_B = len(str_B)
        dp_table = [[0 for _ in range(len_A+1)] for _ in range(len_B+1)]
        len_lcs = 0
        n = 0
        for i in range(1,len_B+1):
            for j in range(1,len_A+1):
                if str_A[j-1] == str_B[i-1]:
                    if dp_table[i-1][j-1] > 0:
                        dp_table[i][j] = dp_table[i-1][j-1]+1
                    else:
                        dp_table[i][j] = 1
                    if dp_table[i][j] > len_lcs:
                        len_lcs = dp_table[i][j]
                        n = i
        lcs = str_B[n - len_lcs:n]
        return lcs,len_lcs

5. Find the longest palindrome subsequence and longest palindrome substring of an array.

Idea: the same as finding the longest common subsequence and the longest common substring, another array is the inversion of the array.